Dimensional Analysis

DIMENSIONAL ANALYSIS

PRE REQUEST DISCUSSION

This Page deals with dimensional analysis,models and similitude,and application of dimensionless parameters.

Many important engineering problems cannot be solved completely by theoretical or mathematical methods. Problems of this type are especially common in fluid-flow, heat-flow, and diffusional operations. One method of attacking a problem for which no mathematical equation can be derived is that of empirical experimentations.

For example, the pressure loss from friction in a long, round, straight, smooth pipe depends on all these variables: the length and diameter of the pipe, the flow rate of the liquid, and the density and viscosity of the liquid. If any one of these variables is changed, the pressure drop also changes. The empirical method of obtaining an equation relating these factors to pressure drop requires that the effect of each separate variable be determined in turn by systematically varying that variable while keep all others constant. The procedure is laborious, and is difficult to organize or correlate the results so obtained into a useful relationship for calculations.

There exists a method intermediate between formal mathematical development and a completely empirical study. It is based on the fact that if a theoretical equation does exist among the variables affecting a physical process, that equation must be dimensionally homogeneous. Because of this requirement it is possible to group many factors into a smaller number of dimensionless groups of variables. The groups themselves rather than the separate factors appear in the final equation.

Concepts

Dimensional analysis drastically simplifies the task of fitting experimental data to design equations where a completely mathematical treatment is not possible; it is also useful in checking the consistency of the units in equations, in converting units, and in the scale-up of data obtained in physical models to predict the performance of full-scale model. The method is based on the concept of dimension and the use of dimensional formulas.

Dimensional analysis does not yield a numerical equation, and experiment is required to complete the solution of the problem. The result of a dimensional analysis is valuable in pointing a way to correlations of experimental data suitable for engineering use.

METHODS OF DIMENSIONAL ANALYSIS

If the number of variables involved in a physical phenomenon are known, then the relation among the variables can be determined by the following two methods.

1.Rayleigh’s method

2. Buckingham’s π  theorem

1Rayleigh’s method

This method is used for determining the expression for a variable which depends upon maximum three or four variables only. If the number of independent variables becomes more than four then it is very difficult to find the expression for the dependent variable.

2 Buckingham’s π theorem.

If  there  are  n  variables  (independent  and  dependent  variables)  in  a  physical

phenomenon and if these variables contain m fundamental dimensions (M, L, T), then the variables are arranged into (n-m) dimensionless numbers. Each term is called Buckingham’s

π  theorem.

Applications

v It is used to justify the dependency of one variable with the other.

v Usually this type of situation occurs in structures and hydraulic machines.

v To solve this problem efficiently, an excellent tool is identified called dimensional analysis.

SMILITUDE –TYPES OF SIMILARITIES

Similitude is defined as the similarity between the model and its prototype in every respect, which means that the model and prototype are completely similar. Three types of similarities must exist between the model and prototype.

Concepts

Whenever it is necessary to perform tests on a model to obtain information that cannot be obtained by analytical means alone, the rules of similitude must be applied. Similitude is the theory and art of predicting prototype performance from model observations

1. Geometric similarity refers to linear dimensions. Two vessels of different sizes are geometrically similar if the ratios of the corresponding dimensions on the two scales are the same. If photographs of two vessels are completely super-impossible, they are geometrically similar.

2.Kinematic similarity refers to motion and requires geometric similarity and the same ratio of velocities for the corresponding positions in the vessels.

3.Dynamic similarity concerns forces and requires all force ratios for corresponding positions to be equal in kinematically similar vessels.

SIGNIFICANCE

The requirement for similitude of flow between model and prototype is that the significant dimensionless parameters must be equal for model and prototype

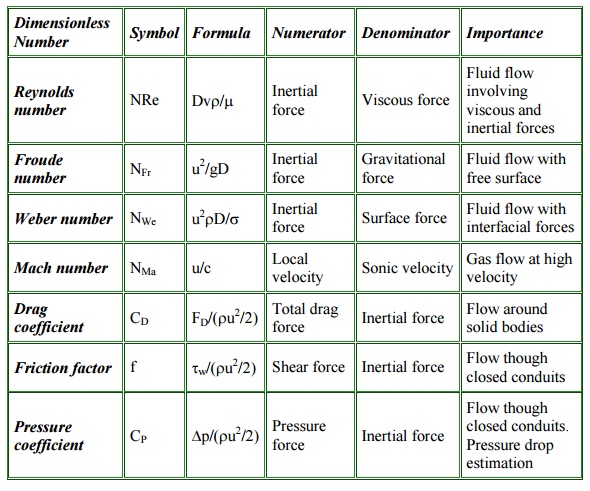
DIMENSIONLESS PARAMETERS

Since the inertia force is always present in a fluid flow, its ratio with each of the other forces provides a dimensionless number.

1. Reynold’s number

2. Froud’s number

3.   Euler’s number

4. Weber’s number

5. Mach’s number

Applications of dimensionless parameters

1. Reynold’s model law

2. Froud’s model law

3. Euler’s model law

4. Weber’s model law

5. Mach’s model law

Important Dimensionless Numbers in Fluid Mechanics:

MODEL ANALYSIS.

PRE REQUEST DISCUSSION

Present engineering practice makes use of model tests more frequently than most people realize. For example, whenever a new airplane is designed, tests are made not only on the general scale model but also on various components of the plane. Numerous tests are made on individual wing sections as well as on the engine pods and tail sections

Models of automobiles and high-speed trains are also tested in wind tunnels to predict the drag and flow patterns for the prototype. Information derived from these model studies often indicates potential problems that can be corrected before prototype is built, thereby saving considerable time and expense in development of the prototype.

Concepts

Much time, mony and energy goes into the design construction and eradication of hydraulic structures and machines.

To minimize the chances of failure, it is always desired that the tests to be performed on small size models of the structures or machines. The model is the small scale replica of the actual structure or machine. The actual structure or machine is Called prototype.

Applictions

1.     Civil engineering structures such as dams, canals etc.

2.     Design of harbor, ships and submarines

3.     Aero planes, rockets and machines.

4.     Marine engineers make extensive tests on model shop hulls to predict the drag of the ships

GLOSSARY

The three friction factor problems:

The friction factor relates six parameters of the flow:

1.     Pipe diameter

2.     Average velocity

3.     Fluid density

4.     Fluid viscosity

5.     Pipe roughness

6.     The frictional losses per unit mass.

Therefore, given any five of these, we can use the friction-factor charts to find the sixth.

Most often, instead of being interested in the average velocity, we are interested in the volumetric flow rate Q = (p/4)D²V

The three most common types of problems are the following:

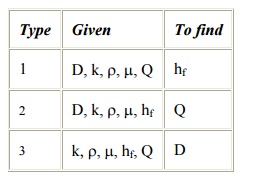
Generally, type 1 can be solved directly, where as types 2 and 3 require simple trial and error.

Three fundamental problems which are commonly encountered in pipe-flow calculations: Constants: rho, mu, g, L

1.     Given D, and v or Q, compute the pressure drop. (pressure-drop problem)

2.     Given D, delP, compute velocity or flow rate (flow-rate problem)

3.     Given Q, delP, compute the diameter D of the pipe (sizing problem)