Design Problem, Important Question And Answer: Civil - Limit State Design For Bond, Anchorage Shear and Torsion

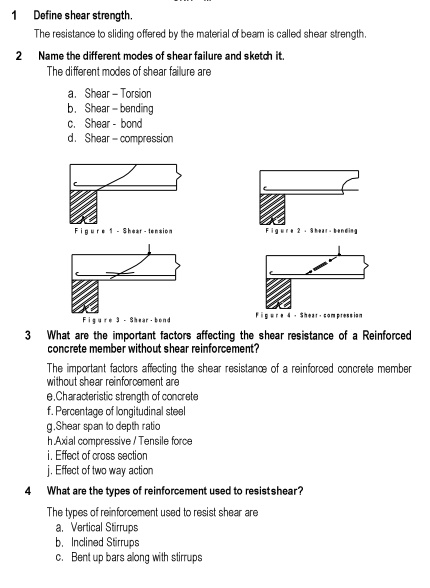
Problem :

Determine the anchorage length of 4-20T reinforcing bars going into the support of the simply supported beam shown in Fig. 6.15.5. The factored shear force V_u = 280 kN, width of the column support = 300 mm. Use M 20 concrete and Fe 415 steel.

DESIGN FOR TORSION

INTRODUCTION

Torsion when encountered in reinforced concrete members usually occurs in combination with flexure shear. Torsion in its associated„pure?with metalformshafts) is(generallyrarelyencounteredinreinforced concrete.

The interactive behavior of torsion with bending moment and flexural shear in reinforced concrete beams is fairly complex, owing to the no homogeneous, nonlinear and composite nature of the material and the presence of cracks. For convenience in design, codes prescribe highly simplified design procedures, which reflect a judicious blend of theoretical considerations and experimental results.

These design procedures and their bases are described in this chapter, following a brief review of the general behavior of reinforced concrete beams under torsion.

EQUILIBRIUM TORSION AND COMPATIBILITY TORSION

Torsion may be induced in a reinforced concrete member in various ways during the process of load transfer in

a structural system. In reinforced concrete desi commonly used to refer to two different torsion -inducing situations.

In      „equilibrium   torsion?,ducedbyaneccentric loading,theandtorsionequilibriumconditionsisaloneinsuffice

in determining the twisting moments. In „compati angle of twist and the resulting twisting moment depends on the torsional stiffness of the member.

In some (relatively rare) situations, axial force (tension or compression) may also be involved.

It must be clearly understood that this is merely a matter of terminology, and that it does not imply for instance, equilibrium conditions need not be satisfied in cases of

There are some situations (such as circular beams supported on multiple columns) where both equilibrium torsion and compatibility torsion coexist.

EQUILIBRIUM TORSION

This is associated with twisting moments that are developed in a structural member is maintain static equilibrium with the external loads, and are independent of the torsional stiffness of the member. Such torsion must be necessarily considered design. The magnitude of the twisting moment does not depend on the torsional stiffness of the member, and is entirely determinable from statics alone. The member has to be designed for the full torsion, which is transmitted by the member to the supports. More ever, the end(s) of the member should be suitably restrained to enable the member to resist effectively the torsion induced. Typically, equilibrium torsion is induced in beams supporting lateral over hanging projections, and is caused by the eccentricity in the loading (Figure). Such torsion is also induced in beams curved plan and subjected to gravity loads, and in beams where the transverse loads are eccentric with respect to the shear centre of the cross -section.

Compatibility Torsion  

This is the name given to the type of torsion induced in a member rotations (twists) applied at one or more points along the length of the member. It twisting moments induced are directly dependent on the torsional stiffness of the member. These moments are generally statically in determine and their analysis necessarily involves (rotational) compatibility in the floor beam system has shown in figure,Bat th the end B. As the primary (Spandrel) beam ABC is monolithically connected with the secondary beam BD at the joint B., compatibilityB inatthespandrelBimpliesbeamABC,and a bendinganangl moment will develop at the end b of beam BD. The bending moment will be equal to, and will act in a direction opposite to the twisting moment, in order_Bandthetwistingto/ sat bending moment at b depends on the torsional stiffness of beam ABC and the flexural stiffness of beam BD.

The torsional stiffness of a reinforced concrete member is drastically reduced by torsional cracking. This results in a very large increase in the angle of twist, induced twisting moment. For this reasons, the code (CL.40.1) permits the designer to neglect the torsional

stiffness of reinforced concrete members at the structural analysis stage itself, so that the need for detailed design for torsion in such cases does not arise at the design stage. With reference to figure, this implies assuming a fictitious hinge (i.e., no rotational restraint) at the end B of the beam BD, and assuming a continuous support (spring, support, actually)at the joint D. Incidentally, this assumption helps in reducing the degree of static indeterminacy of the structure (typically, a grid floor), thereby simplifying the problem of structural analysis. Thus, the code states:

In general, where the torsional resistance or stiffness of members has not been taken into account in the analysis of a structure no specific calculations for torsion will be necessary [CL40.1 of the code].

Of course, this simplification implies the acceptance of cracking and increased deformations in the torsional member. It also means that during the first time loading, a twisting moment up to the cracking torque of the the member, prior to torsional cracking. In order to control the subsequent cracking and to impart ductility to the member, it is desirable to provide a minimum torsional reinforcement,

equal to that required to resist the „cracking t reinforcement specified by the code (CL. 25.5.1.6) is to ensure some degree of control of torsional cracking of

beams due to compatibility torsion.

If, however, the designer chooses to consider „ that a realistic estimate of torsional stiffness is made for the purpose of structural analysis, and the required

torsional reinforcement should be provided for the calculated twisting moment.