Chapter: Civil : Mechanics Of Solids : Deflection Of Beams
Deflection Of Beams: Moment area method
Moment area
method
Theorems of
Area-Moment M ethod
Theorem I
The
change in slope between th e tangents drawn to the elastic curve at any t wo
points A and B is equal to the product of 1/EI m ultiplied by the area of the
moment diagra m between these two points.
Theorem II
The deviation of any point B r elative to the
tangent drawn to the elastic cu rve at any other point A, in a direction
perpendicular to the original position of the beam, is equal to the product of
1/EI multiplied by the moment of a n area about B of that part of the moment
dia gram between points A and B.
Rules of Sign
1.
The deviation at
any point is positive if the point lies above the tangent, negative if the
point is below the tangent.
2.
Measured from
left tangent, if ? is counterclockwise, the change of slope is positive,
negative if ? is clockwise.
Columns -
End conditions
Columns -end conditions
What is a Column or Strut?
Any machine member, subjected to the axial
compressive loading is called a strut and the vertical strut is called column
The columns are generally
categorized in two types: short columns and long columns. The one
with length less than eight times the diameter (or approximate diameter) is
called short column and the one with length more than thirty times the diameter
(or approximate diameter) is called long column.
Ideally, the columns should
fail by crushing or compressive stress and it normally happens for the short
columns, however, the long columns, most of the times, failure occurs by
buckling.
Euler's Buckling Formula
To get the correct results,
this formula should only be applied for the long columns. The buckling load
calculated by the Euler formula is given by:
Fbe =
(C*?2*E*I)/
Equivalent length of a column
Strength Of Columns
A stick of timber, a bar of
iron, etc., when used to sustain end loads which act lengthwise of the pieces,
are called columns, posts, or struts if they are so long that they would bend
before breaking. When they are so short that they would not bend before
breaking, they are called short blocks, and their compressive strengths are
computed by means of equation 1. The strengths of columns cannot, however, be
so simply determined, and we now proceed to explain the method of computing
them.
-> . End Conditions. The
strength of a column depends in part on the way in which its ends bear, or are
joined to other parts of a structure, that is, on its " end
conditions." There are practically but three kinds of end conditions,
namely:
1. "Hinge" or "pin" ends,
2. " Flat" or " square "
ends, and
3. "Fixed" ends.
(1) When a column is fastened to its support at
one end by means of a pin about which the column could rotate if the other end
were free, it is said to be "hinged" or "pinned" at the
former end. Bridge posts or columns are often hinged at the ends.
(2) A column either end of which is flat and
perpendicular to its axis and bears on other parts of the structure at that
surface, is said to be "flat" or " square" at that end.
(3) Columns are sometimes riveted near their ends
directly to other parts of the structure and do not bear directly on their
ends; such are called " fixed ended." A column which bears on its
flat ends is often fastened near the ends to other parts of the structure, and
such an end is also said to be " fixed." The fixing of an end of a
column stiffens and therefore strengthens it more or less, but the strength of
a column with fixed ends is computed as though its ends were flat. Accordingly
we have, so far as strength is concerned, the following classes of columns:
-> . Classes of Columns. (1)
Both ends hinged or pinned; (2) one end hinged and one flat; (3) both ends
flat.
Other things being the same, columns of these
three classes are unequal in strength. Columns of the first class are the
weakest, and those of the third class are the strongest.
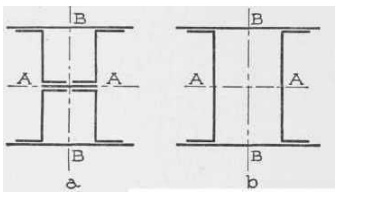
Fig. 46.
-> .
Cross=sections of Columns. Wooden columns are usually solid, square,
rectangular, or round in section; but sometimes they are "built up"
hollow. Cast-iron columns are practically always made hollow, and rectangular
or round in section. Steel columns are made of single rolled shapes - angles,
zees, channels, etc.; but the larger ones are usually "built up" of
several shapes. Fig. 46, a, for example, represents a cross-section of a
"Z-bar" column; and Fig. 46, b, that of a "channel" column.
-> .
Radius of Gyration. There is a quantity appearing in almost all formulas for
the strength of columns, which is called "radius of gyration." It
depends on the form and extent of the cross-section of the column, and may be
defined as follows:
The
radius of gyration of any plane figure (as the section of a column) with
respect to any line, is such a length that the square of this length multiplied
by the area of the figure equals the moment of inertia of the figure with
respect to the given line.
Thus, if A denotes the area of a figure; I,
its moment of inertia with respect to some line; and r, the radius: of gyration
with respect to that line; then

(9)
In
the column formulas, the radius of gyration always refers to an axis through
the center of gravity of the cross-section, and usually to that axis with
respect to which the radius of gyration (and moment of inertia) is least. (For
an exception, see example 3. Art. 83.) Hence the radius of gyration in this
connection is often called for brevity the "least radius of
gyration," or simply the "least radius."
Examples. 1. Show that the value of the
radius of gyration given for the square in Table A, page
The moment of inertia of the square with
respect to the axis is 1/12 a4- Since A = a2, then, by formula 9 above,
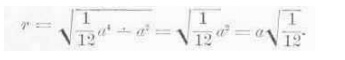
2. Prove that the value of
the radius of gyration given for the hollow square in Table A, page 54, is
correct.
The value of the moment of inertia of the
square with respect to the axis is 1/12 (a4 - a1 4). Since A = a2 - a12,
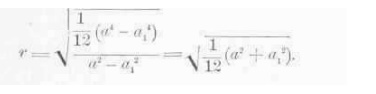
Related Topics