Deflection Of Beams: Euler equation

Euler equation

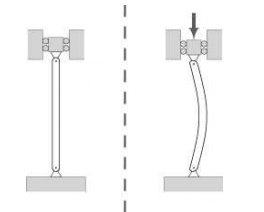
A column under a concentric axial load exhibiting the characteristic deformation of buckling

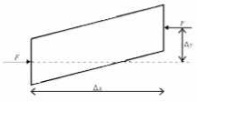
The eccentricity of the axial forrce results in a bending moment acting on the beam element.

The ratio of the effective length of a column to the least radius of gyration of its cross section is called the slenderness ratio (s ometimes expressed with the Greek letter l ambda, ?). This ratio affords a means of classifying columns. Slenderness ratio is important for d esign considerations. All the following are approximate values used for convenience.

·        A short steel column is one whose slenderness ratio does not exceed 50; an intermediate length steel column h as a slenderness ratio ranging from about 50 to 200, and are dominated by the stre ngth limit of the material, while a long steel column may be assumed to have a slend erness ratio greater than 200.

·        A short concrete colum n is one having a ratio of unsupported length to least dimension of the cross section not gr eater than 10. If the ratio is greater than 10 , it is a long column (sometimes referred to as a slender column).

·        Timber columns may b e classified as short columns if the ratio o f the length to least

dimension of the cross section is equal to or less than 10. The d ividing line between intermediate and long timber columns cannot be readily evaluated. One way of defining the lower limit of long t imber columns would be to set it as the smal lest value of the ratio of length to least cross sectional area that would just exceed a certain constant K of the material. Since K depends on the modulus of elasticity and the allowable compressive stress parallel to the grain, it can be seen that this arbitrary limit would vary with the species of the timber. The value of K is given in most structural handbooks.

If the load on a column is app lied through the center of gravity of its cros s section, it is called an axial load. A load at any other point in the cross section is known as an eccentric load. A short column under the action of an axial load will fail by direct compression be fore it buckles, but a long column loaded in the sam e manner will fail by buckling (bending), the buckling effect being so large that the effect of the direct load may be neglected. The intermedia te-length column will fail by a combination of direct compressive stress and bending.

In 1757, mathematician Leonhard Euler derived a formula that gives the maximum axial load that a long, slender, ideal col umn can carry without buckling. An ideal c olumn is one that is perfectly straight, homogeneo us, and free from initial stress. The maxim um load, sometimes called the critical load, causes the column to be in a state of unstable eq uilibrium; that is, the introduction of the slightest lateral force will cause the column to fail by buckling. The formula derived by Euler for columns w ith no consideration for lateral forces is given below. However, if lateral forces are taken into co nsideration the value of critical load remains approximately the same.

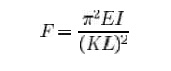
where

F = maximum or critica l force (vertical load on column), E = modulus of elasticit y,

I = area moment of inertia,

L = unsupported length of column,

K = column effective length factor, whose value depends on the con ditions of end support of the column, as follow s.

For both ends pinned (h inged, free to rotate), K = 1.0. For both ends fixed, K = 0.50.

For one end fixed and t he other end pinned, K = 0.699....

For one end fixed and t he other end free to move laterally, K = 2.0. KL is the effective lengtth of the column.

Examination of this formula reveals the following interesting facts with regard to the load-bearing ability of slender colum ns.

1.     Elasticity and not compressive strength of the materials of the column determines the critical load.

2.     The critical load is directly proportional to the second moment of area of the cross section.

3.     The  boundary  conditio ns  have  a  considerable  effect  on  the  crit ical  load  of  slender columns. The boundary conditions determine the mode of bend ing and the distance between inflection poi nts on the deflected column. The closer to gether the inflection points are, the higher the resulting capacity of the column.

A demonstration model illustra ting the different "Euler" buckling modes. The model shows how the boundary conditions affect the critical load of a slender column. Notice that each of the columns are identical, apart from the boundary conditions.

The strength of a column may t herefore be increased by distributing the material so as to increase the moment of inertia. This can be done without increasing the weigh t of the column by distributing the material as fa r from the principal axis of the cross secti on as possible, while keeping the material thick eno ugh to prevent local buckling. This bears ou t the well-known fact that a tubular section is much m ore efficient than a solid section for column service.

Another bit of information th at may be gleaned from this equation is the effect of length on critical load. For a given size column, doubling the unsupported length quarters the allowable load. The restraint offered by t he end connections of a column also affects the critical load. If the connections are perfectly rigidd, the critical load will be four times that for a similar column where there is no resistance to rotation (hinged at the ends).

Since the moment of inertia of a surface is its area multiplied by the square of a length called the radius of gyration, the above fo rmula may be rearranged as follows. Using the Euler formula for hinged ends, and substituting A ·r² for I, the following formula results.

where F / A is the allowable stress of the column, and l / r is the slenderness ratio.

Since structural columns are c ommonly of intermediate length, and it is im possible to obtain an ideal column, the Euler formula on its own has little practical application for ordinary design. Issues that cause deviation f rom the pure Euler strut behaviour inclu de imperfections in geometry in combination with plasticity/non-linear stress strain behaviour of the column's material. Consequently, a number of empirical column formulae have been developed to agree with test data, all of which embody the slenderness ratio. For design, appropriate safety factors are introduced into these formulae. One such formular is the Perry Robertson formula which estimates of the critical buckling load based on an initial ( small) curvature. The Rankine Gordon fomular is als o based on eperimental results and surgests t hat a strut will buckle at a load Fmax given by:

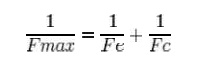
where Fe is the euler maximum load and Fc is the maximum compresivee load. This formular typically produces a conservative estimate of Fmax.

Self-buckling

A free-standing, vertical colummn, with density ?, Young's modulus E, and radius r, will buckle under its own weight if its height exceeds a certain critical height:

where g is the acceleration due to gravity, I is the second moment of ar ea of the beam cross section, and B is the first zero o f the Bessel function of the first kind of orde r -1/3, which is equal to 1.86635...

Slenderness ratio

Euler's Theory : The struts w hich fail by buckling can be analyzed by Euler's theory. In the following sections, different ca ses of the struts have been analyzed.

Case A: Strut with pinned en ds:

Consider an axially loaded stru t, shown below, and is subjected to an axial load „P' this load „P' produces a deflection „y' at a distance „x' from one end. Assume that the ends are either pin

jointed or rounded so that there is no moment at either end.

Assumption:

The strut is assumed to be initially straight, the end load being applied axially through centroid.

In this equation „M' is not a fu nction „x'. Therefore this equation can not be integrated directly as has been done in the case of de flection of beams by integration method.

Though this equation is in „y ' but we can't say at this stage where the deflection would be maximum or minimum.

So the above differential equation can be arranged in the following form

Let us define a operator

D = d/dx

(D2 + n2) y =0 where n2 = P/EI

This is a second order differ ential equation which has a solution of the form consisting of complimentary function and particular integral but for the time being we are interested in the complementary solution only[i n this P.I = 0; since the R.H.S of Diff. equatio n = 0]

Thus y = A cos (nx) + B sin (nxx)

Where A and B are some constants.

Therefore

In order to evaluate the constants A and B let us apply the boundary conditions,

(i) at x = 0; y = 0

(ii) at x = L ; y = 0

Applying the first boundary condition yields A = 0.

Applying the second boundary condition gives

From the above relationship the least value of P which will cause the strut to buckle, and it is called the " Euler Crippling Load " Pe from which w obtain.

The interpretation of the above analysis is that for all the values of the load P, other than those which make sin nL = 0; the strut will remain perfectly straight since

y = B sin nL = 0

For the particular value of

Then we say that the strut is in a state of neutral equilibrium, and theoretically any deflection which it suffers will be maintained. This is subjected to the limitation that „L' remains sensibly

constant and in practice slight increase in load at the critical value will cause the deflection to increase appreciably until the material fails by yielding.

Further it should be noted that the deflection is not proportional to load, and this applies to all strut problems; like wise it will be found that the maximum stress is not proportional to load.

The solution chosen of nL = p is just one particular solution; the solutions nL= 2p, 3p, 5p etc are equally valid mathematically and they do, infact, produce values of „Pe' which are equally valid

for modes of buckling of strut different from that of a simple bow. Theoretically therefore, there are an infinite number of values of Pe , each corresponding with a different mode of buckling.

The value selected above is so called the fundamental mode value and is the lowest critical load producing the single bow buckling condition.

The solution nL = 2p produces buckling in two half - waves, 3p in three half-waves etc.

If load is applied sufficiently quickly to the strut, then it is possible to pass through the fundamental mode and to achieve at least one of the other modes which are theoretically possible. In practical loading situations, however, this is rarely achieved since the high stress associated with the first critical condition generally ensures immediate collapse.