Conversion of Algebraic Expressions into Tree Diagrams

Conversion of Algebraic Expressions into Tree Diagrams

There is more fun with trees. Observe the following trees

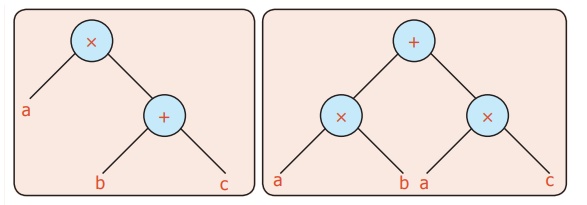
The above tree is nothing but the familiar equation a × (b + c) = (a × b) + (a × c). Thus we can see the algebraic expressions as trees.

• The tree on the left has less number of nodes and looks simple.

• The tree on the right has more number of nodes

• Can we conclude that the value of both the trees are different

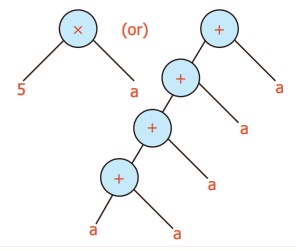
Example 15:

Convert ‘5a’ into Tree diagram

Solution:

Example 16:

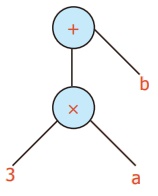
 Convert '3a + b' into Tree diagram

Algebraic expression

3a+b

Tree diagram

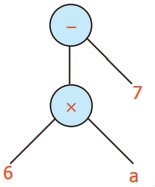
Example 17:

'6 times a and 7 less’ Convert into a Tree diagram.

Algebraic expression

 6a − 7

Tree diagram

Example 18:

Convert the tree diagram into an algebraic expression.

Tree diagram

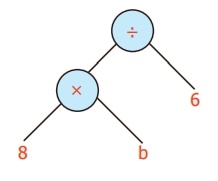
Algebraic expression

8b ÷ 6

Example 19:

Convert the tree diagram into an algebraic expression.

Tree diagram

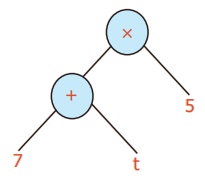
Algebraic expression

(7 + t) 5

Example 20:

Verify whether given trees are equal or not

Tree diagram

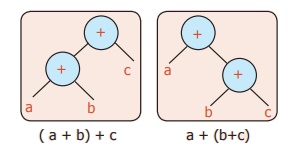
( a + b) + c = a + (b+c)

Yes, they are equal.

Try these

1. Check whether the Tree diagrams are equal or not

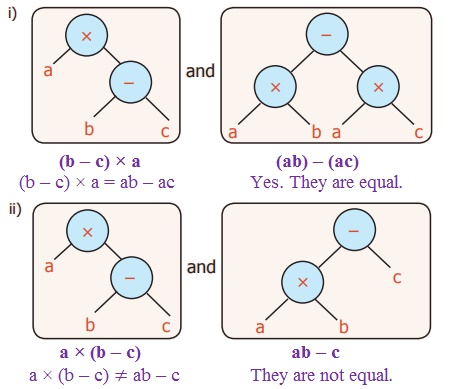
2. Check whether the following algebraic expressions are equal or not by using Tree diagrams

i) (x − y) + z and x − (y + z)

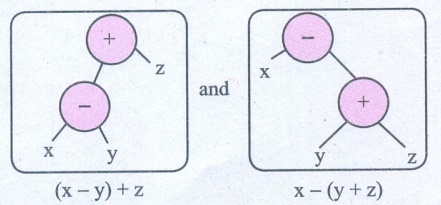
(x – y) + z  ≠ x – (y + z).

They are not equal.

ii) (p × q) × r and p × (q × r)

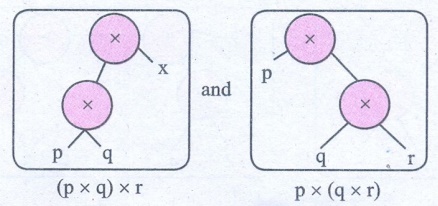
(p × q) × r = p × (q × r).

They are equal.

iii) a − (b − c) and (a − b) − c

a – (b – c) ≠ (a – b) – c

They are not equal.

Do You Know

Consider the numerical expression 9 – 4. which means 4 is to be subtracted from 9. 9 – 4 can be represented as – 9 4 (so far we have come across with operation in between the operands)

Suppose the expression is 9 – 4 × 2. This can be represented as × – 9 4 2 gives the meaning of

Step 1: × 9 – 4 2

Step 2: (9 – 4) × 2

Take the expression + × −  9 4 2 5

Step 1: + × 9 − 4 2 5

Step 2: + (9 − 4 ) × 2 5

Step 3: [(9 − 4) × 2] + 5

This is reading an expression from “left to right”. Similarly, we can read expressions from “right to left” also

9 4 2 5 + × −  can be read as “right to left” expression which gives the meaning of

9 4 2 5 + × => (9 − 4) 2 5 + ×

           => (9 − 4) × 2 5 +

           => [(9 − 4) × 2] + 5

Hence an expression can be read as “left to right” or “right to left” giving the same answer which is similar to name 4 as Naangu (நான்கு), Four, Nalagu (నాలుగు) and Char(चार), all of them representing the collection of four objects. Similarly the numerical expression

[ (9 – 4) × 8 ] ÷ [ (8 + 2) × 3] can be written as ÷ × – 9 4 8 × + 8 2 3 ( left to right) or 8 9 4 – × 3 8 2 + × ÷ ( right to left ).

Try these: 1) × – + 9 7 8 2

                  2) ÷ × + 2 3 8 5