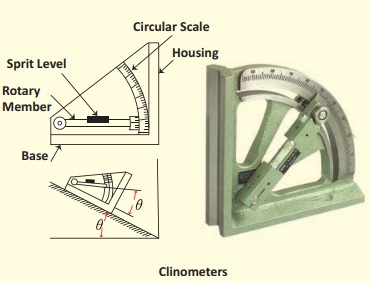
Clinometers

Clinometers

In this Instruction, we will learn how to use clinometers to measure the height of a tall object. What you will need; Clinometers, Tape, Paper, Pen or pencil, Assistant.

Step 1: Pick a Spot

Let us pick a spot to measure your object which may be a tree or electric or telephone pole. You should be far enough away from your object that you can see the top of it, and you need to be on level ground with the base of the object.

Step 2: Measure Angle

Here's where we bust out our handy clinometers. Look through the straw of your clinometers at the top of the tree or whatever object you're measuring. The weighted string should hang down freely, crossing the protractor portion of the clinometers. Read the angle shown, and subtract from 90° to find your angle of vision from your eye to the top of the tree (it can be helpful here to have an assistant to read the measurement while we look through the straw). We record our results on a paper. From the spot, the clinometers ( read by assistant) show 55°. Subtracting  from 90° that indicated that we looked at an angle of 35° to the top of the tree.

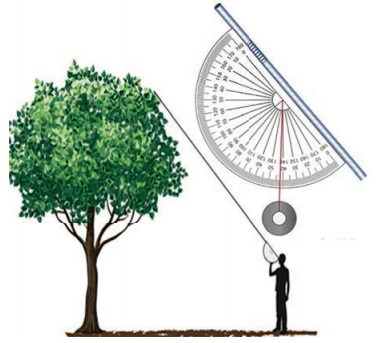
Step 3: Measure Distance

Once we have our angle of vision, we can use tape measure to find the distance from the spot we are standing to the base of the object we are measuring (an assistant comes in handy here, too). We must know how far away we are to accurately calculate the height. Our spot was 15.6 meters from the base of the tree we measured.

Step 4: Find Your Eye-height

The last piece of data you need to calculate the height of the object is the height from the ground to our eye (our eye-height). We must have the assistant help us measure this using our tape measure. Our eye height was recorded for this example as 1.64 metres.

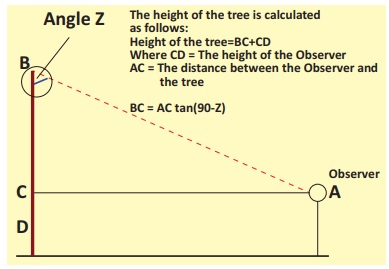
Step 5: Draw a Picture

In calculating the height of the object you just measured, we find it helpful to begin by drawing a picture and labeling it with all of the information we have.

Step 6: Model as a Triangle

The next step is to simplify our drawing to model our system as a right triangle. Label our triangle with the angle we read on our clinometers as well as the distance you were standing from the object (we don't need the eye-height just yet).

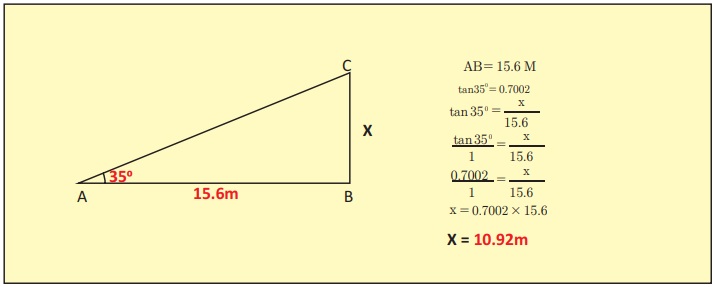
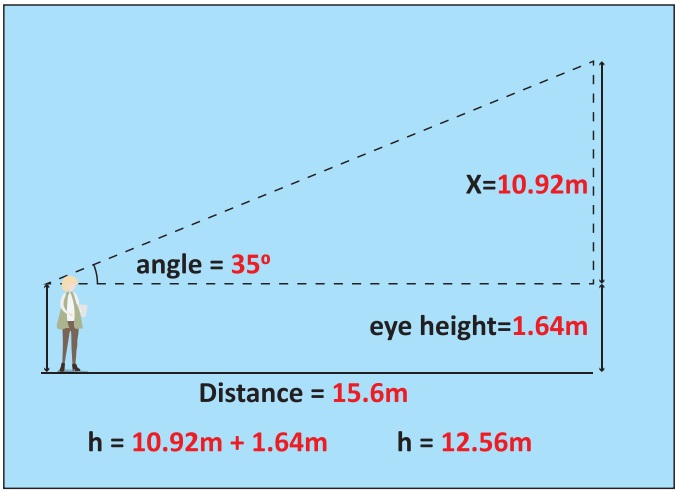
We can find x in this triangle (which represents the portion of the height from eye-level up) by using some basic trigonometry, specifically the tangent ratio of the triangle:

Tan (angle) = x / distance

Multiply by the distance on both sides and you get:

x = tan (angle) * distance

Use a calculator to multiply these together and get a decimal value.

In the example:

Tan (35°) = x / 15.6

x = tan(35°) * 15.6

x = 10.92 metres

Step 7: Combine with Eye Height

To find the height of our object, we bring this x value back to the original drawing. By labeling it, we can see that the height of the object, h, is equal to the x value we just found plus the eye-height we measured earlier:

h = x + (eye-height)

In the example:

h = 10.92m + 1.64m

h = 12.56m

Exercise

Find out the height of the building shown below. Or Find out the height of a tree or building or electric pole near your premise. Given eye sight and distance from the building are 1.5m and 18m respectively