Chapter: Transmission Lines and Waveguides : Waveguides and Cavity Resonators
Besselãs differential equation and Bessel function & TM and TE waves in Circular wave guides
Besselãs differential equation and Bessel function & TM and TE waves in Circular wave guides
A circular waveguide is a hollow metallic tube with circular cross section for propagating the electromagnetic waves by continuous reflections from the surfaces or walls of the guide.
The circular waveguides are avoided because of the following reasons:
a) The frequency difference between the lowest frequency on the dominant mode and the next mode is smaller than in a rectangular waveguide, with b/a= 0.5
b) The circular symmetry of the waveguide may reflect on the possibility of the wave not maintaining its polarization throughout the length of the guide.
c) For the same operating frequency, circular waveguide is bigger in size than a rectangular waveguide.


Note: h fulfills the pth root of Jn(ha)=0 for TMnp mode, and h fulfills the pth root of Jãn(ha)=0 for TEnp mode
Case 2
TEnp modes: Ez=0, ã§t2Hz+h2Hz=0 ã Hz0 (r,ü) = C'n Jn (hr)cosnü
Waveguideãs equations

Note: TE11 mode is the fundament (dominant) mode of a circular waveguide.
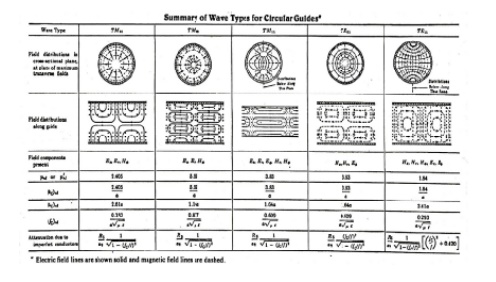
The possible TM modes in a circular waveguide are: TM01, TM02, TM11, TM12.
The root values for the TM modes are:
ã (ha)01 = 2.405 for TM01
ã (ha)02 = 5.53 for TM02
ã (ha)11 = 3.85 for TM11
ã (ha)12 = 7.02 for TM12
The dominant mode for a circular waveguide is defined as the lowest order mode having the lowest root value.
The possible TE modes in a circular waveguide are: TE01, TE02, TE11, TE12.
The root values for the TE modes are:
ã (ha)01 = 3.85 for TE01
ã (ha)02 = 7.02 for TE02
ã (ha)11 = 1.841 for TE11
ã (ha)12 = 5.53 for TE12
The dominant mode for TE waves in a circular waveguide is the TE11.v. Because it has the lowest root value of 1.841.
Since the root value of TE11 is lower than TM01, TE11 is the dominant or the lowest order mode for a circular waveguide.
Problem: A 10GHz signal is to be transmitted inside a hollow circular conducting pipe. Determine the inside diameter of the pipe such that its lowest cutoff frequency is 20% below this signal frequency. (b) If the pipe is to operate at 15GHz, what waveguide modes can propagate in the pipe?
(Sol.)

Applications of circular waveguide.
ã Circular waveguides are used as attenuators and phase-shifters
Related Topics