Area

Area:

The area is a measure of how much space there is on a flat surface.

The area of the plot of land is derived by multiplying the length and breadth

Area = length × breadth

The unit of the area is = metre × metre

                    =   metre²

                    =   m² ( Read as square metre)

Area is a derived quantity as we obtain are by multiplying twice of the fundamental physical quantity length.

One square metre is the area enclosed inside a square of side 1 metre.

Problem 1.1

What is the area of a 10 squares each of side of 1 m.

Area of a square = side × side

                               =1 m × 1 m

                               =1 m² or 1 square metre

Area of 10 squares = 1 square metre × 10

                               = 10 square metre

(Even though the area is given in square metre , the surface need not to be square in shape)

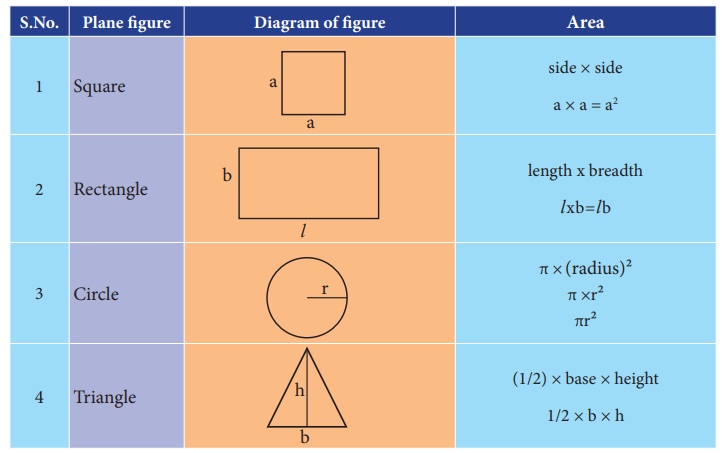
Area of regularly shaped figures

The area of regularly shaped figures can be calculated using the relevant formulae. In the table 1.2, the formulae used to calculate the area of certain regularly shaped figures are given.

Problem 1.2

Find the area of the following regular shaped figures: (Take π = 22/7)

a. A rectangle whose length is 12 m and breadth is 4 m.

b. A circle whose radius is 7 m.

c. A triangle whose base is 6 m and height is 8 m.

Solution:

(a) Area of rectangle = length × breadth

                                = 12×4

                                = 48 m²

(b) Area of circle= π × r² = (22/7) × 7 × 7

                                        = 154 m²

(c) Area of triangle = (1/2) × base × height

                             = (1/2)   × 6 × 8

                             = 24 m²

Table 1.2 Area of some regularly shaped figures

Area of irregularly shaped figures

In our daily life, we encounter many irregularly shaped figures like leaves, maps, stickers of stars or flowers, peacock feather etc. The area of such irregularly shaped figures cannot be calculated using any formula.

How can we find the area of these irregularly shaped objects?

We can find the area of these figures with the help of a graph sheet.

The following activity shows how to find the area of irregularly shaped plane figures.

The graphical method explained above can be used to find the area of regularly shaped figures also. In the case of square and rectangle, this method gives the area accurately.

ACTIVITY 1

Take a leaf from any one of trees in your neighbourhood. Place the leaf on a graph sheet and draw the outline of the leaf with a pencil (Figure 1.2). Remove the leaf. You can see the outline of the leaf on the graph sheet.

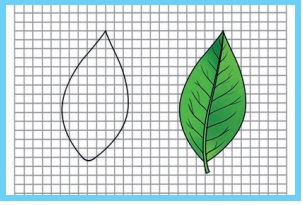
Figure 1.1  Area of an irregularly shaped plane figure

i. Now, count the number of whole squares enclosed within the outline of the leaf. Take it to be M.

ii. Then, count the number of squares that are more than half. Take it as N.

iii. Next, count the number of squares which are half of a whole square. Note it to be 

P. Finally, count the number of squares that are less than half. Let it be Q.

v. M =  51 ; N =  15 ; P = 4; Q =  11

Now, the approximate area of the leaf can be calculated using the following formula:

Approximate area of the leaf = M + (3/4) N + (1/2) P + (1/4) Q square cm. 

Area of the leaf = 51+ (¾) × 15 + (½) × 4 + (¼) × 11.

= 51 + 11.25 + 2 + 2.75 = 67 square cm. 

This formula can be used to calculate the area of any irregularly shaped plane figures.