Archs - Structural Analysis

ARCHS

ARCH

An arch is defined as a curved girder, having convexity upwards and supported at its ends.

The supports must effectively arrest displacements in the vertical and horizontal directions. Only then there will be arch action.

2.Linear arch

If an arch is to take loads, say W₁, W₂, and W₃ and a vector diagram and funicular polygon are plotted as shown; the funicular polygon is known as the linear arch or theoretical arch.

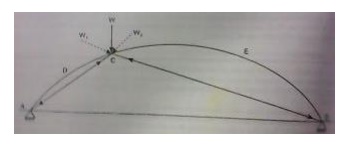
The polar distance 'ot'represents the horizontal thrust.

The links AC, CD, DE and EB will br under compression and there will be no bending moment. If an arch of this shape ACDEB is provided, there will be no bending moment.

3.Eddy'stheorem.

Eddy'stheorem states that 'The bending moment at any section of an arch is proportional to the vertical intercept between the linear arch (or theoretical arch) and the center line of the actual arch'.

BM_x = ordinate O₂ O₃ * scale factor

Degree of static indeterminacy of a three hinged parabolic arch

For a three-hinged parabolic arch, the degree of static indeterminacy is zero. It is statically determinate.

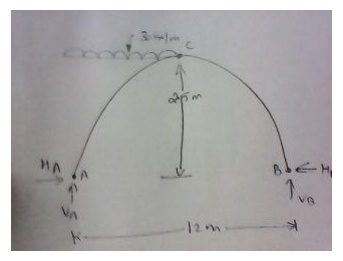
1.A three hinged parabolic arch hinged at the crown and springing has a horizontal span of 12m and a central rise of 2.5m. it carries a udl of 30 kN/m run over the left hand half of the span. Calculate the resultant at the end hinges.

Let us take a section X of an arch. Let ?be the inclination of the tangent at X. if H is the horizontal thrust and V the net vertical shear at X, from theb free body of the RHS of the arch, it is clear that V and H will have normal and radial components given by,

N = H cos ?+ V sin ? R = V cos?-H sin ?

The normal thrust and radial shear in an arch rib.

Parabolic arches are preferable to carry distributed loads. Because, both, the shape of the arch and the shape of the bending moment diagram are parabolic. Hence the intercept between the theoretical arch and actual arch is zero everywhere. Hence, the bending moment at every section of the arch will be zero. The arch will be under pure compression that will be economical.

Difference  between  the  basic  action  of  an  arch  and  a suspension cable

An arch is essentially a compression member, which can also take bending moments and shears. Bending moment and shears will be absent if the arch is parabolic and the loading uniformly distributed.

A cable can take only tension. A suspension bridge will therefore have a cable and a stiffening girder. The girder will take the bending moment and shears in the bridge and the cable, only tension.

Because of the thrust in cables and arches, the bending moments are considerably reduced.

If the load on the girder in uniform. The bridge will have only cable tension and no bending moment on the girder.

Under what conditions will the bending moment in an arch be zero throughout

The bending moment in an arch throughout the span will be zero, if

(i)                The arch is parabolic and

(ii)             The arch carries udl throughout the span

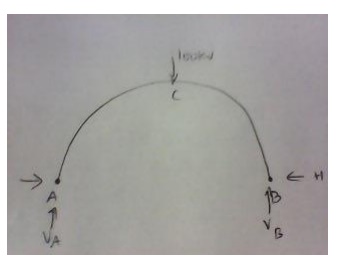
2.A three-hinged semicircular arch carries a point load of 100 kN at the crown. The radius of the arch is 4m. Find the horizontal reactions at the supports.

V_A = V_B = 50 kN

Equating the moment about C to Zero, V_A * 4 -H*4 = 0

H = V_A

Horizontal reaction, H = 50 kN

3.A three-hinged semicircular arch of radius 10m carries a udl of 2 kN/m over the span. Determine the horizontal and vertical reactions at the supports.

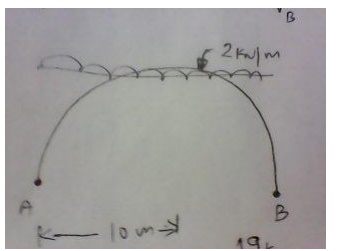
Determine H, V_A and V_B in the semicircular arch shown in fig

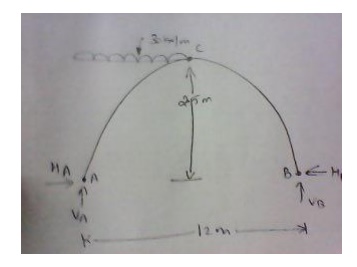
Equating moments about A to Zero,

V_B * 12 -12 * 9 = 0;

V_B = 9 kN                                and V_A = 3 kN

Equating moments to the left of C to zero,

H = V_A = 3 kN;                                 H= 3 kN

Distinguish between two hinged and three hinged arches.

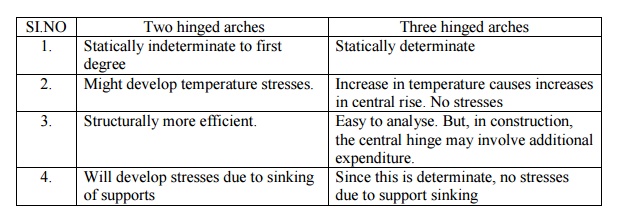
Two hinged arches

Statically indeterminate to first degree

Might develop temperature stresses.

Structurally more efficient.

Will develop stresses due to sinking of supports

Three hinged arches

Statically determinate

Increase in temperature causes increases in central rise. No stresses

Easy to analyse. But, in construction, the central hinge may involve additional expenditure.

Since this is determinate, no stresses due to support sinking

Rib -shorting in the case of arches.

In a 2-hinged arch, the normal thrust, which is a compressive force along the axis of the arch, will shorten then rib of the arch. This is turn will release part of the horizontal thrust.

Normally, this effect is not considered in the analysis (in the case of two hinged arches). Depending upon the important of the work we can either take into account or omit the effect of rib shortening. This will be done by considering (or omitting) strain energy due to axial compression along with the strain energy due to bending in evaluating H.

Effect of yielding of support in the case of an arch.

Yielding of supports has no effect in the case of a 3 hinged arch which is determinate. These displacements must be taken into account when we analyse 2 hinged or fixed arches as under

Here U is the strain energy of the arch ?H and ?V_A are the displacements due to yielding of supports.

5.A three-hinged parabolic arch has a horizontal span of 36m with a central rise of 6m. A point load of 40 kN moves across the span from the left to the right. What is the absolute maximum positive bending moment that wills occur in the arch

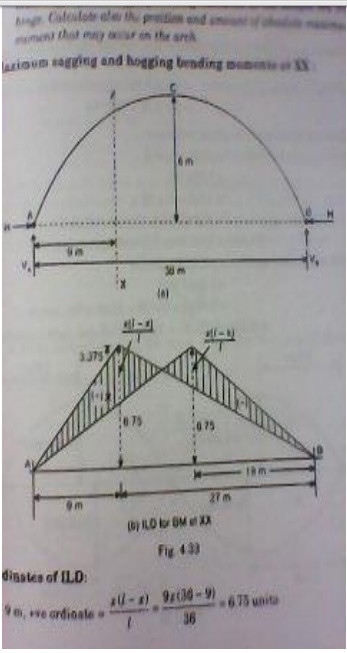
For a single concentrated load moving from one end to the other, Absolute maximum positive bending moment

= 0.096wl = 0.096*40 * 36=138.24 kNm This occurs at 0.211 l = 0.211 * 36 = 7.596 m from the ends.

Absolute maximum positive bending moment = 138.24 kNm at 7.596 m from the ends.

6.A 3 hinged arch of span 40m and rise 8m carries concentrated loads of 200 kN and 150 kN at a distance of 8m and 16m from the left end and an udl of 50 kN/m on the right half of the span. Find the horizontal thrust.

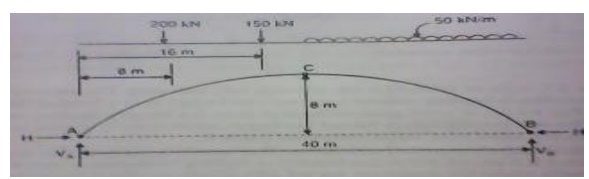
Solution:

(a) Vertical reactions V_A and V_B :

Taking moments about A,

200(8) + 150(16) + 50 * 20 * (20 + 20/2) -V_B (40) = 0

1600 + 2400 + 30000 -40 V_B = 0

V_B= = 850 kN

V_A = Total load -V_B = 200 + 150 + 50 * 20 -850 = 500 kN

(b) Horizontal thrust (H)

Taking moments about C,

-H x 8 + V_A (20) -200 (20 -8) -150 (20 -16) = 0 -8H + 500 * 20 -200 (12) -150 (4) = 0

H = 875 kN

7.A parabolic 3-hinged arch carries a udl of 30kN/m on the left half of the span. It has a span of 16m and central rise of 3m. Determine the resultant reaction at supports. Find the bending moment, normal thrust and radial shear at xx, and 2m from left support.

 Solution:

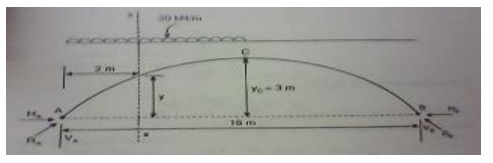
(1) Reaction at A nd B;

(i)                Vertical components of reactions;

Taking moments about A,

-V_B (16) + 30 x 8² /2 = 0

- V_B (16) + 30 * 32 = 0 V_B = 60 kN

V_A = Total load -V_B = 30 * 8 -60 kN V_A = 180 kN

(ii)                Horizontal components of reactions at A and

(2) Bending moment at x = 2m from A:

Bending moment = V_A (2) -30 * 2 *1 -H_A(y)  ---- (1)

Substitute in (1)y = 1.3125 m at x = 2m fromA''.

Bending moment at x                            = 2m from A = 180 (2) -30 * 2 * 1 -160 * 1.3125

Bending moment at xx                          = 90 kNm

(3) Radial shear force at x = 2m from A

Shear force, R_X = V_x cos ?-H sin ? Where, V = Net vertical shear force at x = 2m from A

= V_A - w (2) = 180 -30 * 2 V = 120 kN

H = Horizontal shear force = 160 kN

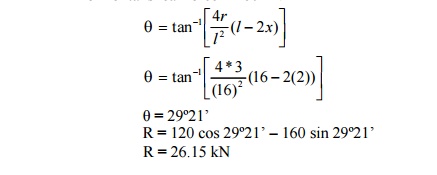
(4) Normal thrust at x = 2m from A:

Normal thrust P_N = V_x sin?+ H cos ?= 120 sin 29º21'+160cos 29º21' P_N = 198.28 kN.

8.A parabolic 3-hinged arch carries loads as shown in fig. Determine the resultant reactions at supports. Find the bending moment, normal thrust and radial shear at D, 5m from A. What is the maximum bending moment

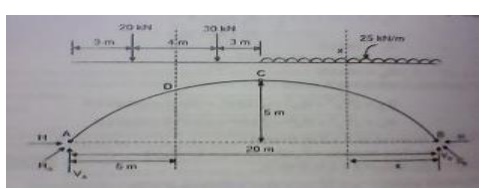
Solution:

(1)Reaction at supports: (R_A and R_B)

(i) Vertical components of R_A and R_B : (V_A and V_B) Taking moments about A,

20 * 3 + 30 (7) + 25 * 10 * (10 +10/2) -V_B *(20) = 0 V_B = 201 kN

V_A = Total load -V_B = 20 + 30 + 25 * 10 -201 V_A = 99 kN

(ii) Horizontal thrust (H):

Taking moments about the crown point C, considering the right

side of 'C',

-V_B (20/2) + H (5) + 25 * 10 *5 = 0 -201 * (20/2) + 5 H + 1250 + 0

H = 125 kN (iii) Resultant reactions R_A and R_B ;

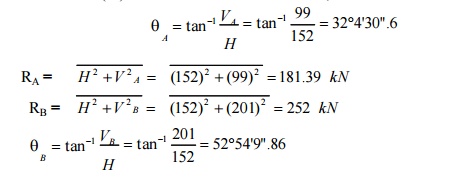
2. Bending moment, normal thrust and radial shear force (at D):

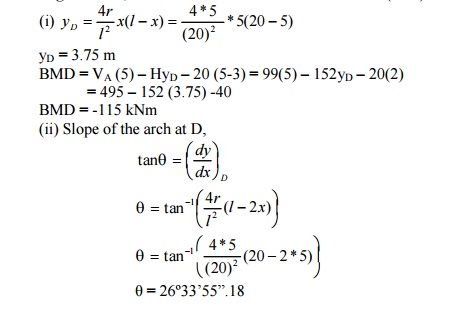
(iii) Normal thrust

P = V sin ?+ H cos ?

V = Net beam shear force = V_A -20 V = 99 -20 = 79 kN

Substitute in (iii) P = 79 sin ?+ 152 cos ?= 179.28 kN (iv) Radial shear force

F = V cos ?-H sin ?

F = 79 cos ?-152 sin ?= 2.683 kN

3. Maximum Bending Moment in CB:

Considering a section xx at a distance of 'x' fromm B'' BM_xx = 254KNM

9.A 3-hinged arch is circular, 25 m in span with a central rise of 5m. It is loaded with a concentrated load of 10 kN at 7.5m from the left hand hinge. Find the

(a) Horizontal thrust

(b) Reaction at each end hinge

(c)  Bending moment under the load

Solution:

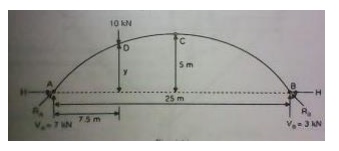
ertical reactions V_A and V_B:

Taking moments about A, 10(7.5) -V_B (25) = 0

V_B = 3 kN

V_A = Total load -V_B = 10 -3 = 7 kN

1.Horizontal thrust (H):

Taking moments about C

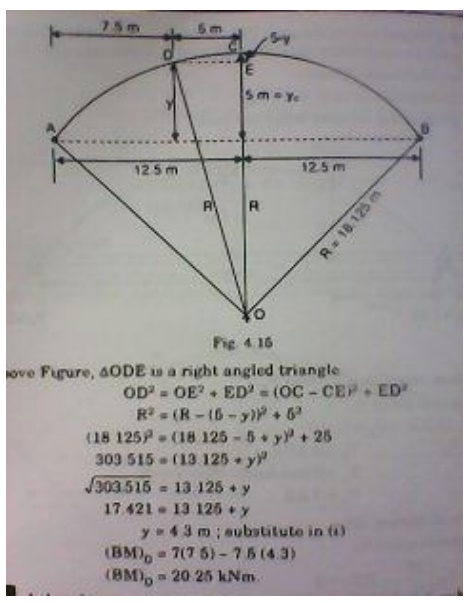
10.A three hinged circular arch of span 16m and rise 4m is subjected to two point loads of 100 kN and 80 kN at the left and right quarter span points respectively. Find the reactions at supports. Find also the bending moment, radial shear and normal thrust at 6m from left support.

Solution:

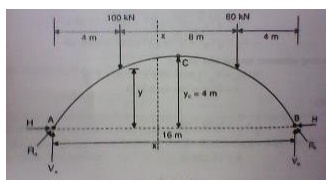
(a) Reaction at A and B:

(i)    Vertical components of reactions at A and B:

Taking moment about A,

100 (4) + 80(12) -V_B(16) = 0 V_B = 85 kN.

V_A = Total load - V_B = (100+80)-85 V_A = 95 kN.

b. Horizontal components of reactions at A and B; Taking moments about the crone points C

V_A(8) -H(Y_C) - 100(4) = 0 95 (8) -H (y_C ) -100 (4) = 0

H = 90 kN

(iii)Resultant reactions at A and B:

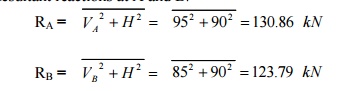
b) Bending moment at 6m from the left support:

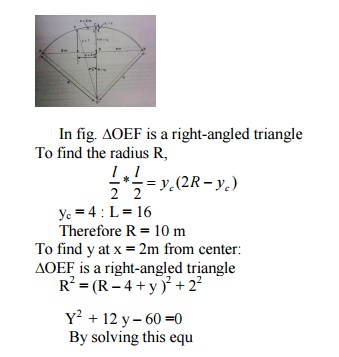
(c) Radial shear force 'F'   :

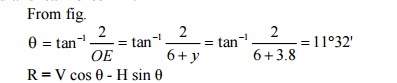
R = V cos ?- H sin ?

V = net shear force at x = 6m from A

= V_A -100 = 95 -100 = -5 kN H = 90 kN

R = -5 cos (11º32')-90 sin (11º32')= - 22.895 R = -22.89 kN

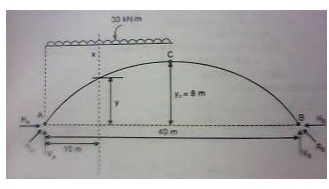
11.A symmetrical three hinged parabolic arch of span 40m and rise 8m carries an udl of 30 kN/m over left of the span. The hinges are provided at these supports and at the center of the arch. Calculate the reactions at the supports. Also calculate the bending moment, radial shear, normal thrust at distance of 10 m from the left support.

Solution:

(1) Reactions at the supports:

(i)Vertical components;

Taking moments about A,

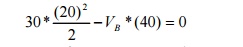
Vertical component of R_B,    V_B = 150 kN

V_A = Total load -V_B = 30 * 20 -150 = 450 kN

(iii)Horizontal components

Taking moments about the crown, 'C',

(22) Bending moment at 10 m from A:

(3)Radial shear force at x = 10m:

R = Radial shear force = V cos ?-H sin ? Where, V = Net vertical shear force at x = 10m from A

H = Horizontal thrust.

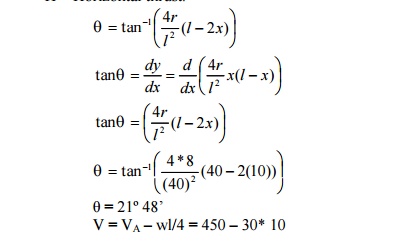
Radial shear force, R = V cos ?-H sin ?

R = 150 cos   21º-37548'sin   21º48'

R = 0

(4) Normal thrust at x = 10m from 'A':

Normal thrust, N = V sin ?+ H cos ?= 150 sin 21º48'375 cos+ 21?48' N = 403.89 kN

12.A parabolic 3-hinged arch of span 'l'issubjected to an u.d.l of w/m run over the entire span. Find the horizontal thrust and bending moment at any section XX.

Solution:

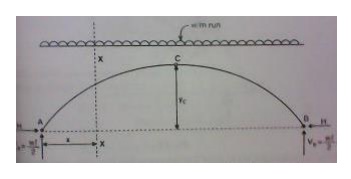
(a) Reactions (Vertical) at the supports:

As the loading is symmetrical, vertical reactions at A and B are equal V_A = V_B = Total load/2 = wl/2

(b) Horizontal thrust:

Taking moments about the crown point C,

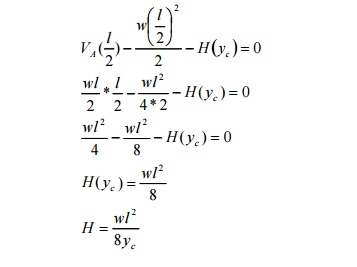
(c)  Bending moment at xx;