Working Stress Method Design

WORKING STRESS METHOD DESIGN

GENERAL PRINCIPLES OF WORKING STRESS DESIGN

(a) General features

During the early part of 20^th century, elastic theory of reinforced concrete sections outlined was developed which formed the basis of the working stress or permissible stress method of design of reinforced concrete members. In this method, the working or permissible stress in concrete and steel are obtained applying appropriate partial safety factors to the characteristics strength of the materials. The permissible stresses in concrete and steel are well within the linear elastic range of the materials.

The design based on the working stress method although ensures safety of the structures at working or services loads, it does not provide a realistic estimate of the ultimate or collapse load of the structure in contrast to the limit state method of design. The working stress method of design results in comparatively larger and conservative sections of the structural elements with higher quantities of steel reinforcement which results in conservative and costly design. Structural engineers have used this

method extensively during the 20^th century and presently the method is incorporated as an alternative to the limit state method in Annexure -B of the recently revised Indian Standard Code Is : 456 -2000 for specific applications.

The permissible stresses in concrete under service loads for the various stress states of compressive, flexure and bond is compiled in Table 2.1 (Table 21 of IS ; 456 -2000)

The permissible stress in different types of steel reinforcement is shown in table 2.2 (Table 22 of IS 456

-2000)

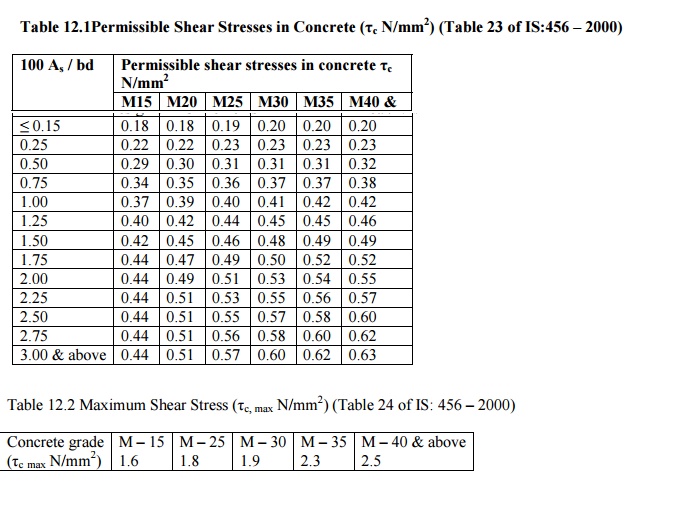
The permissible shear stress for various grades of concrete in beams is shown in Table 12.1 (Table 23 of IS: 456 -2000)

The maximum shear stress permissible in concrete for different grades is shown in Table 12.2 Table 12.2 (Table 24 of IS: 456 -2000)

In the case of reinforced concrete slabs, the permissible shear stress in concrete is obtained by multiplying the values given in Table 2.1 by as shown in Table 12.3 (Section 40.2.1.1. of IS; 456 -2000)

Note: A_s is that area of longitudinal tension reinforcement which continues at least one effective depth beyond the section being considered except at supports where the full area of tension reinforcement may be used provided the detailing conforms to 26.2.3.

The maximum shear stress permissible in concrete for different grades is shown in Table 12.2 (Table 24 of IS 456 -2000)

In the case of reinforced concrete slabs, the permissible shear stress in concrete is obtained by multiplying the3 values in Table 2.1 by a fac shown in Table 12.3 (Section 40.2.1.1. of IS 456 -2000)

(b) General design procedure

In the working stress design, the cross -sectional dimensions are assumed based on the basic span / depth ratios outlined in Chapter 5 (Table 5.1 and 5.2) (Section 23.2.1. of IS: 456 -2000)

The working load moments and shear forces are evaluated at critical sections and the required effective depth is checked by using the relation:

d    =   ?   M   /   Q.b

Where d = effective depth of section M = working load moment b = width of section

Q = a constant depending upon the working stresses in concrete and steel, neutral axis depth factor (k) and lever arm coefficient (f).

For different grades of concretepiledin Tableand2.3. steelThedepth th provided should be equal to or greater than the depth computed by the relation and the area of reinforcement required in the section to resi

The number of steel bars required is selected with due regard to the spacing of bars and cover requirements.

After complying with flexure, the section is generally checked for resistance against shear forces by calculating the_c givennominal=(Vby/bd)shear? stress ?

Where V = Working shear force at critical section.

The permissible shear_c)depends uponstressthepercentagereinforcementsconcreteinthecross -(? section and grade of concrete as shown in Table 12.1

If_c< ?_vsuitable? shear reinforcements are designed in beams at a spacing s_v given by the relation;

S_v = [ 0.87 f_y A_sv d / V_us]

Where s_v = spacing of stirrups

A_sv = cross -sectional area of stirrups legs

f_y = Characteristics strength of stirrup reinforcement

d = effective depth

V_s = [ V -?_c.b .d]

If_v< ?_c, nominal? shear reinforcements are provided in beams are provided in beams at a spacing given by

S_v [ 0.87 f_y  A_st / 0.4 b]

In case of slabs, the permissible shear stres Also in the case of slabs_v)shouldnot excetheed nominalhalfthe_cmaxsheshownvalueinrs

Table 12.2. In such cases the thickness of the slab is increased and the slab is redesigned.

In the case of compression members, the axial load permissible on a short column reinforced with longitudinal bars and lateral ties is given by

P    =_cc A(?_c+_sc ?A_sc)

Where s_cc = permissible stress in concrete in direct compression (Refer Table 2.1)

A_c = cross -sectional area of concrete excluding the area of reinforcements.

S_sc = permissible compressive stress in reinforcement

A_sc = cross -sectional area of longitudinal steel bars.