Limit State Of Collapse: Compression

LIMIT STATE OF COLLAPSE: COMPRESSION

Assumptions

1.    The maximum compressive strain in concrete in axial compression is taken as 0.002.

2.    The maximum compressive strain at the highly compressed extreme fibre in concrete subjected to axial compression and bending and when there is no tension on the section shall be 0.0035 minus 0.75 times the strain at the least compressed extreme fibre.

In addition the following assumptions of flexure are also required

3.    Plane sections normal to the axis remain plane after bending.

4.    The maximum strain in concrete at the outermost compression fibre is taken as 0.0035 in bending.

5.    The relationship between the compressive stress distribution in concrete and the strain in concrete may be assumed to be rectangle, trapezoid, parabola or any other shape which results in prediction of strength in substantial agreement with the results of test.

6.    An acceptable stress strain curve is given in IS:456-200. For design purposes, the compressive strength of concrete in the structure shall be assumed to be 0.67 times the characteristic strength. The partial safety factor y of 1.5 shall be applied in addition to this.

7.    The tensile strength of the concrete is ignored.

8.    The stresses in the reinforcement are derived from representative stress-strain curve for the type of steel used. Typical curves are given in IS:456-2000. For design purposes the partial safety factor equal to 1.15 shall be applied.

Minimum eccentricity

As per IS:456-2000, all columns shall be designed for minimum eccentricity, equal to the unsupported length of column/ 500 plus lateral dimensions/30, subject to a minimum of 20 mm. Where bi-axial bending is considered, it is sufficient to ensure that eccentricity exceeds the minimum about one axis at a time.

Short Axially Loaded Members in Compression

The member shall be designed by considering the assumptions given in 39.1 and the minimum eccentricity. When the minimum eccentricity as per 25.4 does not exceed 0.05 times the lateral dimension, the members may be designed by the following equation:

P_u = 0.4 f_ck A_c + 0.67 f_y A_sc

P_u = axial load on the member,

f_ck = characteristic compressive strength of the concrete, A_c = area of concrete,

f_{y =} characteristic strength of the compression reinforcement, and A_s = area of longitudinal reinforcement for columns.

Compression Members with Helical Reinforcement

The strength of compression members with helical reinforcement satisfying the requirement of IS: 456 shall be taken as 1.05 times the strength of similar member with lateral ties.

The ratio of the volume of helical reinforcement to the volume of the core shall not be less than

V_hs / V_c  >  0.36 (A_g/A_c - 1) f_ck/f_y

A_g = gross area of the section,

A_c = area of the core of the helically reinforced column measured to the outside diameter of the helix,

f_ck = characteristic compressive strength of the concrete, and

f_y =  characteristic strength of the helical reinforcement but not exceeding 415 N/mm.

Members Subjected to Combined Axial Load and Uni-axial Bending

Use of Non-dimensional Interaction Diagrams as Design Aids

Design Charts (for Uniaxial Eccentric Compression) in SP-16

The design Charts (non-dimensional interaction curves) given in the Design Handbook, SP : 16 cover the following three cases of symmetrically arranged reinforcement :

(a)Rectangular sections with reinforcement distributed equally on two sides (Charts 27 - 38): the 'two sides' refer to the sides parallel to the axis of bending; there are no inner rows of bars, and each outer row has an area of 0.5A_s this includes the simple 4-bar configuration.

(b) Rectangular sections with reinforcement distributed equally on four sides (Charts 39 - 50): two outer rows (with area 0.3A_s each) and four inner rows (with area 0.1A_s each) have been considered in the calculations ; however, the use of these Charts can be extended, without significant error, to cases of not less than two inner rows (with a

minimum area 0.3A in each outer row).

s

(c) Circular column sections (Charts 51 - 62): the Charts are applicable for circular sections with at least six bars (of equal diameter) uniformly spaced circumferentially.

Corresponding to each of the above three cases, there are as many as 12 Charts available covering the 3 grades of steel (Fe 250, Fe 415, Fe 500), with 4 values of d¹/ D ratio for each grade (namely 0.05, .0.10, 0.15, 0.20). For intermediate values of d¹/ D, linear interpolation may be done. Each of the 12 Charts of SP-16 covers a family of non-dimensional design interaction curves with p/f_ck values ranging from 0.0 to 0.26.

From this, percentage of steel (p) can be found. Find the area of steel and provide the required number of bars with proper arrangement of steel as shown in the chart.

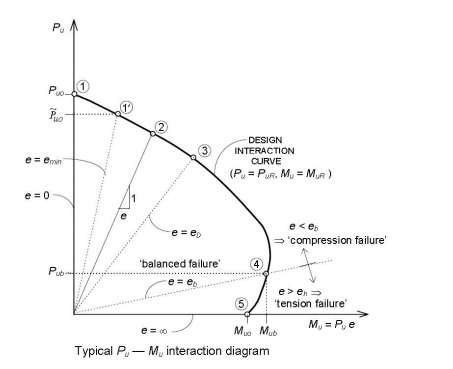
Typical interaction curve

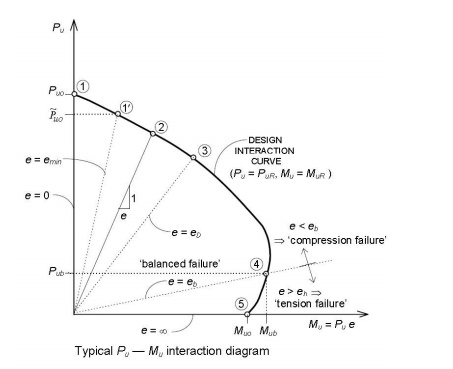
Salient Points on the Interaction Curve

The salient points, marked 1 to 5 on the interaction curve correspond to the failure strain profiles, marked 1 to 5 in the above figure.

•      The point 1 in figure corresponds to the condition of axial loading with e = 0. For this case of 'pure' axial compression.

•      The point 1¹ in figure corresponds to the condition of axial loading with the mandatory minimum eccentricity e_min prescribed by the Code.

•      The point 3 in figure corresponds to the condition x_u = D, i.e., e = e_D. For e < e_D, the

entire section is under compression and the neutral axis is located outside the section (x_u > D), with 0.002 < ?_cu < 0.0035. For e > e_D, the NA is located within the section (x_u < D) and ?_cu = 0.0035 at the 'highly compressed edge'.

•      The point 4 in figure corresponds to the balanced failure condition, with e = e_b and x_u = x_{u, b} . The design strength values for this 'balanced failure' condition are denoted as

P_ub and M_ub.

The point 5 in figure corresponds to a 'pure' bending condition (e = ?, P_uR = 0); the resulting ultimate moment of resistance is denoted M_uo and the corresponding NA depth takes on a minimum value x_{u, min}.