The Data Encryption Standard

THE DATA ENCRYPTION STANDARD     

The most widely used encryption scheme is based on the Data Encryption Standard (DES) adopted in 1977 by the National Bureau of Standards, now the National Institute of Standards and Technology (NIST), as Federal Information Processing Standard 46 (FIPS PUB 46). The algorithm itself is referred to as the Data Encryption Algorithm (DEA).7 For DES, data are encrypted in 64-bit blocks using a 56-bit key. The algorithm transforms 64-bit input in a series of steps into a 64-bit output. The same steps, with the same key, are used to reverse the encryption.

The DES enjoys widespread use. It has also been the subject of much controversy concerning how secure the DES is. To appreciate the nature of the controversy, let us quickly review the history of the DES.

In the late 1960s, IBM set up a research project in computer cryptography led by Horst Feistel. The project concluded in 1971 with the development of an algorithm with the designation LUCIFER [FEIS73], which was sold to Lloyd’s of London for use in a cash-dispensing system, also developed by IBM. LUCIFER is a Feistel block cipher that operates on blocks of 64 bits, using a key size of 128 bits. Because of the promising results produced by the LUCIFER project, IBM embarked on an effort to develop a marketable commercial encryption product that ideally could be imple- mented on a single chip. The effort was headed by Walter Tuchman and Carl Meyer, and it involved not only IBM researchers but also outside consultants and technical advice from the National Security Agency (NSA). The outcome of this effort was a refined version of LUCIFER that was more resistant to cryptanalysis but that had a reduced key size of 56 bits, in order to fit on a single chip.

In 1973, the National Bureau of Standards (NBS) issued a request for proposals for a national cipher standard. IBM submitted the results of its Tuchman–Meyer project. This was by far the best algorithm proposed and was adopted in 1977 as the Data Encryption Standard.

Before its adoption as a standard, the proposed DES was subjected to intense criticism, which has not subsided to this day. Two areas drew the critics’ fire. First, the key length in IBM’s original LUCIFER algorithm was 128 bits, but that of the proposed system was only 56 bits, an enormous reduction in key size of 72 bits. Critics feared that this key length was too short to withstand brute-force attacks. The second area of concern was that the design criteria for the internal structure of DES, the S-boxes, were classified. Thus, users could not be sure that the internal structure of DES was free of any hidden weak points that would enable NSA to decipher messages without benefit of the key. Subsequent events, particularly the recent work on differential cryptanalysis, seem to indicate that DES has a very strong internal structure. Furthermore, according to IBM participants, the only changes that were made to the proposal were changes to the S-boxes, suggested by NSA, that removed vulnerabilities identified in the course of the evaluation process.

Whatever the merits of the case, DES has flourished and is widely used, especially in financial applications. In 1994, NIST reaffirmed DES for federal use for another five years; NIST recommended the use of DES for applications other than the protection of classified information. In 1999, NIST issued a new version of its standard (FIPS PUB 46-3) that indicated that DES should be used only for legacy systems and that triple DES (which in essence involves repeating the DES algorithm three times on the plain- text using two or three different keys to produce the ciphertext) be used.We study triple DES in Chapter 6. Because the underlying encryption and decryption algorithms are the same for DES and triple DES, it remains important to understand the DES cipher.

DES Encryption

The overall scheme for DES encryption is illustrated in Figure 3.5. As with any encryption scheme, there are two inputs to the encryption function: the plaintext to be encrypted and the key. In this case, the plaintext must be 64 bits in length and the key is 56 bits in length.

Looking at the left-hand side of the figure, we can see that the processing of the plaintext proceeds in three phases. First, the 64-bit plaintext passes through an initial permutation (IP) that rearranges the bits to produce the permuted input. This is followed by a phase consisting of sixteen rounds of the same function, which involves both permutation and substitution functions. The output of the last (sixteenth) round consists of 64 bits that are a function of the input plaintext and the key. The left and right halves of the output are swapped to produce the preoutput. Finally, the preoutput is passed through a permutation [IP-1] that is the inverse of the initial permutation function, to produce the 64-bit ciphertext. With the exception of the initial and final permutations, DES has the exact structure of a Feistel cipher, as shown in Figure 3.3.

The right-hand portion of Figure 3.5 shows the way in which the 56-bit key is used. Initially, the key is passed through a permutation function. Then, for each of the sixteen rounds, a subkey (Ki ) is produced by the combination of a    left circular shift and a permutation. The permutation function is the same for each round, but a different subkey is produced because of the repeated shifts of the key bits.

INITIAL  PERMUTATION  The initial permutation and its inverse are defined by tables,  as shown in Tables 3.2a and 3.2b, respectively. The tables are to be interpreted as follows. The input to a table consists of 64 bits numbered from 1 to 64. The 64 entries in the permutation table contain a permutation of the numbers from 1 to 64. Each

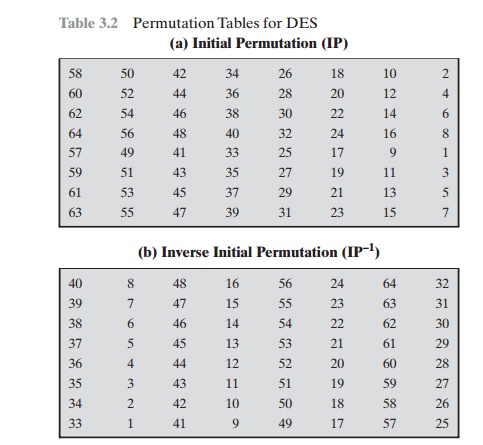
entry in the permutation table indicates the position of a numbered input bit in the output, which also consists of 64 bits.

To see that these two permutation functions are indeed the inverse of each other, consider the following 64-bit input M:

If we then take the inverse permutation Y = IP-1(X) = IP-1(IP(M)), it can be seen that the original ordering of the bits is restored.

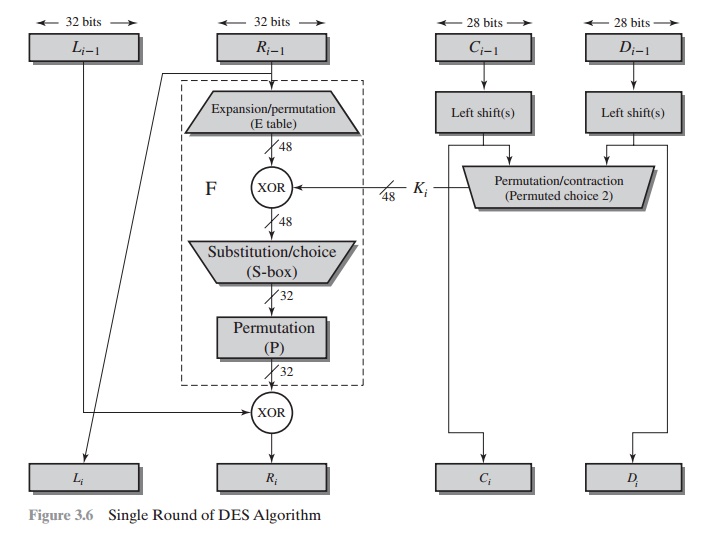
DETAILS OF SINGLE ROUND Figure 3.6 shows the internal structure of a single round. Again, begin by focusing on the left-hand side of the diagram. The left and right halves of  each   64-bit   intermediate   value   are   treated   as   separate   32-bit quantities, labeled L (left) and R (right). As in any classic Feistel cipher, the overall processing at each round can be summarized in the following formulas:

Li = Ri - 1

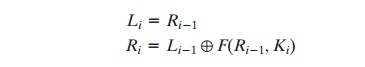
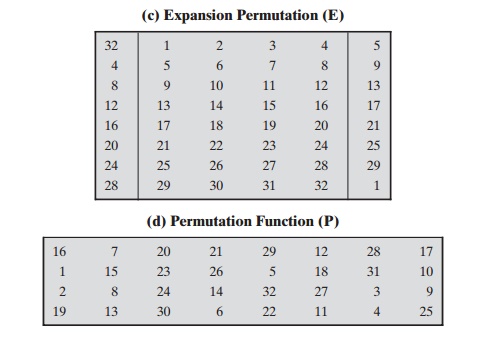
The round key Ki is 48 bits. The R input is 32 bits. This R input is first expanded to 48 bits by using a table that defines a permutation plus an expansion that involves duplication of 16 of the R bits (Table 3.2c). The resulting 48 bits are XORed with Ki . This 48-bit result passes through a substitution function that produces a 32-bit output, which is permuted as defined by Table 3.2d.

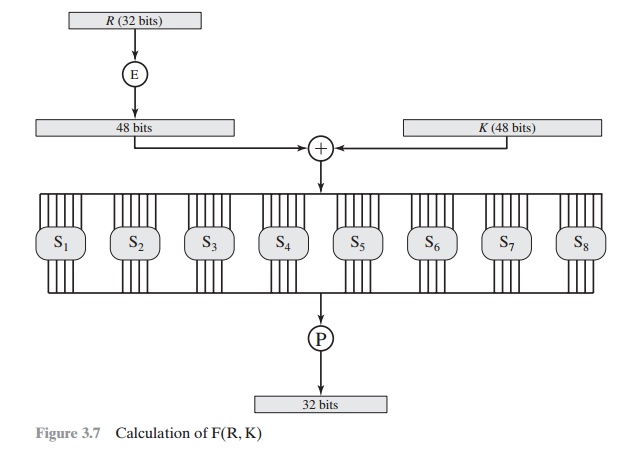
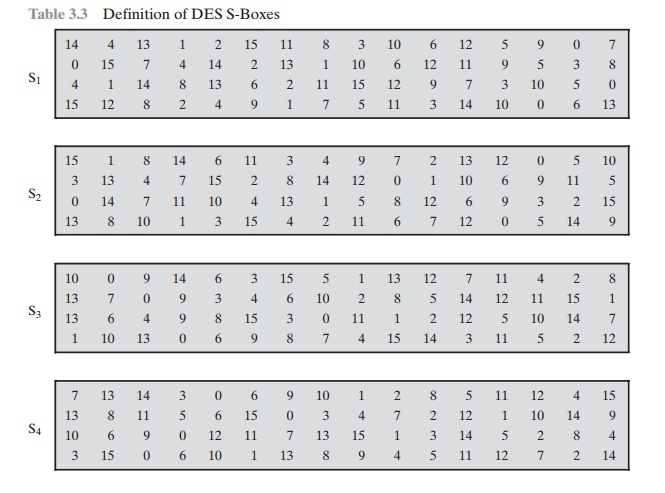
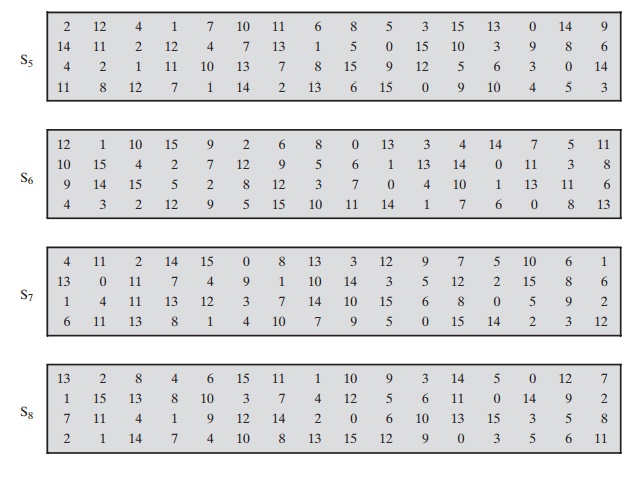
The role of the S-boxes in the function F is illustrated in Figure 3.7. The substi- tution consists of a set of eight S-boxes, each of which accepts 6 bits as input and produces 4 bits as output. These transformations are defined in Table 3.3, which is

interpreted as follows: The first and last bits of the input to box Si form a 2-bit binary number to select one of four substitutions defined by the four rows in the table for Si. The middle four bits select one of the sixteen columns. The decimal value in the cell selected by the row and column is then converted to its 4-bit representation to pro- duce the output. For example, in S1, for input 011001, the row is 01 (row 1) and the column is 1100 (column 12). The value in row 1, column 12 is 9, so the output is 1001.

Each row of an S-box defines a general reversible substitution. Figure 3.2 may be useful in understanding the mapping. The figure shows the substitution for row 0 of box S1.

The operation of the S-boxes is worth further comment. Ignore for the moment

the contribution of the key (Ki ). If you examine the expansion table, you see that the 32 bits of input are split into groups of 4 bits and then become groups of 6 bits by taking the outer bits from the two adjacent groups. For example, if part of the input word is

... efgh ijkl mnop ...

this becomes

... defghi hijklm lmnopq ...

The outer two bits of each group select one of four possible substitutions (one row of an S-box). Then a 4-bit output value is substituted for the particular 4-bit input (the middle four input bits). The 32-bit output from the eight S-boxes is then permuted, so that on the next round, the output from each S-box immediately affects as many others as possible.

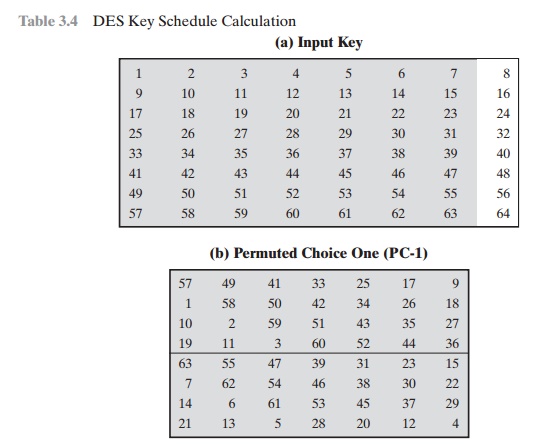
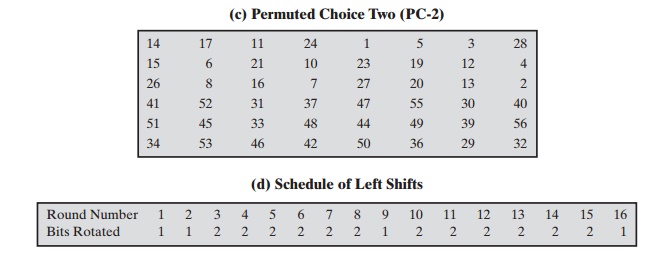
KEY GENERATION Returning to Figures 3.5 and 3.6, we see that a 64-bit key is used as input to the algorithm. The bits of the key are numbered from 1 through 64; every eighth bit is ignored, as indicated by the lack of shading in Table 3.4a. The key is first subjected to a permutation governed by a table labeled Permuted Choice One (Table 3.4b). The resulting 56-bit key is then treated as two 28-bit quantities, labeled C0 and D0. At each round, Ci - 1 and Di - 1 are separately subjected to a circular left shift or (rotation) of 1 or 2 bits, as governed by Table 3.4d. These shifted values serve as input to the next round. They also serve as input to the part labeled Permuted Choice Two (Table 3.4c), which produces a 48-bit output that serves as input to the function F(Ri - 1, Ki).

DES Decryption

As with any Feistel cipher, decryption uses the same algorithm as encryption, except that the application of the subkeys is reversed.

\