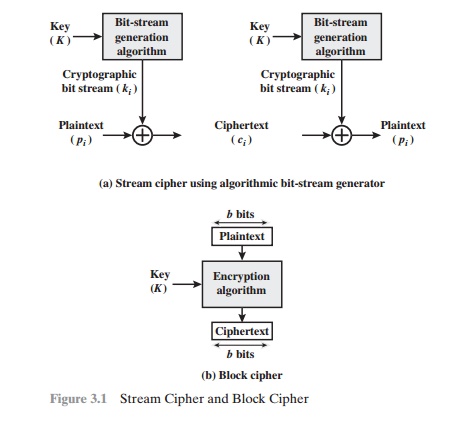
Chapter: Cryptography and Network Security Principles and Practice : One Symmetric Ciphers : Block Ciphers and the Data Encryption Standard
Block Cipher Principles
BLOCK CIPHER PRINCIPLES
Many
symmetric block encryption algorithms in current use are based on a structure referred to as a Feistel block cipher
[FEIS73]. For that reason, it is important to examine the design principles of
the Feistel cipher. We begin with a comparison of stream ciphers and block
ciphers. Then we discuss the motivation for the Feistel block cipher structure.
Finally, we discuss some of its implications.
Stream Ciphers and Block Ciphers
A
stream cipher is one that encrypts a digital data stream one bit or one byte at
a time. Examples of classical stream ciphers are the autokeyed Vigenère cipher
and the Vernam cipher. In the ideal case, a one-time pad version of the Vernam
cipher would be used (Figure 2.7), in which the keystream (ki) is as long as
the plaintext bit stream ( pi). If the cryptographic keystream is random, then
this cipher is unbreakable by any means other than acquiring the keystream.
However, the keystream must be provided to both users in advance via some
independent and secure channel. This introduces insurmountable logistical
problems if the intended data traffic is very large.
Accordingly,
for practical reasons, the bit-stream generator must be imple- mented as an
algorithmic procedure, so that the cryptographic bit stream can be produced by
both users. In this approach (Figure 3.1a), the bit-stream generator is a
key-controlled algorithm and must produce a bit stream that is
cryptographically strong. Now, the two users need only share the generating
key, and each can produce the keystream.
A
block cipher is one in which a block of plaintext is treated as a whole and
used to produce a ciphertext block of equal length. Typically, a block size of
64 or 128 bits is used. As with a stream cipher, the two users share a
symmetric encryption key (Figure 3.1b). Using some of the modes of operation
explained in Chapter 6, a block cipher can be used to achieve the same effect
as a stream cipher.
Far
more effort has gone into analyzing block ciphers. In general, they seem
applicable to a broader range of applications than stream ciphers. The vast
majority of network-based symmetric cryptographic applications make use of
block ciphers. Accordingly, the concern in this chapter, and in our discussions
throughout the book of symmetric encryption, will primarily focus on block
ciphers.
Motivation for
the Feistel Cipher Structure
A
block cipher operates on a plaintext block of n bits to produce a
ciphertext block of
n bits. There
are 2n possible different
plaintext blocks and, for
the encryption to be reversible (i.e., for decryption to be possible),
each must
produce a unique ciphertext block. Such a
transformation is called reversible, or nonsingular. The following examples
illustrate nonsingular and singular transfor- mations for n = 2.

In the latter case, a ciphertext of 01 could have been produced by one of two plain- text blocks. So if we limit ourselves to reversible mappings, the number of different transformations is 2n!.2
Figure 3.2 illustrates the logic of a
general substitution cipher for n = 4.
A
4-bit input produces one of 16 possible input states, which is mapped by the substitution cipher into a unique one of
16 possible output states, each of
which is represented by 4 ciphertext bits. The encryption and decryption
mappings can be
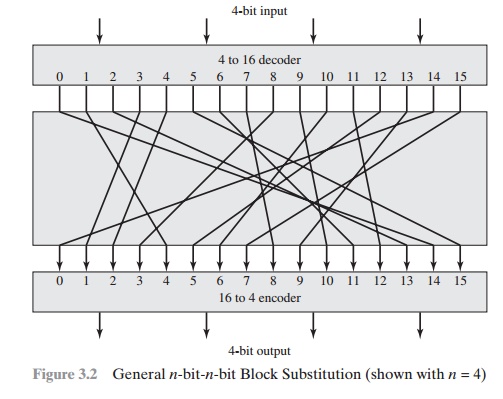
defined by a tabulation, as shown in Table 3.1. This is the most general form of block cipher and can be used to define
any reversible mapping between plaintext and ciphertext. Feistel refers
to this as the ideal block cipher, because it allows
for the max- imum number of possible encryption mappings from
the plaintext block
[FEIS75].
But there is a practical problem with the
ideal block cipher. If a small block size, such as n = 4, is used, then the system is equivalent to a classical
substitution cipher. Such systems, as we have seen, are vulnerable to a statistical analysis of the plaintext. This weakness is not inherent in the use of a substitution
cipher but rather results from
the use of a small block size. If n is sufficiently
large and an arbitrary reversible substitution between plaintext and ciphertext
is allowed, then the statistical characteristics of the source plaintext are
masked to such an extent that this
type of cryptanalysis is infeasible.
An arbitrary reversible substitution cipher
(the ideal block cipher) for a large
block size is not practical, however, from an implementation and performance point of
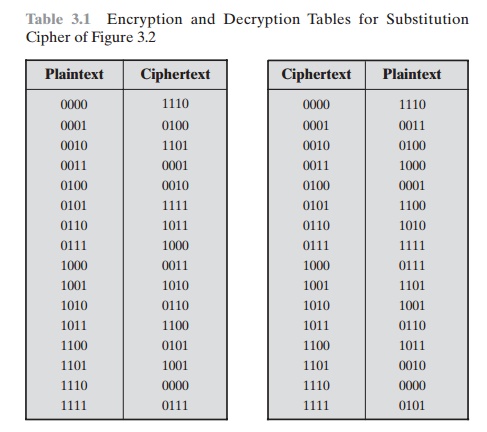
view. For such a transformation, the mapping itself constitutes the key. Consider
again Table 3.1, which defines one
particular reversible mapping from plaintext
to ciphertext for n = 4. The mapping can
be defined by the entries
in the second column, which show the value of the ciphertext for each
plaintext block. This, in essence,
is the key that determines the specific mapping from among all possible
mappings. In this case, using this straightforward method of defining the key, the required key length is (4 bits) * (16 rows) = 64 bits. In general,
for an n-bit ideal block cipher, the length of the key defined in this fashion
is n * 2n bits. For a 64-bit block,
which is a desirable length to
thwart statistical attacks, the required key length is
64 * 264 = 270 ~~ 1021 bits.
In considering these difficulties, Feistel
points out that what is needed is an approximation to the ideal block cipher
system for large n, built up out of
compo- nents that are easily realizable [FEIS75]. But before turning to
Feistel’s approach, let us make one other observation. We could use the general block substitution cipher but, to make its implementation tractable, confine ourselves to a subset
of the 2n! possible reversible
mappings. For example, suppose we
define the mapping in terms of a set of linear equations. In the case of n = 4, we have
y1 = k11x1 + k12x2 + k13x3 + k14x4 y2 = k21x1 + k22x2 + k23x3 + k24x4 y3 = k31x1 + k32x2 + k33x3 + k34x4 y4 = k41x1 + k42x2 + k43x3 + k44x4
where the xi are the four binary
digits of the plaintext block, the
yi are the four binary
digits of the ciphertext block, the
kij are the binary coefficients,
and arith- metic is mod 2. The key size is
just n2, in this case 16
bits. The danger with this kind of formulation
is that it may be vulnerable to cryptanalysis
by an attacker that
is aware of the structure of the algorithm. In this example,
what we have is essentially the Hill cipher discussed in Chapter
2, applied to binary data
rather than characters. As we saw in Chapter 2, a simple linear system such as this is quite
vulnerable.
The Feistel Cipher
Feistel proposed [FEIS73]
that we can approximate the ideal block
cipher by utilizing the concept of a product cipher, which
is the execution of two or more simple ciphers in sequence in such
a way that the final
result or product
is cryptographically stronger than any of the component ciphers. The essence
of the approach is to develop a block
cipher with a key length
of k bits and a block
length of n bits, allowing a total of 2k possible transformations, rather than the 2n! transformations available with the ideal block cipher.
In particular, Feistel
proposed the use of a cipher that alternates substitutions and permutations, where these
terms are defined
as follows:
Substitution: Each plaintext element or group of elements is uniquely replaced by a corresponding ciphertext element or group
of elements.
Permutation: A sequence of plaintext elements
is replaced by a permutation of that sequence. That is, no elements are added or deleted or
replaced in the sequence, rather the order in which the elements appear in the
sequence is changed.
In fact, Feistel’s
is a practical application of a proposal
by Claude Shannon
to develop a product cipher that alternates confusion and diffusion functions [SHAN49].3 We look next at these concepts
of diffusion and confusion and then present the Feistel
cipher. But first,
it is worth commenting on this remarkable fact: The Feistel
cipher structure, which dates back over a quarter century
and which, in turn,
is based on Shannon’s proposal
of 1945, is the structure
used by many signifi- cant symmetric block ciphers currently in use.
DIFFUSION AND CONFUSION The terms diffusion and confusion were introduced by Claude Shannon to capture the two basic building blocks for any cryptographic system [SHAN49]. Shannon’s concern was to thwart cryptanalysis based on statistical analysis. The reasoning is as follows. Assume the attacker has some knowledge of the statistical characteristics of the plaintext. For example, in a human-readable message in some language, the frequency distribution of the various letters may be known. Or there may be words or phrases likely to appear in the message (probable words). If these statistics are in any way reflected in the ciphertext, the cryptanalyst may be able to deduce the encryption key, part of the key, or at least a set of keys likely to contain the exact key. In what Shannon refers to as a strongly ideal cipher, all statistics of the ciphertext are independent of the particular key used. The arbitrary substitution cipher that we discussed previously (Figure 3.2) is such a cipher, but as we have seen, it is impractical.4
Other than recourse to ideal systems,
Shannon suggests two methods for frus- trating statistical cryptanalysis:
diffusion and confusion. In diffusion,
the statistical structure of the plaintext is dissipated into long-range
statistics of the ciphertext. This is
achieved by having each plaintext digit affect the value of many ciphertext
digits; generally, this is equivalent to having each ciphertext digit
be affected by many plaintext
digits. An example of
diffusion is to
encrypt a message M = m1, m2, m3, ... of characters with an averaging operation:
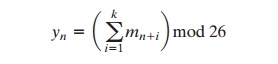
adding k successive letters to get a ciphertext letter yn. One can show that the statis- tical structure of the plaintext has been dissipated. Thus, the letter frequencies in the ciphertext will be more nearly equal than in the plaintext; the digram frequencies will also be more nearly equal, and so on. In a binary block cipher, diffusion can be achieved by repeatedly performing some permutation on the data followed by applying a function to that permutation; the effect is that bits from different positions in the original plaintext contribute to a single bit of ciphertext.5
Every block cipher involves a transformation
of a block of plaintext into a block of ciphertext, where the transformation
depends on the key. The mechanism of diffusion seeks to make
the statistical relationship between the plaintext and ciphertext as complex
as possible in order to thwart attempts
to deduce the key. On
the other hand, confusion seeks to
make the relationship between the statistics of the ciphertext and the value of
the encryption key as complex as possible,
again to thwart attempts to discover the key. Thus, even if the
attacker can get some handle on the statistics of the ciphertext, the way in which the key was used to produce that ciphertext is so complex
as to make it difficult to deduce the key. This is achieved by the
use of a complex substitution algorithm. In contrast,
a simple linear substitution
function would add little confusion.
As [ROBS95b] points
out, so successful are diffusion and confusion in captur-
ing the essence of the desired attributes of a block
cipher that they have become
the cornerstone of modern
block cipher design.
FEISTEL CIPHER STRUCTURE
The left-hand side of
Figure 3.3 depicts the structure proposed by Feistel.
The inputs to the encryption algorithm are a plaintext block of length 2w bits and a key K. The plaintext block
is divided into two halves, L0 and R0. The two halves of the data pass through
n rounds of processing and then combine
to produce the ciphertext block. Each round i has as inputs Li - 1 and Ri - 1 derived from the previous round, as well as a
subkey Ki derived from the overall K. In
general, the subkeys Ki are different from K and from each other. In Figure 3.3, 16 rounds are used, although any number of rounds could be implemented.
All rounds have the same structure. A substitution is performed on the left
half of the data. This is done by applying
a round function F to the right half of the data and then taking the exclusive-OR
of the output of that function and the left half of the data. The round function has the same general
structure for each round but is parameterized by the round subkey
Ki . Another
way to express this is to say that F is a function of right-half
block of w bits and a subkey of y bits, which pro- duces an output value
of length w bits: F(REi, Ki + 1). Following
this substitution, a

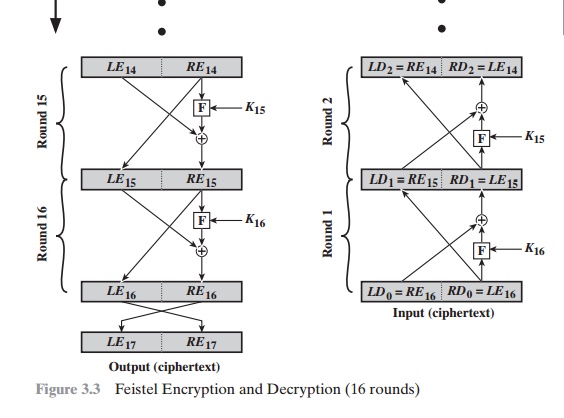
permutation is performed that consists of the interchange of the two halves of the
data.6 This structure is a
particular form of the substitution-permutation network (SPN) proposed by Shannon.
The exact realization of a Feistel
network depends on the choice of the following
parameters and design features:
Block size: Larger
block sizes mean greater security (all other things being equal) but reduced
encryption/decryption speed for a given algorithm. The greater security
is achieved by greater diffusion. Traditionally, a block size of
64 bits has been considered a reasonable tradeoff
and was nearly universal in block
cipher design. However, the new AES uses a 128-bit block
size.
Key size: Larger key size means
greater security but may decrease
encryption/ decryption speed. The
greater security is achieved by greater resistance to brute-force attacks
and greater confusion. Key sizes of 64 bits or less are now widely considered to be inadequate, and 128 bits has become
a common size.
Number of rounds: The
essence of the Feistel cipher is that a single round offers inadequate security
but that multiple rounds offer increasing security. A typical size is 16 rounds.
Subkey generation algorithm:
Greater
complexity in this algorithm should lead
to greater difficulty of cryptanalysis.
Round function F: Again, greater complexity generally means greater
resistance to cryptanalysis.
There are two other considerations in the
design of a Feistel cipher:
Fast software encryption/decryption: In many cases, encryption is embedded in
applications or utility functions in such a way as to preclude a hardware implementation. Accordingly, the speed of
execution of the algorithm becomes a concern.
Ease of analysis: Although we would like
to make our
algorithm as difficult as possible to cryptanalyze, there is great
benefit in making
the algorithm easy to
analyze. That is, if the algorithm
can be concisely and clearly explained, it is easier to analyze that algorithm for cryptanalytic vulnerabilities and therefore develop a higher level of assurance
as to its strength. DES, for example, does not
have an easily
analyzed functionality.
FEISTEL DECRYPTION ALGORITHM The process of decryption with a Feistel
cipher is essentially the same as the encryption
process. The rule is as follows: Use the ciphertext as input to the algorithm, but use the subkeys Ki in reverse order.
That is, use Kn in the first round,
Kn - 1 in the second
round, and so on, until
K1 is used in the
last round. This is a nice feature, because it means we need not implement
two different algorithms; one for encryption and one for decryption.
To see that the same algorithm with a reversed
key order produces
the correct result, Figure 3.3
shows the encryption process going down the left-hand side and the decryption
process going up the right-hand side for a 16-round algorithm. For clarity,
we use the notation LEi and REi for data traveling through the encryption algorithm and LDi and RDi for data traveling through
the decryption algorithm. The diagram
indicates that, at every round,
the intermediate value of the decryption
process is equal to the corresponding value of the encryption process with the two halves
of the value swapped. To put this another way, let the output of the ith encryption round
be LEi 7 REi (LEi concatenated with REi). Then the corresponding output of the (16
– i)th decryption round
is REi 7 LEi or, equivalently, LD16 - i 7 RD16
- i.
Let us walk through Figure 3.3 to demonstrate
the validity of the preceding assertions. After the last
iteration of the encryption process, the two halves of the output are swapped,
so that the ciphertext is RE167 LE16. The output of that round is the
ciphertext. Now take that ciphertext and use it as input to the same algorithm.
The input to the first round is RE16 7 LE16, which is equal to
the 32-bit swap of the output of the sixteenth round of the encryption process.
Now we would like to show that the output of the first round of the decryption
process is equal to a 32-bit swap of the input to the sixteenth
round of the encryption
process. First, consider the encryption process. We see that

Thus, we have
LD1 = RE15 and RD1 = LE15. Therefore, the output of the first round
of the decryption process is RE15 7 LE15, which
is the 32-bit swap of the input to the sixteenth round of the
encryption. This correspondence holds all the way
through the 16 iterations, as is easily
shown. We can cast this process in general terms. For the ith iteration
of the encryption algorithm,
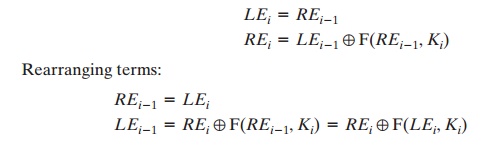
Thus, we have described the inputs
to the ith iteration as a function
of the outputs, and these equations confirm the assignments shown in the right-hand side of Figure 3.3.
Finally, we see that the output of the last round of the decryption
process is
RE0 || LE0. A 32-bit swap
recovers the original plaintext, demonstrating the validity of the Feistel decryption process.
Note that the derivation does not require
that F be a reversible function. To see this, take a limiting case in which F
produces a constant output (e.g., all ones) regardless of the values of its two
arguments. The equations still hold.
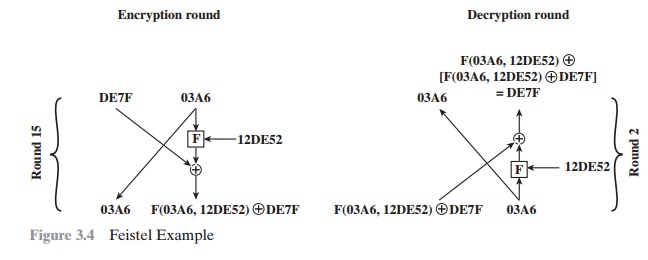
To help clarify the preceding concepts, let us look at a specific example (Figure 3.4) and focus on
the fifteenth round of encryption,
corresponding to the second
round of decryption. Suppose
that the blocks at each stage are 32 bits (two 16-bit halves) and that the key size is 24 bits.
Suppose that at the end of encryption round fourteen, the value of the
intermediate block (in hexadecimal) is DE7F03A6. Then LE14 = DE7F and RE14 = 03A6. Also assume that
the value of K15 is 12DE52.
After round 15, we have LE15 = 03A6 and RE15
= F(03A6, 12DE52) NOR DE7F.
Now let’s look at the decryption. We assume
that LD1 = RE15 and RD1 = LE15, as
shown in Figure
3.3, and we
want to demonstrate
that LD2 = RE14 and RD2 = LE14.
So, we start with LD1 = F(03A6, 12DE52) NOR DE7F and RD1 = 03A6.
Then,
from Figure 3.3, LD2 =
03A6 = RE14 and RD2 = F(03A6, 12DE52)
NOR [F(03A6, 12DE52) { DE7F]= DE7F = LE14.
Related Topics