The Bitwise Operators - Java

The Bitwise Operators

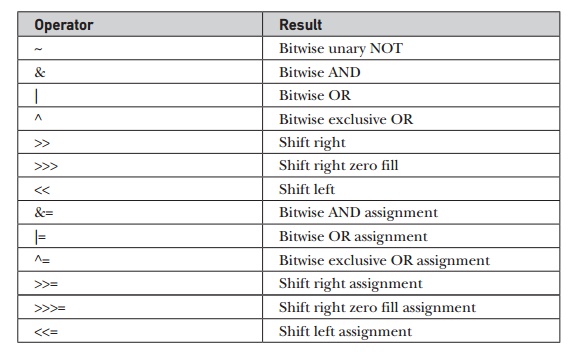
Java defines several bitwise operators that can be applied to the integer types: long, int, short, char, and byte. These operators act upon the individual bits of their operands. They are summarized in the following table:

Since the bitwise operators manipulate the bits within an integer: it is important to understand what effects such manipulations may have on a value. Specifically, it is useful to know how Java stores integer values and how it represents negative numbers. So, before continuing, let’s briefly review these two topics.

All of the integer types are represented by binary numbers of varying bit widths. For example, the byte value for 42 in binary is 00101010, where each position represents a power of two, starting with 2⁰ at the rightmost bit. The next bit position to the left would be 2¹, or 2, continuing toward the left with 2², or 4, then 8, 16, 32, and so on. So 42 has 1 bits set at positions 1, 3, and 5 (counting from 0 at the right); thus, 42 is the sum of 2¹ + 2³ + 2⁵, which is 2 + 8 + 32.

All of the integer types (except char) are signed integers. This means that they can represent negative values as well as positive ones. Java uses an encoding known as two’s complement, which means that negative numbers are represented by inverting (changing 1’s to 0’s and vice versa) all of the bits in a value, then adding 1 to the result. For example, –42 is represented by inverting all of the bits in 42, or 00101010, which yields 11010101, then adding 1, which results in 11010110, or –42. To decode a negative number, first invert all of the bits, then add 1. For example, –42, or 11010110 inverted, yields 00101001, or 41, so when you add 1 you get 42.

The reason Java (and most other computer languages) uses two’s complement is easy to see when you consider the issue of zero crossing. Assuming a byte value, zero is represented by 00000000. In one’s complement, simply inverting all of the bits creates 11111111, which creates negative zero. The trouble is that negative zero is invalid in integer math. This problem is solved by using two’s complement to represent negative values. When using two’s complement, 1 is added to the complement, producing 100000000. This produces a 1 bit too far to the left to fit back into the byte value, resulting in the desired behavior, where –0 is the same as 0, and 11111111 is the encoding for –1. Although we used a byte value in the preceding example, the same basic principle applies to all of Java’s integer types.

Because Java uses two’s complement to store negative numbers—and because all integers are signed values in Java—applying the bitwise operators can easily produce unexpected results. For example, turning on the high-order bit will cause the resulting value to be interpreted as a negative number, whether this is what you intended or not. To avoid unpleasant surprises, just remember that the high-order bit determines the sign of an integer no matter how that high-order bit gets set.

The Bitwise Logical Operators

The bitwise logical operators are &, |, ^, and ~. The following table shows the outcome of each operation. In the discussion that follows, keep in mind that the bitwise operators are applied to each individual bit within each operand.

The Bitwise NOT

Also called the bitwise complement, the unary NOT operator, ~, inverts all of the bits of its operand. For example, the number 42, which has the following bit pattern:

00101010 becomes

11010101

after the NOT operator is applied.

The Bitwise AND

The AND operator, &, produces a 1 bit if both operands are also 1. A zero is produced in all other cases. Here is an example:

The Bitwise OR

The OR operator, |, combines bits such that if either of the bits in the operands is a 1, then the resultant bit is a 1, as shown here:

The Bitwise XOR

The XOR operator, ^, combines bits such that if exactly one operand is 1, then the result is 1. Otherwise, the result is zero. The following example shows the effect of the ^. This example also demonstrates a useful attribute of the XOR operation. Notice how the bit pattern of 42 is inverted wherever the second operand has a 1 bit. Wherever the second operand has a 0 bit, the first operand is unchanged. You will find this property useful when performing some types of bit manipulations.

Using the Bitwise Logical Operators

The following program demonstrates the bitwise logical operators:

// Demonstrate the bitwise logical operators.

// Demonstrate the bitwise logical operators.                         

class BitLogic {                                         

public static void main(String args[]) {                         

String binary[] = {                                               

"0000", "0001", "0010",         "0011", "0100",   "0101",       "0110",       "0111",

"1000", "1001", "1010",         "1011", "1100",   "1101",       "1110",       "1111"

};                                            

int a = 3; // 0 + 2 + 1 or 0011  in binary                       

int b = 6; // 4 + 2 + 0 or 0110  in binary                       

int c = a | b;                                      

int d = a & b;                                             

int e = a ^ b;                                               

int f = (~a & b)|(a & ~b);                                               

int g = ~a & 0x0f;                                      

System.out.println("      a =     " + binary[a]);               

System.out.println("      b =    " + binary[b]);               

System.out.println("      a|b =  " + binary[c]);               

System.out.println("      a&b =         " + binary[d]);               

System.out.println("      a^b = " + binary[e]);               

System.out.println("~a&b|a&~b =    " + binary[f]);                

System.out.println("      ~a =   " + binary[g]);               

}                                             

}                                             

In this example, a and b have bit patterns that present all four possibilities for two binary digits: 0-0, 0-1, 1-0, and 1-1. You can see how the | and & operate on each bit by the results in c and d. The values assigned to e and f are the same and illustrate how the ^ works. The string array named binary holds the human-readable, binary representation of the numbers 0 through 15. In this example, the array is indexed to show the binary representation of each result. The array is constructed such that the correct string representation of a binary value n is stored in binary[n]. The value of ~a is ANDed with 0x0f (0000 1111 in binary) in order to reduce its value to less than 16, so it can be printed by use of the binary array. Here is the output from this program:

a = 0011 b = 0110 a|b = 0111 a&b = 0010 a^b = 0101

~a&b|a&~b = 0101 ~a = 1100

The Left Shift

The left shift operator, <<, shifts all of the bits in a value to the left a specified number of times. It has this general form:

value << num

Here, num specifies the number of positions to left-shift the value in value. That is, the << moves all of the bits in the specified value to the left by the number of bit positions specified by num. For each shift left, the high-order bit is shifted out (and lost), and a zero is brought in on the right. This means that when a left shift is applied to an int operand, bits are lost once they are shifted past bit position 31. If the operand is a long, then bits are lost after bit position 63.

Java’s automatic type promotions produce unexpected results when you are shifting byte and short values. As you know, byte and short values are promoted to int when an expression is evaluated. Furthermore, the result of such an expression is also an int. This means that the outcome of a left shift on a byte or short value will be an int, and the bits shifted left will not be lost until they shift past bit position 31. Furthermore, a negative byte or short value will be sign-extended when it is promoted to int. Thus, the high-order bits will be filled with 1’s. For these reasons, to perform a left shift on a byte or short implies that you must discard the high-order bytes of the int result. For example, if you left-shift a byte value, that value will first be promoted to int and then shifted. This means that you must discard the top three bytes of the result if what you want is the result of a shifted byte value. The easiest way to do this is to simply cast the result back into a byte. The following program demonstrates this concept:

// Left shifting a byte value. class ByteShift {

public static void main(String args[]) { byte a = 64, b;

int i;

i = a << 2;

b = (byte) (a << 2);

System.out.println("Original value of a: " + a); System.out.println("i and b: " + i + " " + b);

}

}

The output generated by this program is shown here:

Original value of a: 64 i and b: 256 0

Since a is promoted to int for the purposes of evaluation, left-shifting the value 64 (0100 0000) twice results in i containing the value 256 (1 0000 0000). However, the value in b contains 0 because after the shift, the low-order byte is now zero. Its only 1 bit has been shifted out.

Since each left shift has the effect of doubling the original value, programmers frequently use this fact as an efficient alternative to multiplying by 2. But you need to watch out. If you shift a 1 bit into the high-order position (bit 31 or 63), the value will become negative. The following program illustrates this point:

// Left shifting as a quick way to multiply by 2. class MultByTwo {

public static void main(String args[]) { int i;

int num = 0xFFFFFFE;

for(i=0; i<4; i++) { num = num << 1;

System.out.println(num);

}

}

}

The program generates the following output:

536870908

1073741816

2147483632 -32

The starting value was carefully chosen so that after being shifted left 4 bit positions, it would produce –32. As you can see, when a 1 bit is shifted into bit 31, the number is interpreted as negative.

The Right Shift

The right shift operator, >>, shifts all of the bits in a value to the right a specified number of times. Its general form is shown here:

value >> num

Here, num specifies the number of positions to right-shift the value in value. That is, the >> moves all of the bits in the specified value to the right the number of bit positions specified by num.

The following code fragment shifts the value 32 to the right by two positions, resulting in a being set to 8:

int a = 32;

a = a >> 2; // a now contains 8

When a value has bits that are “shifted off,” those bits are lost. For example, the next code fragment shifts the value 35 to the right two positions, which causes the two low-order bits to be lost, resulting again in a being set to 8:

int a = 35;

a = a >> 2; // a contains 8

Looking at the same operation in binary shows more clearly how this happens:

00100011 35 >> 2 00001000 8

Each time you shift a value to the right, it divides that value by two—and discards any remainder. In some cases, you can take advantage of this for high-performance integer division by 2.

When you are shifting right, the top (leftmost) bits exposed by the right shift are filled in with the previous contents of the top bit. This is called sign extension and serves to preserve the sign of negative numbers when you shift them right. For example, –8 >> 1 is –4, which, in binary, is

11111000 –8 >> 1 11111100 –4

It is interesting to note that if you shift –1 right, the result always remains –1, since sign extension keeps bringing in more ones in the high-order bits.

Sometimes it is not desirable to sign-extend values when you are shifting them to the right. For example, the following program converts a byte value to its hexadecimal string representation. Notice that the shifted value is masked by ANDing it with 0x0f to discard any sign-extended bits so that the value can be used as an index into the array of hexadecimal characters.

// Masking sign    extension.   

class HexByte {        

static public void main(String args[])     {

char hex[] = {

'0', '1', '2', '3', '4', '5', '6',     '7',

'8', '9', 'a', 'b', 'c', 'd', 'e',     'f'

};       

byte b = (byte) 0xf1;

System.out.println("b = 0x" + hex[(b >> 4) & 0x0f] + hex[b & 0x0f]);

}

}

Here is the output of this program:

b = 0xf1

The Unsigned Right Shift

As you have just seen, the >> operator automatically fills the high-order bit with its previous contents each time a shift occurs. This preserves the sign of the value. However, sometimes this is undesirable. For example, if you are shifting something that does not represent a numeric value, you may not want sign extension to take place. This situation is common when you are working with pixel-based values and graphics. In these cases, you will generally want to shift a zero into the high-order bit no matter what its initial value was. This is known as an unsigned shift. To accomplish this, you will use Java’s unsigned, shift-right operator, >>>, which always shifts zeros into the high-order bit.

The following code fragment demonstrates the >>>. Here, a is set to –1, which sets all 32 bits to 1 in binary. This value is then shifted right 24 bits, filling the top 24 bits with zeros, ignoring normal sign extension. This sets a to 255.

int a = -1; a = a >>> 24;

Here is the same operation in binary form to further illustrate what is happening:

11111111 11111111 11111111 11111111          –1 in binary as an int

>>>24        

00000000 00000000 00000000 11111111          255 in binary as an int

The >>> operator is often not as useful as you might like, since it is only meaningful for 32- and 64-bit values. Remember, smaller values are automatically promoted to int in expressions. This means that sign-extension occurs and that the shift will take place on a 32-bit rather than on an 8- or 16-bit value. That is, one might expect an unsigned right shift on a byte value to zero-fill beginning at bit 7. But this is not the case, since it is a 32-bit value that is actually being shifted. The following program demonstrates this effect:

// Unsigned shifting        a        byte value.

class ByteUShift {                           

static public void  main(String args[]) {

char hex[] = {                         

'0',     '1', '2',         '3', '4',         '5', '6', '7',

'8',     '9', 'a',         'b', 'c',         'd', 'e', 'f'

};                                   

byte b         = (byte) 0xf1;      

byte c          = (byte) (b   >> 4);         

byte d         = (byte) (b   >>> 4);      

byte e          = (byte) ((b & 0xff) >> 4);

System.out.println("      b = 0x"

+ hex[(b >> 4)      &       0x0f] +        hex[b & 0x0f]);

System.out.println("      b >> 4 = 0x"

+ hex[(c >> 4)      &       0x0f] +        hex[c & 0x0f]);

System.out.println("      b >>> 4 = 0x"

+ hex[(d >> 4)      &       0x0f] +        hex[d & 0x0f]);

System.out.println("(b & 0xff) >> 4 = 0x" + hex[(e >> 4) & 0x0f] + hex[e & 0x0f]);

}

}

The following output of this program shows how the >>> operator appears to do nothing when dealing with bytes. The variable b is set to an arbitrary negative byte value for this demonstration. Then c is assigned the byte value of b shifted right by four, which is 0xff because of the expected sign extension. Then d is assigned the byte value of b unsigned shifted right by four, which you might have expected to be 0x0f, but is actually 0xff because of the sign extension that happened when b was promoted to int before the shift. The last expression sets e to the byte value of b masked to 8 bits using the AND operator, then shifted right by four, which produces the expected value of 0x0f. Notice that the unsigned shift right operator was not used for d, since the state of the sign bit after the AND was known.

b = 0xf1 b >> 4 = 0xff b >>> 4 = 0xff

(b & 0xff) >> 4 = 0x0f

Bitwise Operator Compound Assignments

All of the binary bitwise operators have a compound form similar to that of the algebraic operators, which combines the assignment with the bitwise operation. For example, the following two statements, which shift the value in a right by four bits, are equivalent:

a = a >> 4; a >>= 4;

Likewise, the following two statements, which result in a being assigned the bitwise expression a OR b, are equivalent:

a = a | b; a |= b;

The following program creates a few integer variables and then uses compound bitwise operator assignments to manipulate the variables:

class OpBitEquals {

public static void main(String args[]) { int a = 1;

int b = 2; int c = 3;

a |= 4; b >>= 1; c <<= 1; a ^= c;

System.out.println("a = " + a); System.out.println("b = " + b); System.out.println("c = " + c);

}

}

The output of this program is shown here:

a = 3 b = 1 c = 6