Systematic completion of lists

Systematic completion of lists

Suppose that you are already given a list that is partially filled. How would you complete it? In the activity with 4-digit numbers we had experienced this already. The idea is to find how the filled in part is arranged and use the same idea to complete the rest.

Try this

Form a group with two of your friends and try this. All three of you together have to draw a scene. First, one of your friends should draw one part, next the other friend has to continue it, and finally you have to complete it. No discussion or any other communication is allowed. Finally each person tells what (s) he actually intended to draw the full picture.

Completion with some constraints is best enjoyed in Sudoku. This is a puzzle where there is a partially filled in grid. Horizontal lines of cells in the grid are called as rows and vertical lines of cells in the grid are called as columns. You have to fill in the remaining blank cells with numbers from 1 to 9 so that no number repeats in a row, or in a column. In 3×3 Sudoku, you can use only the numbers from 1 to 3. In 4x4 Sudoku, you can use only the numbers from 1 to 4 and so on.

Sudoku

The word Sudoku comes from the Japanese language. Su means ‘number’ and Doku means ‘single’. It refers to the condition that each number is listed only once in each row, column, box etc. The modern version of this puzzle is said to have come from Howard Garns, a 74-year-old retired architect and freelance puzzle constructor from Indiana, USA and it was first published in 1979.

(i) 3×3 Sudoku

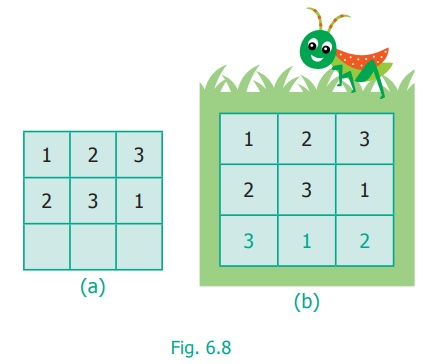
In Fig, 6.8 (a) two rows are fixed. We get only one possible way to complete the third row (Fig. 6.8 (b)).

(ii) 3×3 sudoku

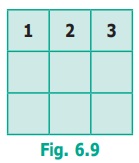
In the above 3 × 3 sudoku, the first row only is fixed. The second row can be filled in 2 ways either by 2 3 1 or 3 1 2

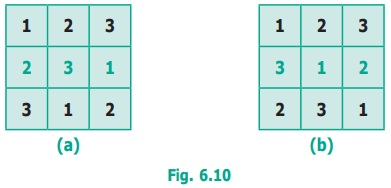
To fill the third row, bear in mind that numbers cannot be repeated in the row or in the column. The third row can be filled by only one way in each case.

(iii) 3 × 3 sudoku

In how many different ways can the first row be arranged?

The first row can be arranged in six ways as (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2) and (3,2,1).

(iv) Let us find all possible solutions to solve 3 × 3 sudoku puzzle.

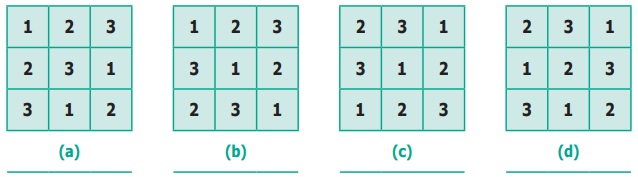
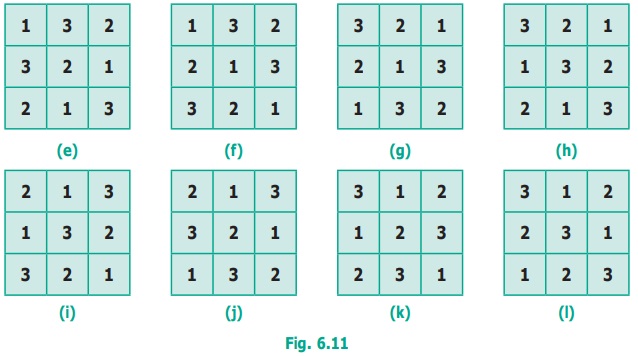
We get 12 possible ways.

(v) Here is a partially filled 4×4 sudoku.

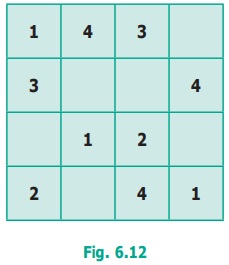
One way of completing it is given below. Is there any other way to complete the sudoku?

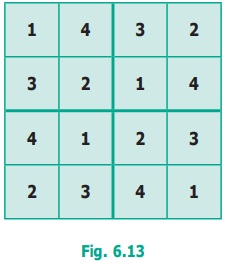
In the 4 × 4 Sudoku, there is an extra condition. We have four 2 × 2 grid boxes in the 4 × 4 sudoku. You have to be careful that no number from 1 to 4 repeats within that 2 × 2 grid also.