Relational Algebra in DBMS

Relational Algebra in DBMS

What is Relational Algebra?

Relational Algebra, was first created by Edgar F Codd while at IBM. It was used for modeling the data stored in relational databases and defining queries on it.

Relational Algebra is a procedural query language used to query the database tables using SQL.

Relational algebra operations are performed recursively on a relation (table) to yield an output. The output of these operations is a new relation, which might be formed by one or more input relations.

Relational Algebra is divided into various groups

Unary Relational Operations

SELECT ( symbol : σ)

PROJECT ( symbol : ∏)

Relational Algebra Operations from Set Theory

·        UNION (∪)

·        INTERSECTION (∩)

·        DIFFERENCE (−)

·        CARTESIAN PRODUCT (X)

SELECT (symbol : σ)

General form σ_c ( R ) with a relation R and a condition C on the attributes of R.

The SELECT operation is used for selecting a subset with tuples according to a given condition.

Select filters out all tuples that do not satisfy C.

STUDENT

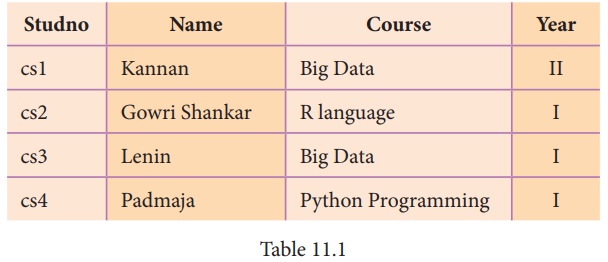
σ_course = “Big Data” (STUDENT )

PROJECT (symbol : Π)

The projection eliminates all attributes of the input relation but those mentioned in the projection list. The projection method defines a relation that contains a vertical subset of Relation.

Example 1

Π_course (STUDENT)

Result

Course

Big Data

R language

Python Programming

Example 2 (using Table 11.1)

Π_course (STUDENT)

Result

UNION (Symbol :∪)

It includes all tuples that are in tables A or in B. It also eliminates duplicates. Set A Union Set B would be expressed as A ∪ B

Example 3

Consider the following tables

Result

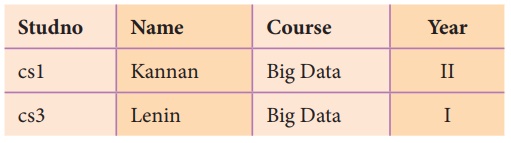
SET DIFFERENCE ( Symbol : - )

The result of A – B, is a relation which includes all tuples that are in A but not in B.

The attribute name of A has to match with the attribute name in B.

Example 4 ( using Table 11.2)

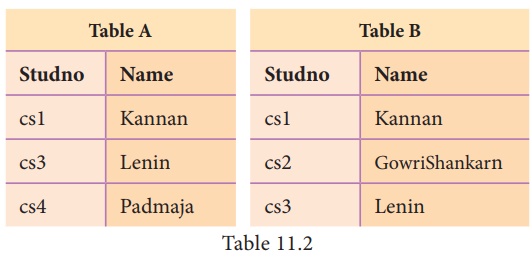
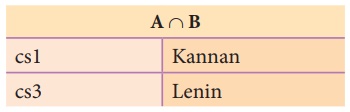
INTERSECTION (symbol : ∩)  A ∩ B

Defines a relation consisting of a set of all tuple that are in both in A and B. However, A and B must be union-compatible.

Example 5 (using Table 11.2)

PRODUCT OR CARTESIAN PRODUCT (Symbol : X )

Cross product is a way of combining two relations. The resulting relation contains, both relations being combined.

A x B means A times B, where the relation A and B have different attributes.

This type of operation is helpful to merge columns from two relations.

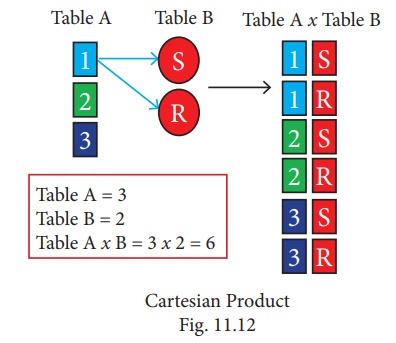
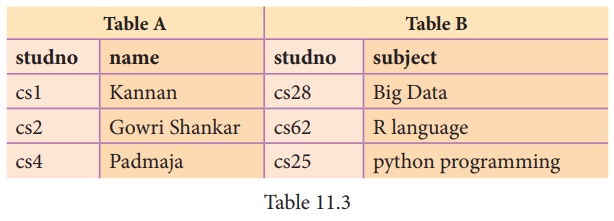
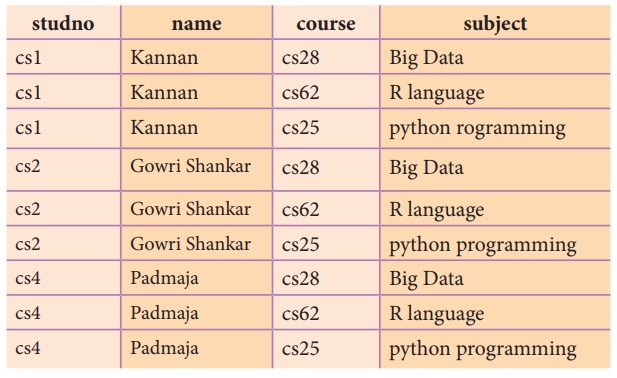
Cartesian product : Table A x Table B