Quantitative Analysis in Cellular Manufacturing

      QUANTITATIVE  ANALYSIS IN CELLULAR MANUFACTURING

A number of quantitative techniques have been developed to deal with problem areas in group technology and cellular manufacturing. In this section, we consider two problem areas: (1) grouping parts and machines into families, and (2) arranging machines in a GT cell. The first problem area has been and still is an active research area, and several of the more significant research publications are listed in our references . The technique we describe in the current section for salving the part and machine grouping problem is rank order clustering . The second problem area has also been the subject of research, and several reports are listed in the references. 

           Grouping Parts and Machines by Rank Order Clustering

The problem addressed here is to determine how machines in an existing plant should be grouped into machine cells. The problem is the same whether the cells are virtual or formal (Section 15.5.1 ).It is basically the problem of identifying part families. By identifying part families, the machines required in the cell to produce the part family can be properly selected. As previously discussed, the three basic methods to identify part families are (1) visual inspection, (2) parts classification and coding, and (3) production flow analysis.

The rank order clustering technique. first proposed by King [26J, is specifically applicable in production flow analysis. It is an efficient and easy-to-use algorithm for grouping machines into cells. In a starting part machine incidence matrix that might be compiled to document the part routings in a machine shop (or other job shop), the occupied locations in the matrix are organized in a seemingly random fashion. Rank order clustering works by reducing the part machine incidence matrix to a set of diagonalized blocks that represent part families and associated machine groups. Starting with the initial part machine incidence matrix. the algorithm consist, of the following steps:

   In each row of the matrix. read the series of ls and G's (blank entries = D's) from left to fight as a binary number. Rank the rows in 01 del uf decreasing value. In case of a tie, rank the rows in the same order as they appear in the current matrix

    Numbering from top to bottom, is the current order of rows the same as the rank order determined in the previous step? If yes, go to step 7, If no, go to the following step.

3, Reorder the rows in the part-machine incidence matrix by listing them in decreasing rank order, starting from the top

    In each column of the matrix. read the series of I 's and O's (blank entries = (j's) from top to bottom as a binary number. Rank the columns in order of decreasing value, In case of a tie. rank the columns in the same order as they appear in the current matrix.

    Numbering from left to right, is the current order of columns the same as the rank order determined in the previous step? If yes. go to step 7. If no. go to the following step.

    Reorder the columns in the part-machine incidence matrix by listing them in decreasing rank order, starting with the left column. Go to step I.

7 Stop

For readers unaccustomed to evaluating binary numbers in steps 1 and 4, it might be helpful to convert each binary value into its decimal equivalent (e.g., the entries in the first row of the matrix in Table 15.4 are read as 100100(10). This is converted into its decimal equivalent as follows: lx2⁸ + Ox2' + Ox2^b + 1x2⁵ + Ox2⁴ + Ox2³ + Ox2² + Ix2] + Ox2° = 256 + 32 + 2 = 290. It should be mentioned that decimal conversion becomes impractical for the large numbers of parts found in practice, and comparison of the binary numbers is preferred

EXAMPLE          15.3   Rank Order Clustering Technique

Apply the rank order clustering technique to the part-machine incidence matrix in Table 15.4

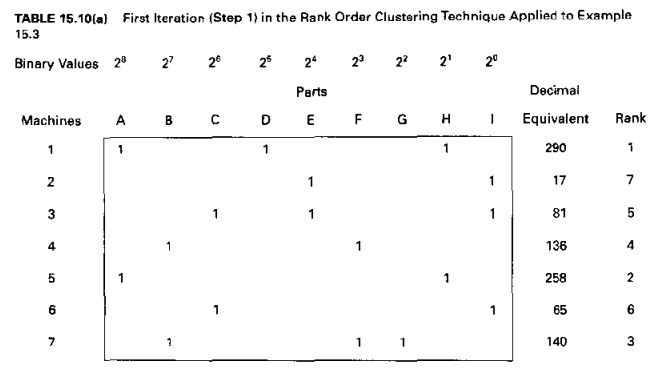
Solution: Step I consists of reading the series of 1's and D's in each row as a binary number. We have done this in Table 15.10(a). converting the binary value for each row to its decimal equivalent. The values are then rank ordered in the far right-hand column. In step 2. we see that the row order is different from the starting matrix. We therefore reorder the rows in step 3. In step 4, we read the series of I's and D's in each column from top to bottom as a binary number (again we have converted to the decimal equivalent, and the columns are ranked in order of decreasing value, as shown in Table 15.10(b).ln step 5, we see that the column order is different from the preceding matrix. Proceeding from step 6 back to steps 1 and 2, we see that a reordering of the columns provides a row order that is in descending value. and the algorithm is concluded (step 7). 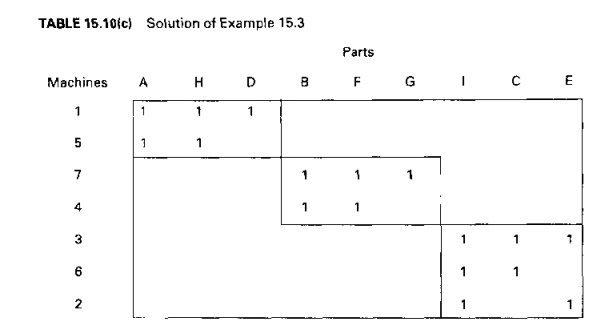The final solution  is shown in Table 15.10(c), A close comparison of this solution with Table 15,5 reveals that they are the carne part-machine groupings,

In the example problem, it was possible to divide the parts and machines into three mutually exclusive part-machine groups. This represents the ideal case because the part families and associated machine cells are completely segregated. However, it is not uncommon for there to be an overlap in processing requirements between machine groups That is, a given part type needs to be processed by more than one machine group. Let us illustrate this case and how the rank order clustering technique deals with it in the following example.

EXAMPLE       15.4     Overlapping Machine Requirements

Consider the part-machine incidence matrix in Table 15.11. This is the same as the original part-machine incidence matrix in Table 15.4 except that part B requires

processing on machines 1.4, and 7 (1 is the additional machine) and part D now requires processing on machines 1 and 4 (4 is the additional machine). Use the rank order clustering technique to arrange parts and machine into groups.

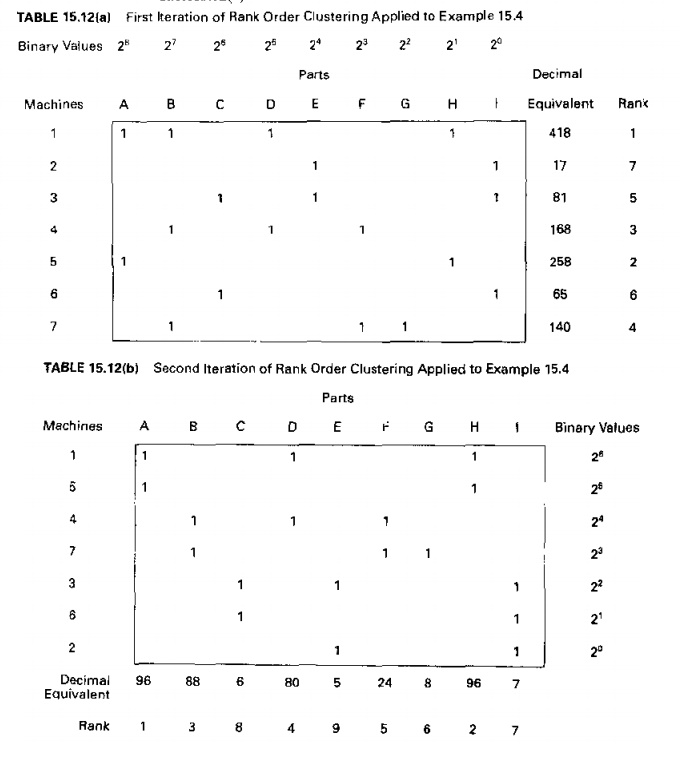
 Solution: The rank order clustering technique converges to a solution in two iterations, shown in Tables 15.12(a) and 15.l2(b), with the final solution shown in Table1.'l.12(c).

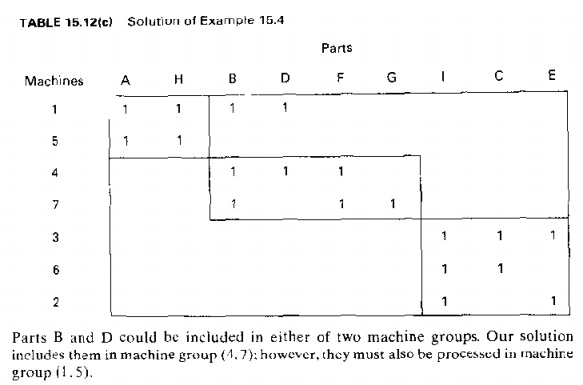
Parts B and D could be included in either of two machine groups. Our solution includes them in machine group (1.7); however, they must also be processed in machine group (1. 5)

King [26] refers  to the matrix  elements  Bl and Dj  (parts  Band  D processed  on machine    in Table 15.l2(c)  as exceptional   elements,  He recommends   that they each he replaced with an asterisk  (*) and  treated  as zeros  when applying  the rank order  clustering technique.  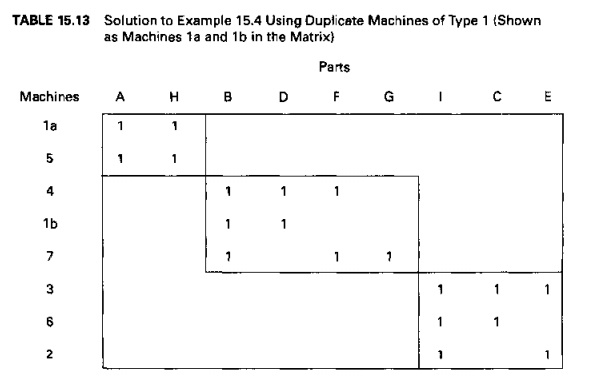The effect  of' this approach  in our example  problem  would  be to organize  the machines exactly as we have done in our final solution in Table 15.12(c).Another way of dealing with the overlap h simply to duplicate the machine that is used by more than one part family. In Example 15.4, this would mean that two machines of type 1 would be used in the two censTbe result of this duplication is shown in the matrix of Table 15.13.where the two machines are identified as l a and j b. Of course. there may be economic considerations that would inhibit the machine redundancy.

Other approaches to the problem of overlapping machines, attributed to Burbidge [26J, include: (1) change the routing so that all processing can be accomplished in the pn. mary machine group. (2) redesign the part to eliminate the processing requirement outside the primary machine group, and (3) purchase the part from an outside supplier.

            Arranging  Machines  in 8 GT Cell

After part-machine groupings have been identified by rank order clustering or other method. the next problem is to organize the machines into the most logical arrangement. Let us describe two simple yet effective methods suggested by Hollier [17]. Both methods use data contained in From-To charts (Section 10.6.1) and are intended to arrange the machines in an order that maximizes the proportion of in-sequence moves within the cell

Hollier Method 1. The first method uses the sums of flow "From" and "To" each machine in the cell. The method can be outlined as follows:

Develop the From-To chart from part routing data. The data contained in the chart indicates numbers of part moves between the machines (or workstations) in the cell. Moves into and out of the cell are not included in the chart.

    Determine the “From”  and “TO” sums for each machine. This is accomplished by summing all of the "From" trips and "To" trips for each machine (or operation). The "From" sum for a machine is determined by adding the entries in the corresponding row, and the "To" sum is found by adding the entries in the corresponding column.

    Assign machines to the cell hosed on minimum "From" or "To" sums. The machine having the smallest sum is selected. If the minimum value is a "To" sum, then the machine is placed at the beginning of the sequence. If the minimum value is a "From" sum, then the machine is placed at the end of the sequence. TIe breaker rules:

     If a tie occurs between minimum "To" sums or minimum "From" sums, then the machine with the minimum "From/To" ratio is selected.

     If both "To" and "From" sums are equal for a selected machine,it is passed over and the machine with the next lowest sum is selected.

     If a minimum "To" sum is equal to a minimum "From" sum, then both machines are selected and placed at the beginning and end of the sequence, respectively.

Reformat the From-To chan. After each machine has been selected, restructure the From-To chart by eliminating the row and column corresponding to  the selected machine and recalculate the "From" and "To" sums. Repeat steps 3 and 4 until all machines have been assigned.

EXAMPLE     15.5          Group  Technology    Machine     Sequence    using Hollier  Method 1

Suppose that four machines. I, 2.3, and 4 have been identified as belonging in a GT machine cell. An analysis of 50 parts processed on these machines has been summarized in the From-To chart of Table 15.14. Additional information is that '50 parts enter the machine grouping at machine 3,20 parts leave after processing at machine 1, and 30 parts leave after machine 4. Determine a logical machine arrangement using Hollier Method 1.

Solution: Summing the From trips and To trips for each machine yields the "From" and "To" sums in Table 15.15(a). The minimum sum value is the "To" sum for machine 3. Machine 3 is therefore placed at the beginning of the sequence. Eliminating the row and column corresponding to machine 3 yields the revised From-To chart in Table 15.15(b). The minimum sum in this chart is the "To"

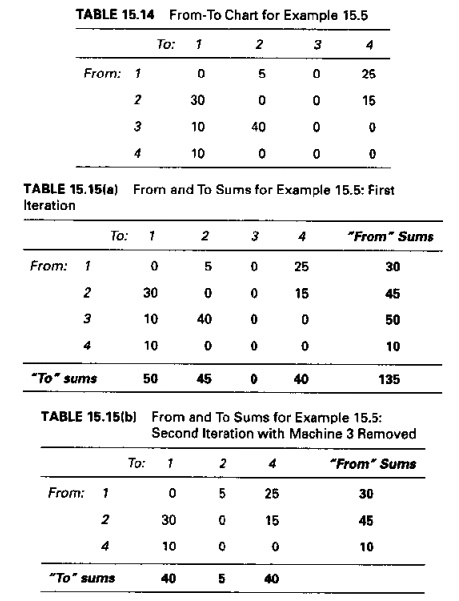
sum corresponding to machine 2. which is placed at the front at the sequence, immediately following machine 3. Eliminating machine 2 produces the revised From-To chart in Table 15.15(c). The minimum sum in this chart is the "To" sum for machine I. Machine I is placed after machine 2 and finally machine 4 is placed at the end of the sequence. Thus, the resulting machine sequence is

3-- > 2 -- > 1 -- > 4

Hollier Method 2. This approach is based on the use of From/To ratios formed by summing the total flow from and to each machine in the cell. The method can he reduced to three steps:

   Develop  the From-To  chart. This is the same step as in Hollier  Method  1.

    Determine the From/To ratio for each machine. This i~ accomplished by summing up all of the "From" trips and "To" trips for each machine (or operation). The "From" sum for a machine is determined by adding the entries in the corresponding row, and the "To" sum is determined by adding the entries in the corresponding column. For each machine, the From/To ratio is calculated by taking the "From" sum for each machine and dividing by the respective "To" sum.

    Arrange machines in order of decreasing From/To ratio. Machines with II high From/To ratio distribute work to many machines in the cell but receive work from few machines. Conversely, machines with a low From/To ratio receive more work than they distribute. Therefore, machines are arranged in order of descending Prom/Io ratio. That is, machines with high ratios are placed at the beginning of the work flow, and machine, with low ratios are placed at the end of the work flow. in case of a tie, the machine with the higher "From" value is placed ahead of the machine with a lower value

EXAMPLE     15.6 Group Technology Machine Sequence using  Hollier Method 2

Solve Example   15.5 using Hollier   Method       2.

Solution: Table 15.15(a), containing the "From" and "To" sums, is repeated in Table 15.16, along with the From/To ratios given in the last column on the right. Arranging the machines III order of descending Prom/To ratio, the machines in the cell should he sequenced as follows'

3 -- > 2 -- > 1 -- > 4

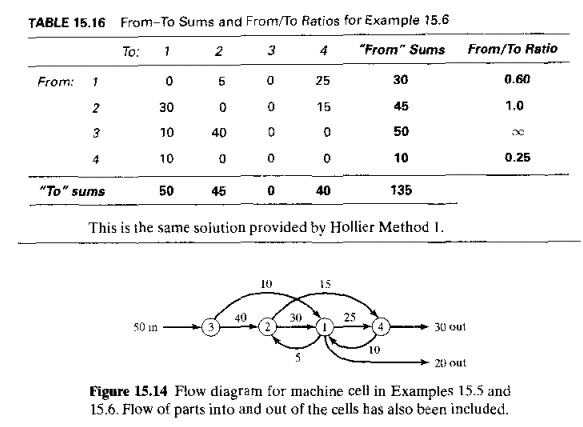
It is helpful to use one of the available graphical techniques, such as the flow diagram (Section 10.6.1), to conceptualize the work flow in the cell. The flow diagram for the machine arrangement in Examples 15.5 and 15.6 is presented in Figure 15,14. The work flow is mostly inline; however, there is some back flow or parts that must be considered in the design of any material handling system that might be used in the cell. A powered convey or would be appropriate for the forward flow between  machines. with manual handling for the back flow.

For our example data in Table 1'1.14, Hollier Methods 1 and 2 provide the same solution. This is not always the case. The relative performance of the two methods depends on the given problem. In some problems. Method J will outperform Method 2.and in other problems the opposite will happen. In many problems, the two methods yield identical solutions, as in Examples 15.5 and 15.0. Hollier presents a comparison of these and his other proposed methods with a variety of problems in [17].

Two performance       measures    can be defined to compare solutions     to the machine sequencing problem: (1) percentage of in-sequence moves and (2) percentage of backtracking moves. The percentage of in-sequence moves is computed by adding all of the values representing in-sequence moves and dividing by the total number of moves. The percentage of backtracking moves is determined by summing all of the values representing backtracking moves and dividing by the total number of moves.

EXAMPLE       15.7      Performance       Measures    for Alternative     Machine     Sequence ••in GT cell

Compute (a) the percentage of in-sequence moves and (b) the percentage of backtracking moves for the solution in Examples 15.5 and 15.6.