Prestressed Concrete Structures: Analysis of beam section- concept

Analysis of beam section - concept

Sign convention

1.     Tension is (+)

2.      Compression is (-)

Different concepts

Different concepts can be applied to the analysis if PSC concrete beams, namely

1.     Pre-stressing transforms concrete into an elastic material.

2. Pre-stressing is a combination of high-strength steel and concrete.

3. Pre-stress balances loads.

Elastic material

This concept treats concrete as an elastic material and is the most common among engineers. Here concrete is visualized as being subjected to:

1.     Internal pre-stress

2.     External loads.

So long as there are no cracks in the section, the stresses, strains and deflections of the concrete due to the two systems of forces can be considered separately and superimposed if needed.

Due to a tensile pre-stressing force F, thee resulting stress at a section is given below.

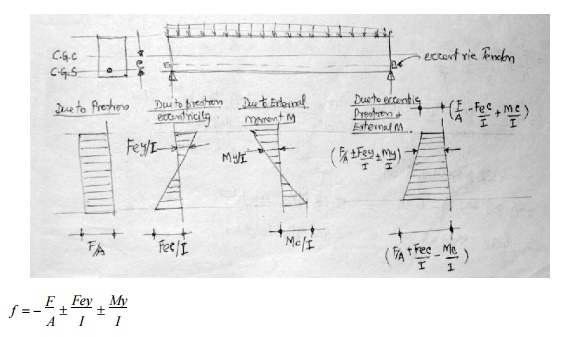
The concrete stress at a section due to pre-stress f is dependant only on the magnitude and location of pre-stress at that section, ie., F and e, regardless of how the tendon profile varies elsewhere along the beam.

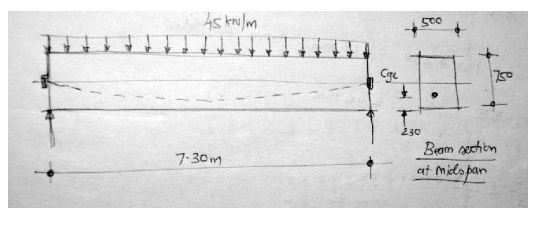
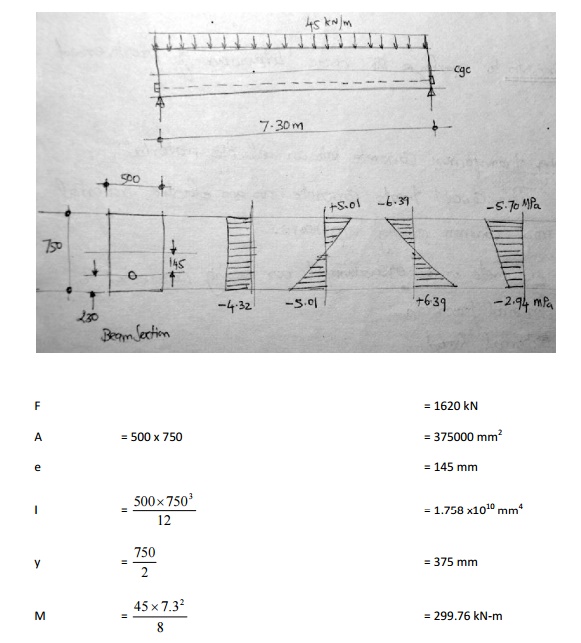
Ex 1

A pre-stress concrete rectangular beam of size 500 mm x 750 mm has a simple span of 7.3 m and is loaded with a udl of 45 kN/m including its self-weight. An effective pre-stress of 1620 kN is produced. Compute the fiber stresses in concrete at mid-span section.

High strength steel and concrete

This considers the pre-stressed concrete as combination of steel and concrete similar to RCC. Tension exists in steel and compression in concrete. These two form a internal resisting couple against external moment produced by loads.

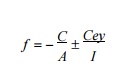
[Note: Stresses are calculated with force and eccentricity in concrete. e is the eccentricity of C, the compressive force in concrete.]

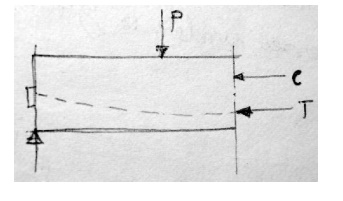
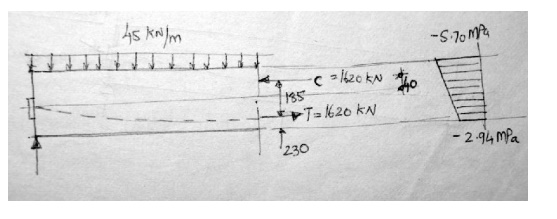
Ex 2

Solve Ex.1 using this concept.

Load balancing

The effect of pre-stressing is considered as the balancing of gravity loads so that the member under bending will not be subjected to flexural stresses under a given loading condition.

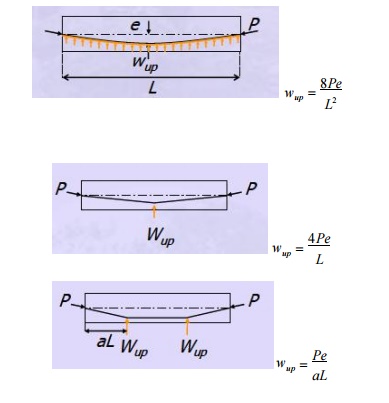
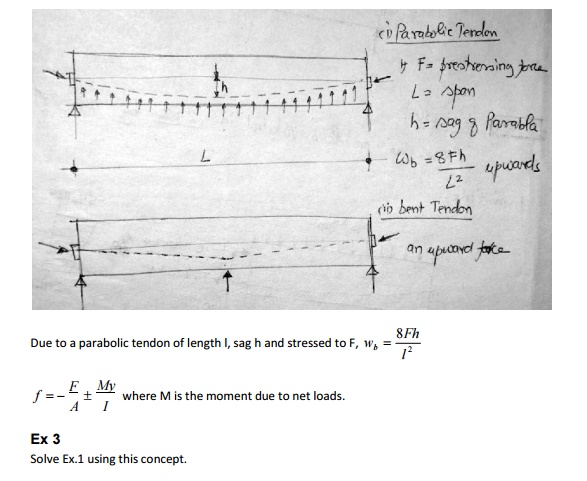
Analysis of beam section for flexure

Stress in concrete and steel due to pre-stress only

Example - Pre-tensioned member - concentric tendon

A pre-tensioned beam of size 200 mm x 300 mm is concentrically pre-stressed with 520 mm² wires anchored to bulkheads with a f_i  = 1035 MPa. Assuming n = 6, compute the stresses in concrete and steel immediately after transfer due to pre-stress only.

Example - Pre-tensioned member - eccentric tendon

A pre-tensioned beam of size 200 mm x 300 mm is eccentrically pre-stressed with 520 mm² wires anchored to bulkheads with a fi = 1035 MPa. The cgs is 100 mm above the bottom of the beam. Assuming n = 6, compute the stresses in concrete and steel immediately after transfer due to pre-stress only.

Which show that the approximate method is fast and quite accurate.

Example - Post-tensioned member - eccentric tendon

A post-tensioned beam of size 200 mm x 300 mm is eccentrically pre-stressed with 520 mm² wires stressed to a f_i = 1035 MPa. The cgs is 75 mm above the bottom of the beam. Immediately after transfer the stress reduces by 5% owing to anchorage and other losses. The size of the duct is 50 mm x 75 mm. Compute the stresses in concrete and steel immediately after transfer due to pre-stress only.

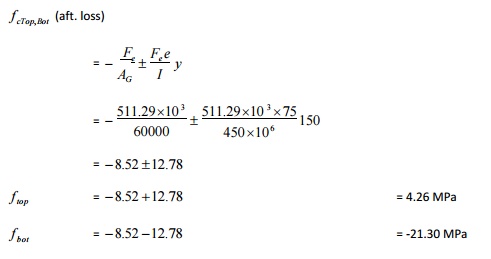
Stress in concrete due to pre-stress & loads

Stresses in concrete produced by external bending moment, whether due to the beam's self-weight or applied load is:

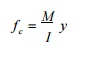
The resulting stress in concrete due to both the pre-stress and loads is:

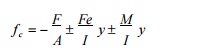
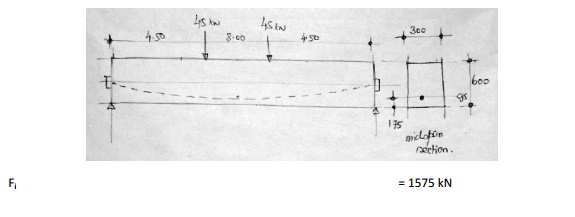
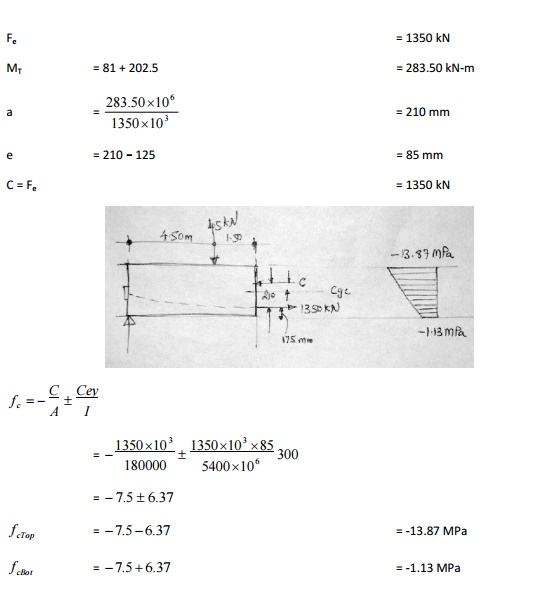
Example - Post-tensioned member with loads

A post-tensioned beam of size 300 mm x 600 mm and le = 12 m is pre-stressed with1575 kN which eventually reduces to 1350 kN due to losses. The cgs is 175 mm above the bottom of the beam. The beam carries two live loads of 45 kN each in addition to its self-weight of 4.5 kN/m. Compute the extreme fiber stresses at mid-span for (a) initial condition with full pre-stress and no live load and (b) pre-stress after losses with full live load.

Example - Post-tensioned member with loads

Solve Ex  by locating the center of pressure C for concrete section.

Stress in steel due to loads

In RCC members, the lever arm between the resultant compression and tension remains almost constant but the tension in steel increases almost proportionately with increasing moment till yielding.

In pre-stress concrete resistance to external bending moments is furnished by a lengthening of the lever arm between the resisting forces C and T which remain relatively unchanged in magnitude.

After cracking, the stress in pre-stressing steel increases rapidly with moment.

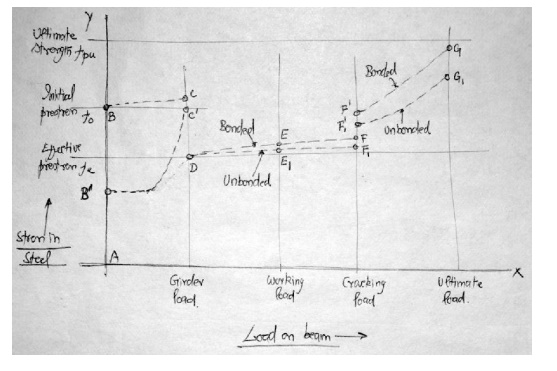
The following sketch explains the variations of the stress in pre-stressing steel f _p with increasing load.

The variations are shown for bonded and un bonded tendons.

After the pre-stress is transferred while the member is supported at the ends, the stress will tend to increase from the value after losses f _po due to the moment under self weight. Simultaneously the stress will tend to drop due to the time dependent losses such as creep, shrinkage and relaxation. The effective pre-stress after time dependent losses is denoted as f _pe

Due to the moment under service loads, the stress in the pre-stressing steel will slightly increase from f_pv . The increase is more at the section of maximum moment in a bonded tendon as compared to the increase in average stress for an un bonded tendon.

The stress in a bonded tendon is not uniform along the length. Usually the increase in stress is neglected in the calculations under service loads. If the loads are further increased, the stress increases slightly till cracking.

After cracking, there is a jump of the stress in the pre-stressing steel. Beyond that, the stress increases rapidly with moment till the ultimate load. At ultimate, the stress is f _pu .

Similar to the observation for pre-cracking, the average stress in an un bonded tendon is less than the stress at the section of maximum moment for a bonded tendon.

As discussed above, at the section of maximum moment, the stresses in the un bonded tendon increases more slowly than that for bonded tendon. This is because any strain in an un bonded tendon will be distributed throughout its entire length.

If MR is the resultant moment in at a cross-section of a bonded beam and the beam deflects downwards, there is an increase in steel stress due to this bending given by

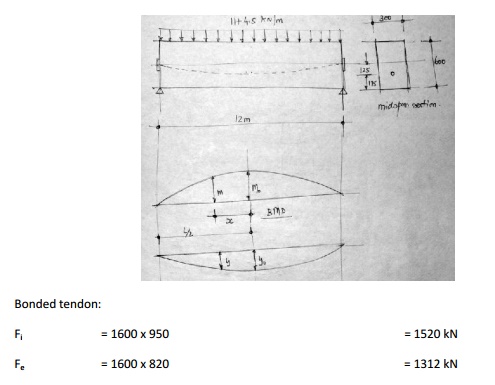
Example - stress in steel

A post-tensioned beam of span le = 12 m and size 300 mm x 600 mm, carries a superimposed load of 11 kN/m in addition to its own weight of 4.5 kN/m. The initial pre-stress in steel is 950 MPa and reduces to 820 MPa after all losses and assuming no bending in beam. The cable of are 1600 mm² is parabolic. N=6. Compute the stress in steel at mid-span assuming (a) the steel is bonded by grouting and (b) the steel is un bonded and entirely free to slip.

Cracking moment

Moments producing first crack in a pre-stressed concrete beam, assuming cracks start when tensile stress in the extreme fiber of concrete reaches its modulus of rupture, f_cr ,

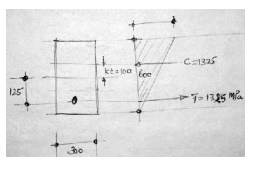
Example

For the problem in 6.3.1 compute the total dead and live load that can be carried by the beam for (a) zero tensile stress at bottom fiber and (2) cracking in the bottom fiber assuming f _cr= 4.2MPa and Fe = 

1350 kN.