Chapter: An Introduction to Parallel Programming : Distributed-Memory Programming with MPI
Performance Evaluation of MPI Programs
PERFORMANCE EVALUATION OF MPI PROGRAMS
Let’s take a look at the
performance of the matrix-vector multiplication program. For the most part we
write parallel programs because we expect that they’ll be faster than a serial
program that solves the same problem. How can we verify this? We spent some
time discussing this in Section 2.6, so we’ll start by recalling some of the
material we learned there.
1. Taking timings
We’re usually not interested in the time taken
from the start of program execution to the end of program execution. For
example, in the matrix-vector multiplication, we’re not interested in the time
it takes to type in the matrix or print out the product.
Program 3.13: The Get
input function with a derived datatype
void Build_mpi_type(
double* a_p /* in */,
double* b_p /* in */,
int* n_p /* in */,
MPI_Datatype* input
mpi t p /* out */)
{
int array_of_blocklengths[3] = {1, 1, 1};
MPI_Datatype_array_of_types[3] = { MPI_DOUBLE, MPI_DOUBLE, MPI_INT};
MPI_Aint a_addr, b_addr, n_addr;
MPI_Aint array_of_displacements[3] = {0};
MPI_Get_address(a_p, &a addr);
MPI_Get_address(b_p, &b_addr);
MPI_Get_address(n_p,
&n_addr);
array of displacements[1] = b_addr - a_addr;
array_of_displacements[2] = n_addr - a_addr;
MPI_Type_create struct(3, array_of_blocklengths,
array_of_displacements, array_of_types,
input_mpi_t_p);
MPI_Type_commit(input_mpi_t_p);
/* Build mpi type */
void Get_input(int my_rank, int comm_sz, double
a_p, double b_p, int n_p) {
MPI_Datatype input_mpi_t;
Build_mpi_type(a_p, b_p, n_p, &input_mpi_t);
if (my_rank == 0) {
printf("Enter a, b, and n\n");
scanf("%lf %lf %d", a_p, b_p, n_p);
}
MPI_Bcast(a_p, 1, input_mpi_t, 0, MPI_COMM_WORLD);
MPI_Type_free(&input_mpi_t);
/* Get input
*/
We’re only interested in the time it takes to
do the actual multiplication, so we need to modify our source code by adding in
calls to a function that will tell us the amount of time that elapses from the
beginning to the end of the actual matrix-vector mul-tiplication. MPI provides
a function, MPI Wtime, that returns the number of seconds that have elapsed since some
time in the past:
double MPI_Wtime(void);
Thus, we can time a block of MPI code as
follows:
double start, finish;
start = MPI_Wtime();
/* Code to be timed */
. . .
finish = MPI_Wtime();
printf("Proc %d > Elapsed time = %e
secondsnn" my_rank, finish-start);
In order to time serial code, it’s not
necessary to link in the MPI libraries. There is a POSIX library function
called gettimeofday that returns the number of microsec-onds that have elapsed since
some point in the past. The syntax details aren’t too important. There’s a C
macro GET TIME defined in the header file timer.h that can be downloaded from the book’s
website. This macro should be called with a double argument:
#include "timer.h"
. . .
double now;
. . .
GET_TIME(now);
After executing this macro, now will store the number of seconds since some time in the past. We
can get the elapsed time of serial code with microsecond resolution by
executing
#include "timer.h"
. . .
double start, finish;
. . .
GET_TIME(start);
/* Code to be timed */
. . .
GET_TIME(finish);
printf("Elapsed time = %e secondsnn",
finish-start);
One point to stress here: GET TIME is a macro, so the code that defines it is inserted directly into
your source code by the preprocessor. Hence, it can operate directly on its
argument, and the argument is a double, not a pointer to a double. A final note in this connection: Since timer.h is not in the system include file directory, it’s necessary to
tell the compiler where to find it if it’s not in the directory where you’re
compiling. For example, if it’s in the directory /home/peter/my
include, the following command can be used to compile
a serial program that uses GET TIME:
$ gcc -g -Wall -I/home/peter/my_include -o
<executable>
<source code.c>
Both MPI
Wtime and GET TIME return wall clock time. Recall that a timer like the C clock function returns CPU time—the time spent in user code, library
functions, and operating system code. It doesn’t include idle time, which can
be a significant part of parallel run time. For example, a call to MPI Recv may spend a significant amount of time waiting for the arrival of
a message. Wall clock time, on the other hand, gives total elapsed time, so it
includes idle time.
There are still a few remaining issues. First,
as we’ve described it, our parallel program will report comm sz times, one for each process. We would like to have it report a
single time. Ideally, all of the processes would start execution of the
matrix-vector multiplication at the same time, and then, we would report the
time that elapsed when the last process finished. In other words, the parallel
execution time would be the time it took the “slowest” process to finish. We
can’t get exactly this time because we can’t insure that all the processes
start at the same instant. However, we can come reasonably close. The MPI
collective communication function MPI
Barrier insures that no process will return from
calling it until every process in the communicator has started calling it. It’s
syntax is
int MPI_Barrier(MPI_Comm comm /* in */);
The following code can be used to time a block
of MPI code and report a single elapsed time:
double local_start, local_finish, local_elapsed,
elapsed;
MPI_Barrier(comm);
local_start = MPI_Wtime();
/* Code to be timed */
. . .
local_finish = MPI_Wtime();
local elapsed = local finish - local_start;
MPI_Reduce(&local_elapsed, &elapsed, 1,
MPI_DOUBLE, MPI_MAX, 0, comm);
if (my_rank == 0)
printf("Elapsed time = %e secondsnn",
elapsed);
Note that the call to MPI_Reduce is using the MPI_MAX operator; it finds the largest of the input
arguments local elapsed.
As we noted in Chapter 2, we also need to be
aware of variability in timings: when we run a program several times, we’re
likely to see a substantial variation in the times. This will be true even if
for each run we use the same input, the same number of processes, and the same
system. This is because the interaction of the program with the rest of the
system, especially the operating system, is unpredictable. Since this
interaction will almost certainly not make the program run faster than it would
run on a “quiet” system, we usually report the minimum run-time rather than the mean or median. (For further discussion
of this, see [5].)
Finally, when we run an MPI program on a hybrid
system in which the nodes are multicore processors, we’ll only run one MPI
process on each node. This may reduce contention for the interconnect and
result in somewhat better run-times. It may also reduce variability in
run-times.
2. Results
The results of timing the matrix-vector
multiplication program are shown in Table 3.5. The input matrices were square.
The times shown are in milliseconds,
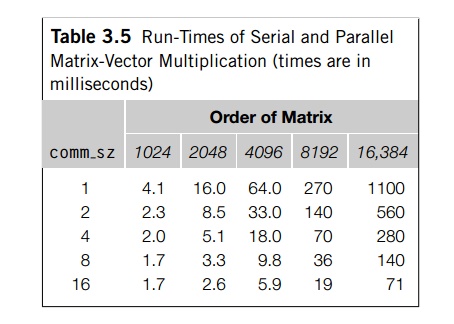
and we’ve rounded each time to two significant
digits. The times for comm_sz = 1 are the run-times of the serial program
running on a single core of the distributed-memory system. Not surprisingly, if
we fix comm_sz, and increase n, the order of the matrix, the run-times increase. For relatively
small numbers of processes, doubling n results in roughly a four-fold increase in the run-time. However,
for large numbers of processes, this formula breaks down.
If we fix n and increase comm_sz, the run-times usually decrease. In fact, for
large values of n, doubling the number of processes roughly halves the overall
run-time. However, for small n, there is very little benefit in increasing comm sz. In fact, in going from 8 to 16 processes when n = 1024, the overall run time is unchanged.
These timings are fairly typical of parallel
run-times—as we increase the problem size, the run-times increase, and this is
true regardless of the number of processes. The rate of increase can be fairly
constant (e.g., the one-process times) or it can vary wildly (e.g., the
16-process times). As we increase the number of processes, the run-times
typically decrease for a while. However, at some point, the run-times can
actually start to get worse. The closest we came to this behavior was going
from 8 to 16 processes when the matrix had order 1024.
The explanation for this is that there is a
fairly common relation between the run-times of serial programs and the
run-times of corresponding parallel programs. Recall that we denote the serial
run-time by Tserial. Since
it typically depends on the size of the input, n, we’ll frequently denote it as Tserial(n). Also recall that we denote
the parallel run-time by Tparallel. Since
it depends on both the input size, n, and the number of processes, comm_sz= p, we’ll frequently denote it as Tparallel(n, p). As we noted in Chapter 2, it’s often the case
that the parallel program will divide the work of the serial program among the
processes, and add in some overhead time, which we denoted Toverhead:
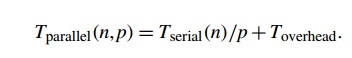
In MPI programs, the parallel overhead
typically comes from communication, and it can depend on both the problem size
and the number of processes.
It’s not too hard to see that this formula
applies to our matrix-vector multiplication program. The heart of the serial
program is the pair of nested for loops:
for (i = 0; i < m; i++)
{
y[i] = 0.0;
for (j = 0; j < n; j++)
y[i] += A[i n+j] x[j];
}
If we only count floating point operations, the
inner loop carries out n multiplications and n additions, for a total of 2n floating point operations. Since we execute the inner loop m times, the pair of loops executes a total of 2mn floating point operations. So when m D n,
Tserial(n) ~~ an2
for some constant a. (The symbol ~~ means “is approximately equal to.”)
If the serial program multiplies an nx n matrix by an n-dimensional vector, then each process in the parallel program
multiplies an n/p x n matrix by an n-dimensional vector. The local matrix-vector multiplication part of the parallel pro-gram
therefore executes n2/p floating point operations.
Thus, it appears that this local matrix-vector multiplication reduces the work per process by a
factor of p.
However, the parallel program also needs to
complete a call to MPI_Allgather before it can carry out the local matrix-vector
multiplication. In our example, it appears that
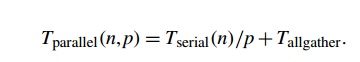
Furthermore, in light of our timing data, it
appears that for smaller values of p and larger values of n, the dominant term in our formula is Tserial(n)=p. To see this, observe first that for small p (e.g., p = 2, 4), doubling p roughly halves the overall run-time. For example,
Tserial(4096) =
1.9 x
Tparallel(4096, 2)
Tserial(8192) =
1.9 xTparallel(8192, 2)
Tparallel(8192, 2) =
2.0 x Tparallel(8192, 4)
Tserial(16, 384) =
2.0 x Tparallel(16, 384, 2)
Tparallel(16, 384, 2) =
2.0 x Tparallel(16, 384, 4)
Also, if we fix p at a small value (e.g., p = 2, 4), then increasing n seems to have approximately the same effect as increasing n for the serial program. For example,
Tserial(4096) =
4.0 Tserial(2048)
Tparallel(4096, 2) =
3.9 Tparallel(2048, 2)
Tparallel(4096, 4) =
3.5 Tparallel(2048, 4)
Tserial(8192) =
4.2x Tserial(4096)
Tparallel(8192, 2) =
4.2 xTparallel(4096, 2)
Tparallel(8192, 4) =
3.9xTparallel(8192, 4)
These observations suggest that the parallel
run-times are behaving much as the run-times of the serial program - that is, Tparallel(n, p) is approximately Tserial(n)/p - so the overhead Tallgather has
little effect on the performance.
On the other hand, for small n and large p these patterns break down. For example,
Tparallel(1024, 8) =
1.0 Tparallel(1024, 16)
Tparallel(2048, 16) =
1.5 Tparallel(1024, 16)
Thus, it appears that for small n and large p, the dominant term in our formula for
Tparallel is Tallgather.
3. Speedup and efficiency
Recall that the most widely used measure of the
relation between the serial and the parallel run-times is the speedup. It’s just the ratio of the serial run-time to
the parallel run-time:
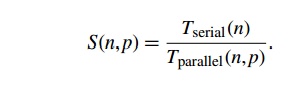
The ideal value for S(n, p) is p. If S(n, p) = p, then our parallel program with comm._sz
=
p processes is running p times faster than the serial program. In practice, this speedup, sometimes called linear speedup, is rarely achieved. Our matrix-vector
multiplication program got the speedups shown in Table 3.6. For small p and large n, our program obtained nearly linear speedup. On the other hand,
for large p and small n, the speedup was considerably less than p. The worst case was n = 1024 and p = 16, when we only managed a speedup of 2.4.


Also recall that another widely used measure of
parallel performance is parallel efficiency. This is “per process” speedup:

Linear speedup corresponds to a parallel
efficiency of p/p = 1.0, and, in general, we expect that our efficiencies will be less
than 1.
The efficiencies for the matrix-vector
multiplication program are shown in Table 3.7. Once again, for small p and large n our parallel efficiencies are near linear, and for large p and small n, they are very far from linear.
4. Scalability
Our parallel matrix-vector
multiplication program doesn’t come close to obtaining linear speedup for small
n and large p. Does this mean that it’s
not a good program? Many computer scientists answer this question by looking at
the “scalability” of the program. Recall that very roughly speaking, a program
is scalable if the problem size can be increased at a rate
so that the efficiency doesn’t decrease as the number of processes increase.
The problem with this definition
is the phrase “the problem size can be increased at a rate . . . ” Consider two
parallel programs: program A and program B. Suppose that if p>=2, the efficiency of
program A is 0.75, regardless of problem size. Also
suppose that the efficiency of program B is n/(625p), provided p>=2 and 1000<=n<=n 625p. Then according to our
“definition,” both programs are scalable. For program A, the rate of increase needed
to maintain constant efficiency is 0, while for program B if we increase n at the same rate as we
increase p, we’ll maintain a constant efficiency. For
example, if n = 1000 and p = 2, the efficiency of B is 0.80. If we then double p to 4 and we leave the
problem size at n = 1000, the efficiency will
drop to 0.40, but if we also double the problem size to n = 2000, the efficiency will remain constant at
0.80. Program A is thus more scalable than B, but both satisfy our
definition of scalability.
Looking at our table of
parallel efficiencies (Table 3.7), we see that our matrix-vector multiplication
program definitely doesn’t have the same scalability as program A: in almost every case when p
is
increased, the efficiency decreases. On the other hand, the program is somewhat
like program B: if p>=2 and we increase both p and n by a factor of 2, the parallel
efficiency, for the most part, actually increases. Furthermore, the only
exceptions occur when we increase p from 2 to 4, and when computer scientists
discuss scalability, they’re usually interested in large values of p. When p
is
increased from 4 to 8 or from 8 to 16, our efficiency always increases when we increase n by a factor of 2.
Recall that programs that can
maintain a constant efficiency without increas-ing the problem size are
sometimes said to be strongly scalable. Programs that can maintain
a constant efficiency if the problem size increases at the same rate as the
number of processes are sometimes said to be weakly scalable. Program A is strongly scalable, and
program B is weakly scalable. Furthermore, our
matrix-vector multiplication program is also apparently weakly scalable.
Related Topics