Chapter: An Introduction to Parallel Programming : Distributed-Memory Programming with MPI
A Parallel Sorting Algorithm
A PARALLEL SORTING ALGORITHM
What do we mean by a parallel
sorting algorithm in a distributed-memory envi-ronment? What would its “input”
be and what would its “output” be? The answers depend on where the keys are
stored. We can start or finish with the keys distributed among the processes or
assigned to a single process. In this section we’ll look at an algorithm that
starts and finishes with the keys distributed among the processes. In
Programming Assignment 3.8 we’ll look at an algorithm that finishes with the
keys assigned to a single process.
If we have a total of n keys and p = comm._sz processes, our algorithm will start and finish with n/p keys assigned to each process. (As usual, we’ll assume n is evenly divisible by p.) At the start, there are no restrictions on which keys are assigned to which processes. However, when the algorithm terminates, .. the keys assigned to each process should be sorted in (say) increasing order, and if 0 q < r < p, then each key assigned to process q should be less than or equal to every key assigned to process r.
So if we lined up the keys
according to process rank—keys from process 0 first, then keys from process 1,
and so on—then the keys would be sorted in increasing order. For the sake of
explicitness, we’ll assume our keys are ordinary ints.
1. Some simple serial sorting
algorithms
Before starting, let’s look at a couple of
simple serial sorting algorithms. Perhaps the best known serial sorting
algorithm is bubble sort (see Program 3.14). The array a stores the unsorted keys when the function is called, and the
sorted keys when the function returns. The number of keys in a is n. The algorithm proceeds by comparing the
elements of the list a pairwise: a[0] is compared to a[1], a[1] is compared to a[2], and so on. Whenever a pair is out of order,
the entries are swapped, so in the first pass through the outer loop, when list_length = n, the largest value in the list will be moved into a[n-1]. The next pass will ignore this last element and it will move the
next-to-the-largest element into a[n-2]. Thus, as list_length decreases, successively more elements get
assigned to their final positions in the sorted list.
Program 3.14: Serial bubble sort
void
Bubble_sort(
int a[] /* in/out */,
int n /* in */)
{
int
list_length, i, temp;
for
(list_length = n; list_length >= 2; list_length -- )
for
(i = 0; i < list_length-1; i++)
if
(a[i] > a[i+1]) {
temp
= a[i];
a[i]
= a[i+1];
a[i+1]
= temp;
}
} /* Bubble
sort */
There isn’t much point in trying to parallelize
this algorithm because of the inher-ently sequential ordering of the
comparisons. To see this, suppose that a[i-1] = 9, a[i] = 5, and a[i+1]
= 7. The algorithm will first compare 9 and 5 and
swap them, it will then compare 9 and 7 and swap them, and we’ll have the
sequence 5, 7, 9. If we try to do the comparisons out of order, that is, if we
compare the 5 and 7 first and then compare the 9 and 5, we’ll wind up with the
sequence 5, 9, 7. Therefore, the order in which the “compare-swaps” take place
is essential to the correctness of the algorithm.
A variant of bubble sort known as odd-even transposition sort has considerably more opportunities for
parallelism. The key idea is to “decouple” the compare-swaps. The algorithm
consists of a sequence of phases, of two different types. During even phases, compare-swaps are executed on the pairs
(a[0], a[1]), (a[2], a[3]), (a[4], a[5]), …….,
and during odd phases, compare-swaps are executed on the pairs
(a[1], a[2]), (a[3], a[4]), (a[5], a[6]), ……….
Here’s a small example:
Start: 5, 9, 4, 3
Even phase: Compare-swap (5, 9) and (4, 3), getting the list 5, 9, 3, 4.
Odd phase: Compare-swap (9, 3), getting the list 5, 3, 9, 4.
Even phase: Compare-swap (5, 3) and (9, 4), getting the list 3, 5, 4, 9.
Odd phase: Compare-swap (5, 4), getting the list 3, 4, 5, 9.
This example required four phases to sort a
four-element list. In general, it may require fewer phases, but the following
theorem guarantees that we can sort a list of n elements in at most n phases:
Theorem. Suppose A is a list with n
keys, and A is the input to the odd-even transposition sort algorithm. Then, after n
phases A will be sorted.
Program 3.15 shows code for a serial odd-even
transposition sort function.
Program 3.15: Serial odd-even transposition sort
void
Odd_even_sort(
int a[] /* in/out */, {
int n /* in */)
int
phase, i, temp;
for
(phase = 0; phase < n; phase++)
if
(phase % 2 == 0) { /* Even phase */
for
(i = 1; i < n; i += 2)
if
(a[i 1] > a[i]) {
temp
= a[i];
a[i]
= a[i-1];
a[i-1] = temp;
}
}
else { /* Odd phase */
for
(i = 1; i < n-1; i += 2)
if
(a[i] > a[i+1]) {
temp
= a[i];
a[i]
= a[i+1];
a[i+1] = temp;
}
}
} /* Odd
even sort */
2. Parallel odd-even transposition
sort
It should be clear that odd-even transposition
sort has considerably more opportu-nities for parallelism than bubble sort,
because all of the compare-swaps in a single phase can happen simultaneously.
Let’s try to exploit this.
There are a number of possible ways to apply
Foster’s methodology. Here’s one:
.. Tasks: Determine the value of a[i] at the end of phase j.
Communications: The task that’s determining the value of a[i] needs to commu-nicate with either the task
determining the value of a[i-1] or a[i+1]. Also the value of a[i] at the end of phase j needs to be available for determining the value of a[i] at the end of phase j + 1.
This is illustrated in Figure 3.12, where we’ve
labeled the tasks determining the value of a[i] with a[i].

Now recall that when our sorting algorithm
starts and finishes execution, each process is assigned n/p keys. In this case our aggregation and mapping
are at least partially specified by the description of the problem. Let’s look
at two cases.
When n = p, Figure 3.12 makes it fairly clear how the algorithm should
proceed. Depending on the phase, process i can send its current value, a[i], either to process i-1 or process i +
1. At the same time, it should receive the
value stored on process i-1 or process i +
1, respectively, and then decide which of the
two values it should store as a[i] for the next phase.
However, it’s unlikely that we’ll actually want
to apply the algorithm when n = p, since we’re unlikely to have more than a few hundred or a few
thousand processors at our disposal, and sorting a few thousand values is
usually a fairly trivial mat-ter for a single processor. Furthermore, even if
we do have access to thousands or even millions of processors, the added cost
of sending and receiving a message for each compare-exchange will slow the
program down so much that it will be useless. Remember that the cost of
communication is usually much greater than the cost of “local” computation—for
example, a compare-swap.
How should this be modified when each process
is storing n/p > 1 elements? (Recall that we’re assuming that n is evenly divisible by p.) Let’s look at an example. Suppose we have p = 4 processes and n = 16 keys assigned, as shown in Table 3.8. In the first place, we
can apply a fast serial sorting algorithm to the keys assigned to each process.
For example, we can use the C library function qsort on each pro-cess to sort the local keys. Now
if we had one element per process, 0 and 1 would exchange elements, and 2 and 3
would exchange. So let’s try this: Let’s have 0 and 1 exchange all their elements and 2 and 3 exchange all of
theirs. Then it would seem natural for 0 to keep the four smaller elements and
1 to keep the larger. Similarly, 2 should keep the smaller and 3 the larger.
This gives us the situation shown in the third row of the the table. Once
again, looking at the one element per process case, in phase 1, processes 1 and
2 exchange their elements and processes 0 and 3 are idle. If process 1 keeps
the smaller and 2 the larger elements, we get the distribution shown in the
fourth row. Continuing this process for two more phases results in a sorted
list. That is, each process’ keys are stored in increasing order, and if q < r,
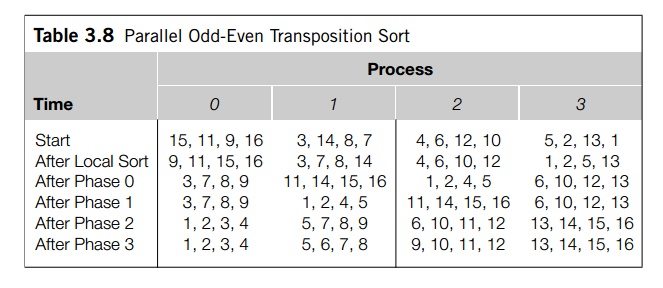
then the keys assigned to process q are less than or equal to the keys assigned to
process r.
In fact, our example illustrates the worst-case
performance of this algorithm:
Theorem. If parallel odd-even
transposition sort is run with p processes, then after p phases, the input list will
be sorted.
The parallel algorithm is clear to a human
computer:
Sort local keys;
for (phase = 0; phase < comm sz; phase++)
{ partner = Compute_partner(phase, my_rank); if
(I’m not idle) {
Send my keys to partner; Receive keys from
partner; if (my rank < partner)
Keep smaller keys;
else
Keep larger keys;
}
}
However, there are some details that we need to
clear up before we can convert the algorithm into an MPI program.
First, how do we compute the partner rank? And
what is the partner rank when a process is idle? If the phase is even, then
odd-ranked partners exchange with my rank 1
and even-ranked partners exchange with my rank+1. In odd phases, the calculations are reversed. However, these
calculations can return some invalid ranks: if my_rank = 0 or my_rank = comm_sz -1, the partner rank can be - 1 or comm_sz. But when either partner = - 1 or partner = comm._sz, the process should be idle. We can use the
rank computed by Compute_partner to determine whether a process is idle:
if (phase % 2 == 0) /* Even phase */
if (my_rank % 2
!= 0) /* Odd rank
*/
partner = my_rank 1;
else /* Even rank */
partner = my_rank
+ 1;
else / Odd phase */
if (my_rank % 2 != 0) /* Odd rank */
partner = my_rank + 1;
else /* Even rank */
partner = my_rank 1;
if (partner == - 1 || partner == comm_sz)
partner = MPI_PROC NULL;
MPI_PROC_NULL is a constant defined by MPI. When it’s used as the source or
destina-tion rank in a point-to-point communication, no communication will take
place and the call to the communication will simply return.
3. Safety in MPI programs
If a process is not idle, we might try to
implement the communication with a call to
MPI_Send and a call to MPI_Recv:
MPI_Send(my_keys, n/comm_sz, MPI_INT, partner,
0, comm);
MPI_Recv(temp_keys, n/comm_sz, MPI_INT,
partner, 0, comm,
MPI_STATUS_IGNORE);
This, however, might result in the programs’
hanging or crashing. Recall that the MPI standard allows MPI Send to behave in two different ways: it can simply copy the message
into an MPI-managed buffer and return, or it can block until the matching call
to MPI_Recv starts. Furthermore, many implementations of MPI set a threshold
at which the system switches from buffering to blocking. That is, messages that
are relatively small will be buffered by MPI_Send, but for larger messages, it will block. If
the MPI Send executed by each process blocks, no process will be able to start
executing a call to MPI_Recv, and the program will hang or deadlock, that is, each process is blocked waiting for
an event that will never happen.
A program that relies on MPI-provided buffering
is said to be unsafe. Such a program may run without problems for various sets of
input, but it may hang or crash with other sets. If we use MPI_Send and MPI Recv in this way, our program will be unsafe, and
it’s likely that for small values of n the program will run without problems, while for larger values of n, it’s likely that it will hang or crash.
There are a couple of questions that arise
here:
In
general, how can we tell if a program is safe?
How can
we modify the communication in the parallel odd-even sort program so that it is
safe?
To answer the first question, we can use an
alternative to MPI_Send defined by the MPI standard. It’s called MPI_Ssend. The extra “s” stands for synchronous and MPI_Ssend is guaranteed to block until the matching
receive starts. So, we can check whether a program is safe by replacing the
calls to MPI Send with calls to MPI_Ssend. If the program doesn’t hang or crash when
it’s run with appropriate input and comm_sz, then the original program was safe. The
arguments to MPI_Ssend are the same as the arguments to MPI_Send:
int MPI_Ssend( /* in */,
void* msg_buf_p
int msg_size /*
in */,
MPI_Datatype msg_type /*
in */,
int dest /*
in */,
int tag /*
in */,
MPI_Comm communicator /*
in */);
The answer to the second question is that the
communication must be restructured. The most common cause of an unsafe program
is multiple processes simultaneously first sending to each other and then receiving.
Our exchanges with partners is one example. Another example is a “ring pass,”
in which each process q sends to the process with rank q + 1, except that process comm._sz-1 sends to 0:
MPI_Send(msg, size, MPI_INT, (my_rank+1) %
comm_sz, 0, comm);
MPI_Recv(new msg, size, MPI_INT,
(my_rank+comm_sz-1) % comm_sz,
0, comm, MPI_STATUS_IGNORE).
In both settings, we need to restructure the
communications so that some of the pro-cesses receive before sending. For
example, the preceding communications could be restructured as follows:
if (my rank % 2 == 0) {
MPI_Send(msg, size, MPI_INT, (my_rank+1) % comm
sz, 0, comm);
MPI_Recv(new msg, size, MPI_INT, (my_rank+comm
sz 1) % comm_sz,
0, comm, MPI_STATUS_IGNORE).
} else {
MPI_Recv(new msg, size, MPI_INT,
(my_rank+comm_sz -1) % comm sz, 0, comm, MPI_STATUS_IGNORE).
MPI_Send(msg, size, MPI_INT, (my_rank+1) %
comm_sz, 0, comm);
}
It’s fairly clear that this will work if comm
sz is even. If, say, comm_sz = 4, then processes 0 and 2 will first send to 1
and 3, respectively, while processes 1 and 3 will receive from 0 and 2,
respectively. The roles are reversed for the next send-receive pairs: processes
1 and 3 will send to 2 and 0, respectively, while 2 and 0 will receive from 1
and 3.
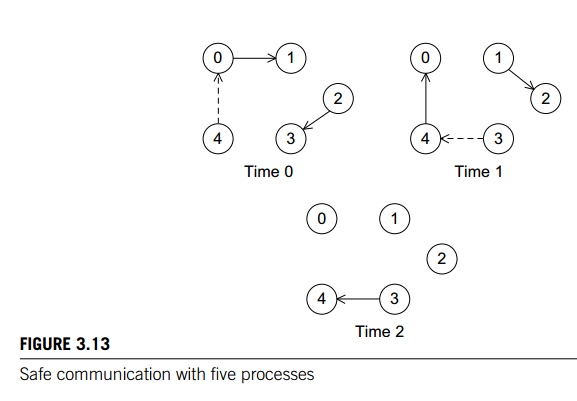
However, it may not be clear that this scheme
is also safe if comm_sz is odd (and greater than 1). Suppose, for example, that
comm_sz = 5. Then, Figure 3.13 shows a possible sequence of events. The solid
arrows show a completed communication, and the dashed arrows show a communication
waiting to complete.
MPI provides an alternative to scheduling the
communications ourselves—we can call the function MPI_Sendrecv:
int MPI_Sendrecv(
void* send_buf_p /* in */,
int send_buf_size /* in */,
MPI_Datatype send_buf_type /* in */,
int dest /* in */,
int send_tag /* in */,
Safe communication with five processes
void* recv_buf_p
int recv_buf_size
MPI_Datatype recv_buf_type
int source
int recv_tag
MPI_Comm communicator
MPI_Status status_p
This function carries out a blocking send and a
receive in a single call. The dest and the source can be the same or different.
What makes it especially useful is that the MPI implementation schedules the
communications so that the program won’t hang or crash. The complex code we
used earlier—the code that checks whether the process rank is odd or even—can
be replaced with a single call to MPI_Sendrecv. If it happens that the send and
the receive buffers should be the same, MPI provides the alternative:
int MPI_Sendrecv_replace(
void buf_p /* in/out */,
int buf_size /* in */,
MPI_Datatype buf_type /* in */,
int dest /* in */,
int send_tag /* in */,
int source /* in */,
int recv_tag /* in */,
MPI_Comm communicator /* in */,
MPI_Status status_p /* in */);
4. Final details of parallel odd-even
sort
Recall that we had developed the following
parallel odd-even transposition sort algorithm:
Sort local keys;
for (phase = 0; phase < comm._sz; phase++) {
partner = Compute_partner(phase, my_rank); if (I’m not idle) {
Send my keys to partner;
Receive keys from partner;
if (my_rank < partner)
Keep smaller keys;
else
Keep larger keys;
}
}
In light of our discussion of safety in MPI, it
probably makes sense to implement the send and the receive with a single call
to MPI Sendrecv:
MPI_Sendrecv(my_keys, n/comm_sz, MPI_INT,
partner, 0, recv_keys, n/comm_sz, MPI_INT, partner, 0, comm,
MPI_Status_ignore);
It only remains to identify which keys we keep.
Suppose for the moment that we want to keep the smaller keys. Then we want to
keep the smallest n/p keys in a collection of 2n/p keys. An obvious approach to doing this is to sort (using a serial
sorting algorithm) the list of 2n/p keys and keep the first half of the list. However, sorting is a
relatively expensive operation, and we can exploit the fact that we already
have two sorted lists of n/p keys to reduce the cost by merging the two lists into a single list. In fact, we can do even better,
because we don’t need a fully general merge: once we’ve found the smallest n/p keys, we can quit. See Program 3.16.
To get the largest n/p keys, we simply reverse the order of the merge, that is, start
with local_n- 1 and work backwards through the arrays. A final improvement avoids
copying the arrays and simply swaps pointers (see Exercise 3.28).
Run-times for the version of parallel odd-even
sort with the “final improvement” are shown in Table 3.9. Note that if parallel
odd-even sort is run on a single processor, it will use whatever serial sorting
algorithm we use to sort the local keys, so the times for a single process use
serial quicksort, not serial odd-even sort, which would be much slower. We’ll take a closer look at these times
in Exercise 3.27.

Program 3.16: The Merge
low function in parallel odd-even transposition sort
void Merge low(
int my_keys[], /* in/out */
int recv_keys[], /* in */
int temp_keys[], /* scratch */
int local_n /* = n/p, in */) {
int m_i, r_i, t_i;
m_i = r_i = t_i = 0; while (t_i < local n) {
if (my_keys[m_i] <= recv_keys[r_i]) { temp_keys[t_i]
= my_keys[m_i];
t_i++; m_i++;
} else {
temp_keys[t_i] = recv_keys[r_i]; t_i++; r_i++;
}
}
for (m_i = 0; m_i < local_n; m_i++)
my_keys[m_i] = temp_keys[m_i];
/* Merge low
*/
Related Topics