Patterns in Numbers: square, triangular numbers

Patterns in Numbers

To Identify patterns in square numbers and triangular numbers.

Square numbers

Introduction:

For finding the square of a number we multiply the number by itself. A square number is always positive. The numbers like 4, 9, 25... can be expressed as the product of a number and itself.

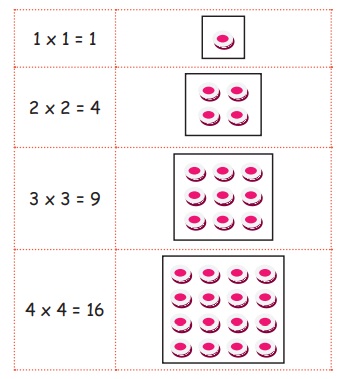
1 × 1 = 1² = 1

2 × 2 = 2² = 4

3 × 3 = 3² = 9

4 × 4 = 4² = 16 and so on..

When you multiply a number by itself, the result is a square number.

Activity

Enjoy the game Book

The teacher should say square number in order. All the students of the class should form groups according to their numbers.

Remaining students are runners up due to failure.

For example if a teacher say 4, if 33 students are in a class. All the students should create group of 8 students in the form of a square each of having 4 persons. One student will remain without a group Likewise we can play the numbers 9, 16, 25 ………

A number that can be shown using a pattern of dots in a square using flowers or small balls.

We can arrange by counting below numbers, that will make a square shape.

Think it

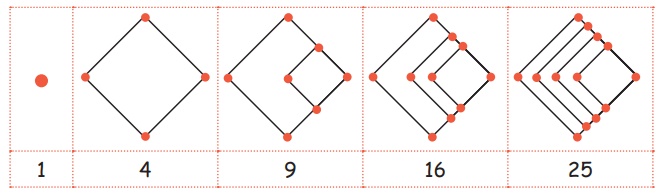
Two square numbers are added together to make another square number.

Ex. 9 + 16 = 25 Can you find other one? Answer: 100 = 36 + 64

Look at the figures shown below

Do you know

Let us know : Joshua formed a square using 12 bindis. is it 12 is a square number?

No because there are so many gapes in the square. Though the number 12 made the square. But it is not a square number.

Do yourself

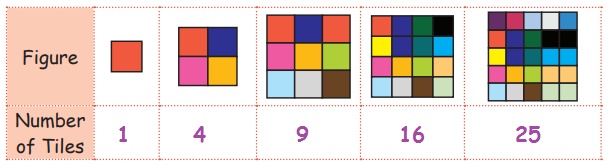
1. Count and write the tiles :

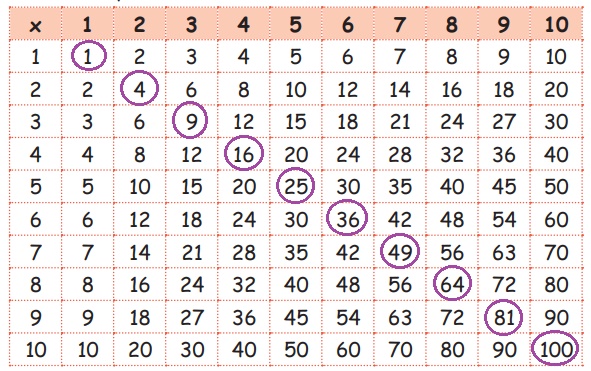
2. Circle the square numbers

Triangular Numbers

Any of the series of numbers obtained by continued summation of the natural numbers.

A number that can make a triangular dot pattern.

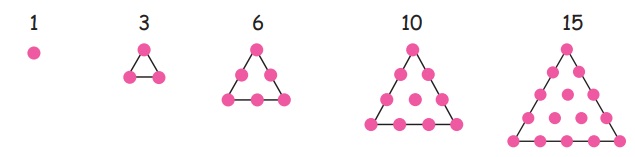
By adding another row of dots and counting all the dots we can find the next number of the sequence.

The first triangle has just 1 dot.

The second triangle has another row with 2 extra dots, making 1+2=3

The third triangle has another row with 3 extra dots, making 1+2+3=6

so, the fourth has 1+2+3+4=10. And the series goes on,

Here 1, 3, 6, 10, 15, ... are called triangular numbers.

These numbers 1, 3, 6, 10, 15, 21... etc. are in triangular shapes.

Note: Picture form of a triangular numbers can make a equilateral triangle or right angle triangle.

Do you know : What is the relationship between triangular numbers and natural numbers?

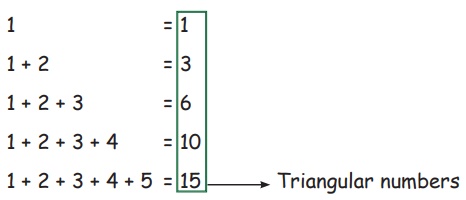
Can you understand now? Yes, The sum of consecutive natural numbers make the triangular numbers.

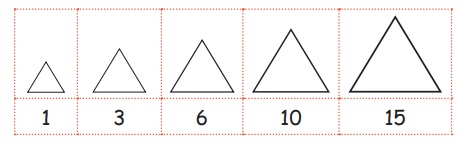
Do yourself: Make the triangle shapes in the form of series of the triangular numbers by nuts