Normal and Oblique Shocks

NORMAL AND OBLIQUE SHOCKS

Normal Shocks

When there is a relative motion between a body and fluid, the disturbance is created if the disturbance is of an infinitely small amplitude, that disturbance is transmitted through the fluid with the speed of sound. If the disturbance is finite shock waves are created.

Shock Waves and Expansion Waves Normal Shocks

Shocks which occur in a plane normal to the direction of flow are called normal shock waves. Flow process through the shock wave is highly irreversible and cannot be approximated as being isentropic. Develop relationships for flow properties before and after the shock using conservation of mass, momentum, and energy.

In some range of back pressure, the fluid that achieved a sonic velocity at the throat of a converging-diverging nozzle and is accelerating to supersonic velocities in the diverging section experiences a normal shock. The normal shock causes a sudden rise in pressure and temperature and a sudden drop in velocity to subsonic levels. Flow through the shock is highly irreversible, and thus it cannot be approximated as isentropic. The properties of an ideal gas with constant specific heats before (subscript 1) and after (subscript 2) a shock are related by

Assumptions

Ø Steady flow and one dimensional

Ø dA = 0, because shock thickness is small

Ø Negligible friction at duct walls since shock is very thin

Ø Zero body force in the flow direction

Ø Adiabatic flow (since area is small)

Ø No shaft work

Ø Potential energy neglected

Governing Equations:

(i) Continuity

 V_{x y} V_y (Shock thickness being small A_x = A_y) G_x = G_y (Mass velocity). Mass velocity remains constant across the shock.

(ii) Energy equation

To remains constant across the shock.

(iii) Momentum

Newton’s second law

Impulse function remains constant across the shock.

Property relations across the shock.

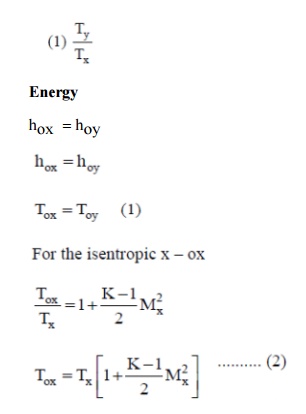
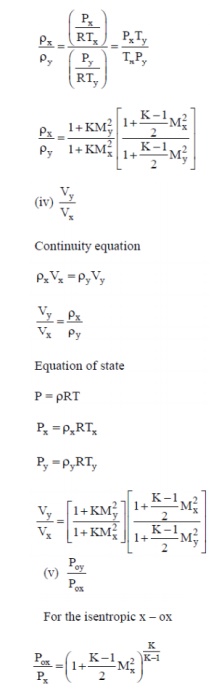
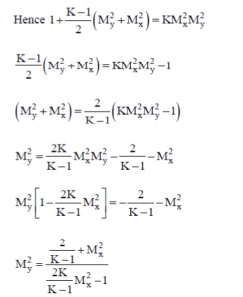
Property relations in terms of incident Mach Number M_x

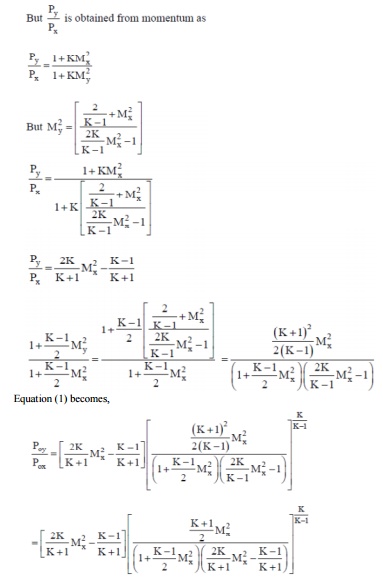
Substituting and simplifying

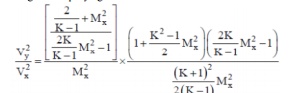
Substituting (2) in (1), we have

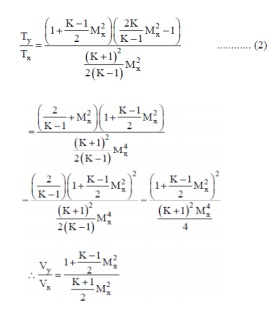
Prandtl-Meyer relationship

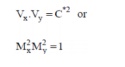
Governing relations for a normal shock

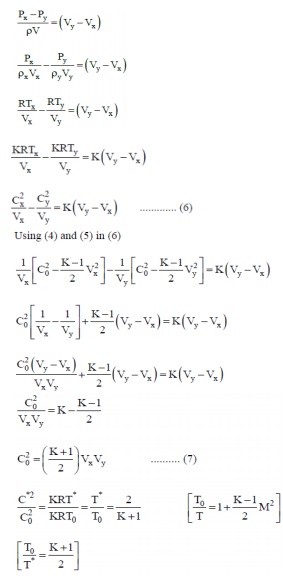
The Rankine – Hugoniot Equatios

Density Ratio Across the Shock

We know that density,

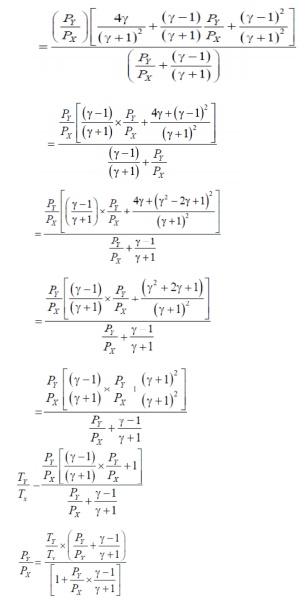
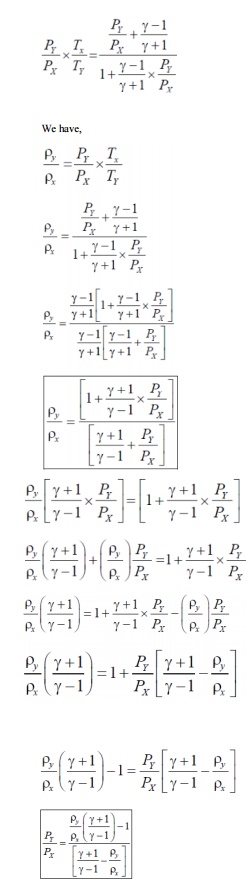
the above eqn.s is knows Rankine - Hugoniot equations.

Strength of a Shock Wave

It is defined as the ratio of difference in down stream and upstream shock pressures (p_y - p_x) to upstream shock pressures (p_x). It is denoted by ξ.

The strength of shock wave may be expressed in another form using Rankine-Hugoniot equation.

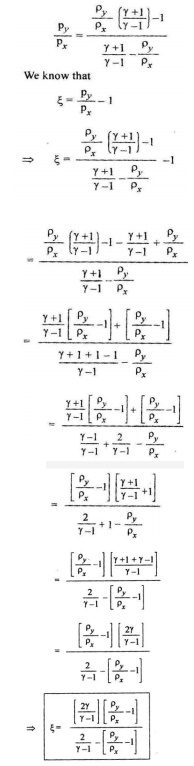
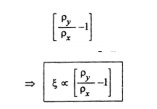
From this equation we came to know strength of shock wave is directly proportional to;

PROBLEMS

1.The state of a gas (γ=1.3,R =0.469 KJ/KgK.) upstream of normal shock wave is given by the following data: Mx =2.5, Px =2 bar. Tx =275 K calculate the Mach number,pressure,temperatureand velocity of a gas down stream of shock: check the calculated values with those given in the gas tables.Take K =γ.

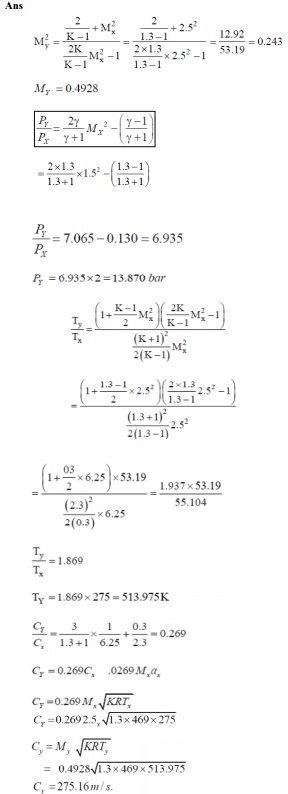
2.  An Aircraft flies at a Mach number of 1.1 at an altitude of 15,000 metres.The compression in its engine is partially achieved by a normal shock wave standing at the entry of the diffuser. Determine the following for downstream of the shock.

1. Mach number

2. Temperature of the air

3. Pressure of the air

4. Stagnation pressure loss across the shock.

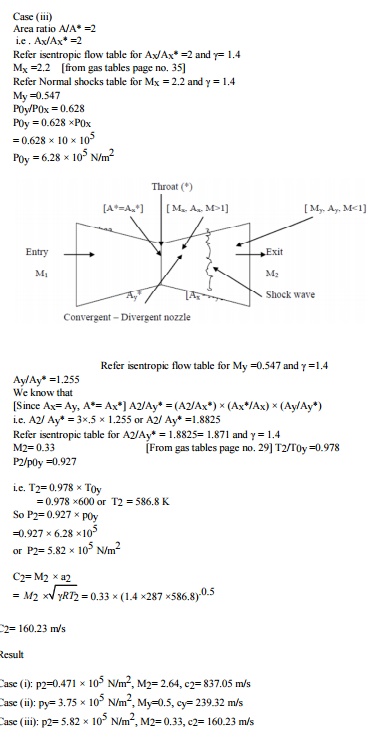
3. Supersonic nozzle is provided with a constant diameter circular duct at its exit. The duct diameter is same as the nozzle diameter. Nozzle exit cross ection is three times that of its throat. The entry conditions of the gas (γ=1.4, R= 287J/KgK) are P0 =10 bar, T0 =600K. Calculate the static pressure, Mach number and velocity of the gas in duct.

(a) When the nozzle operates at its design condition. (b) When a normal shock occurs at its exit. (c) When a normal shock occurs at a section in the diverging part where the area ratio, A/A* =2.

Given: A2 =3A*

Or A2/A*=3 γ=1.4

R= 287 J/KgK

P₀= 10 bar = 10⁶ Pa T₀= 600K

Tutorial Problems:

1) The state of a gas (γ=1.3,R =0.469 KJ/Kg K) upstream of a normal shock is given by the following data: Mx =2.5, px= 2bar ,Tx =275K calculate the Mach number, pressure,temperature and velocity of the gas downstream of the shock;check the calculated values with those give in the gas tables.

2) The ratio of th exit to entry area in a subsonic diffuser is 4.0 .The Mach number of a jet of air approaching the diffuser at p0=1.013 bar, T =290 K is 2.2 .There is a standing normal shock wave just outside the diffuser entry. The flow in the diffuser is isentropic . Determine at the exit of the diffuser.a) Mach number , b) Temperature, and c) Pressure d) What is the stagnation pressure loss between the initial and final states of the flow ?

3) The velocity of a normal shock wave moving into stagnant air (p=1.0 bar, t=17⁰C ) is 500 m/s . If the area of cross- section of the duct is constant determine (a) pressure (b) temperature

(c) velocity of air (d) stagnation temperature and (e) the mach number imparted upstream of the wave front.

4)           The following data refers to a supersonic wind tunnel:

Nozzle throat area =200cm²,Test section cross- section =337.5cm², Working fluid ;air (γ =1.4, Cp =0.287 KJ/Kg K) Determine the test section Mach number and the diffuser throat area if a normal shock is located in the test section.

5) A supersonic diffuser for air (γ =1.4) has an area ratio of 0.416 with an inlet Mach number of 2.4 (design value). Determine the exit Mach number and the design value of the pressure ratio across the diffuser for isentropic flow. At an off- design value of the inlet Mach number (2.7) a normal shock occurs inside the diffuser .Determine the upstream Mach number and area ratio at the section where the shock occurs, diffuser efficiency and the pressure ratio across the diffuser. Depict graphically the static pressure distribution at off design.

Starting from the energy equation for flow through a normal shock obtain the following relations (or) prandtl – meyer relation Cx Cy =a* ² M*x M*y =1