Measurement Scales

Measurement Scales

There are four types of data or measurements scales called nominal, ordinal, interval and ratio. These measurement scale is made by Stanley Stevens.

Nominal scales:

Nominal measurement is used to label a variable without any ordered value. For example, we can ask in a questionnaire ‘What is your gender? The answer is male or female. Here gender is a nominal variable and we associate a value 1 for male and 2 for a female.’

They are numerical for name sake only. For example, the numbers 1,2,3,4 may be used to denote a person being single, married, widowed or divorced respectively. These numbers do not share any of the properties of numbers we deal with in day to life. We cannot say 4 > 1 or 2 < 3 or 1+3 = 4 etc. The order of listings in the categories is irrelevant here. Any statistical analysis carried out with the ordering or with arithmetic operations is meaningless.

Ordinal scales:

These data share some properties of numbers of arithmetic but not all properties.

For example, we can classify the cars as small, medium and big depending on the size.

In the ordinal scales, the order of the values is important but the differences between each one is unknown. Look at the example below.

How did you feel yesterday after our trip toVedanthangal? The answers would be:

(1) Very unhappy  (2) Unhappy (3) Okay (4) Happy (5) Very happy

In each case, we know that number 5 is better than number 4 or number 3, but we don’t know how much better it is. For example, is the difference between “Okay” and “Unhappy” the same as the difference between “Very Happy” and “Happy?” In fact we cannot say anything.

Similarly,  a  medical  practitioner  can  say  the condition of a patient in the hospital as good, fair, serious and critical and assign numbers 1 for good, 2 for fair, 3 for serious and 4 for critical. The level of seriousness can be from 1 to 4 leading to 1 < 2 or 2 < 3 or 3 < 4. However, the value here just indicates the level of seriousness of the patient only.

Interval scales:

In an interval scale one can also carryout numerical differences but not the multiplication and division. In other words, an interval variable has the numerical distances between any two numbers. For example, suppose we are given the following temperature readings in Fahrenheit: 60c , 65c , 88c , 105c , 115c , and 120c. It can be written that 105c> 88cor 60c < 65c which means that 105cis warmer than 88c and that 60c is colder than 65c. It can also be written that 65c– 60c = 120c - 115c because equal temperature differences are equal conveying the same amount of heat needed to increase the temperature from an object from 60c to 65c and from 115c to 125c. However it does not mean that an object with temperature 120c is twice as hot as an object with temperature 60c, though 120c divided by 60c is 2. The reason is converting the temperature in to Celsius we have:

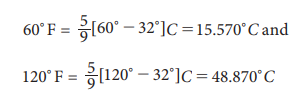
In the above equations, it is clear from the left hand side that 120cF is twice of 60cF while the right hand side says 48.87cC is more than three times of 15.57cC . The reason for the difficulty is that the Fahrenheit and Celsius scales have artificial origins namely zeros(freezing point of centigrade measure is 0^o C and the freezing point of Farenheit is 32^o F) and there is no such thing as ‘no temperature.’

Ratio scales:

Ratio scales are important when it comes to measurement scales because they tell us about the order, they tell us the exact value between units, and they also have an absolute zero–which allows for a wide range of both descriptive and inferential statistics to be applied. Good examples of ratio variables include height and weight. Ratio scales provide a wealth of possibilities when it comes to statistical analysis. These variables can be meaningfully added, subtracted, multiplied, divided). Central tendency can be measured by mean, median, or mode; Measures of dispersion, such as standard deviation and coefficient of variation can also be calculated from ratio scales.

In summary, nominal variables are used to “name,” or label a series of values. Ordinal scales provide good information about the order of choices, such as in a customer satisfaction survey. Interval scales give us the order of values plus the ability to quantify the difference between each one. Finally, Ratio scales give us the ultimate–order, interval values, plus the ability to calculate ratios since a “true zero” can be defined. The distinction made here among nominal, ordinal, interval and ratio data are very much important as these concepts used in computers for solving statistical problems using statistical packages like SPSS, SAS, R, STATA etc.,