Linear System with Random Inputs

LINEAR SYSTEM WITH RANDOM INPUTS

Introduction

Linear time invariant systems

Linear systems with random inputs

Auto Correlation and Cross Correlation functions of inputs and outputs

System transfer function

Introduction

Mathematically a "system" is a functional relationship between the input x(t) and y(t). We can write the relationship as

y(f) = f[x(t): –∞< + <∞]

Let x(t) represents a sample function of a random process {X(t)}. Suppose the system produces an output or response y(f) and the ensemble of the output functions forms a random process {Y(t)}. Then the process {Y(t)} can be considered as the output of the system or transformation 'f' with {X(t)} as the input and the system is completely specified by the operator "f".

1 LINEAR TIME INVARIANT SYSTEM

Mathematically a "system" is a functional relationship between the input x(t) and output y(t). we can write the relationship

2 CLASSIFICATION OF SYSTEM

1. Linear System: f is called a linear system, if it satisfies

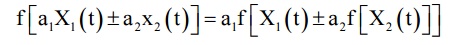
2. Time Invariant System:

form a time invariant system.

3. Causal System:

Suppose the value of the output Y(t) at t = t0 depends only on the past values of the input X(t), t≤t0.

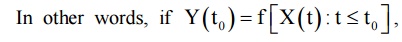
then such a system is called a causal system.

4. Memory less System:

If the output Y(t) at a given time t = t0 depends only on X(t0) and not on any other past or future values of X(t), then the system f is called memory less system.

5. Stable System:

A linear time invariant system is said to be stable if its response to any bounded input is bounded.

REMARK:

i) Noted that when we write X(t) we mean X(s,t) where s ∈ S, S is the sample space. If the system operator only on the variable t treating S as a parameter, it is called a deterministic system.

a) Shows a general single input - output linear system

b) Shows a linear time invariant system

3 REPRESENTATION OF SYSTEM IN THE FORM OF CONVOLUTION

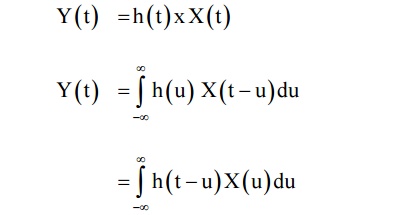
4 UNIT IMPULSE RESPONSE TO THE SYSTEM

If the input of the system is the unit impulse function, then the output or response is the system weighting function.

Y(t) = h(t)

Which is the system weight function.

4.1 PROPERTIES OF LINEAR SYSTEMS WITH RANDOM INPUT

Property 1:

If the input X(t) and its output Y(t) are related by

Property 2:

If the input to a time - invariant, stable linear system is a WSS process, then the output will also be a WSS process, i.e To show that if {X(t)} is a WSS process then the output {Y(t)} is a WSS process.

Property 3:

(ii)Equation (c) gives a relationship between the spectral densities of the input and output process in the system.

(iii)System transfer function:

We call H (ω ) = F {h (τ)} as the power transfer function or system transfer function.

SOLVED PROBLEMS ON AUTO CROSS CORRELATION FUNCTIONS OF INPUT

AND OUTPUT

Example :5.4.1

Find the power spectral density of the random telegraph signal.

Solution

We know, the auto correlation of the telegraph signal process X(y) is

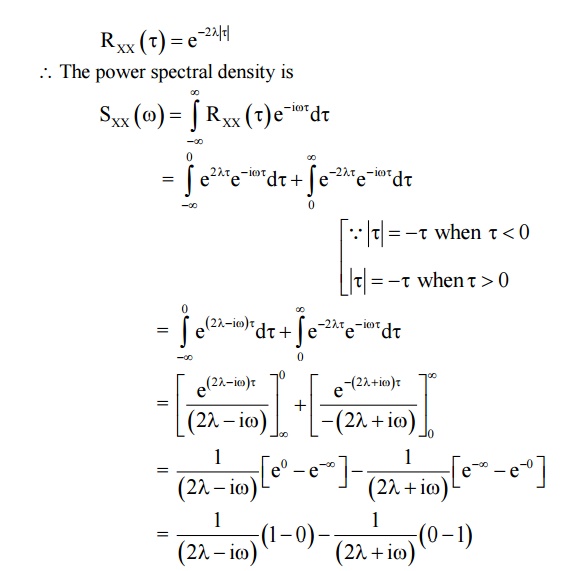
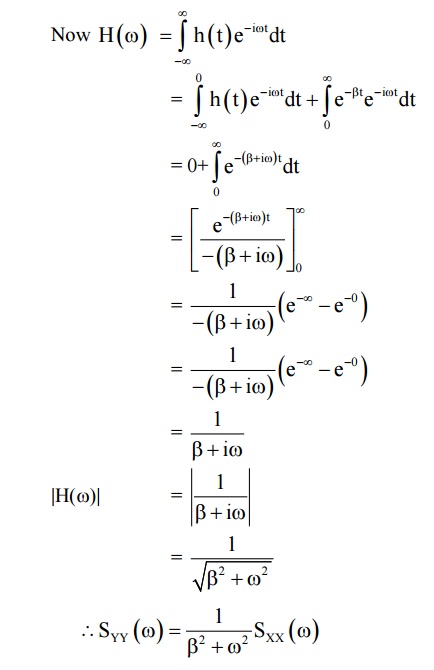
WORKEDOUT EXAMPLES

Example: 1

Find the power spectral density of the random telegraph signal.

Solution

We know, the auto correlation of the telegraph signal process X(y) is