Chapter: Signals and Systems : Analysis of Continuous Time Signals
Laplace Transform
Laplace Transform
Lapalce
transform is a generalization of the Fourier transform in the sense that it
allows ŌĆ£complex frequencyŌĆØ whereas Fourier analysis can on ly handle ŌĆ£real
frequencyŌĆØ. Like Fourier transform, Lapalce transform allows us to analyze a
ŌĆ£linear circuitŌĆØ problem, no matter how complicated the circuit is, in the
frequency domain in stead of in he time domain.
Mathematically,
it produces the benefit of converting a set of differential equations into a
corresponding set of algebraic equations, which are much easier to solve.
Physically, it produces more insight of the circuit and allows us to know the
bandwidth, phase, and transfer characteristics important for circuit analysis
and design.
Most
importantly, Laplace transform lifts the limit of Fourier analysis to allow us
to find both the steady-state and ŌĆ£transientŌĆØ responses of a linear circuit.
Using Fourier transform, one can only deal with he steady state behavior (i.e.
circuit response under indefinite sinusoidal excitation).
Using
Laplace transform, one can find the response under any types of excitation
(e.g. switching on and off at any given time(s), sinusoidal, impulse, square
wave excitations, etc.
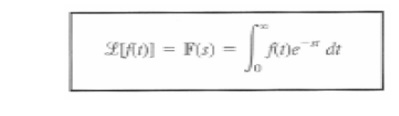

Related Topics