Distance between any Two Points

Distance between any Two Points

Akila and Shanmugam are friends living on the same street in Sathyamangalam. Shanmugam’s house is at the intersection of one street with another street on which there is a library. They both study in the same school, and that is not far from Shanmugam’s house. Try to draw a picture of their houses, library and school by yourself before looking at the map below.

Consider the school as the origin. (We can do this ! That is the whole point about the co-ordinate language we are using.)

Now fix the scale as 1 unit = 50 metres. Here are some questions for you to answer by studying the given figure (Fig 5.19).

1.        How far is Akila’s house from Shanmugam’s house ?

2.        How  far  is  the  library  from  Shanmugam’s house?

3.        How far is the school from Shanmugam’s and Akila’s house ?

4.        How far is the library from Akila’s house ?

5.        How far is Shanmugam’s house from Akila’s house ?

Question 5 is not needed after answering question 1. Obviously, the distance from point A to B is the same as the distance from point B to A, and we usually call it the distance between points A and B. But as mathematicians we are supposed to note down properties as and when we see them, so it is better to note this too: distance (A,B) = distance (B,A). This is true for all points A and B on the plane, so of course question 5 is same as question 1.

What about the other questions ? They are not the same. Since we know that the two houses are on the same street which is running north – south, the y-distance tells us the answer to question 1. Similarly, we know that the library and Shanmugam’s house are on the same street running east – west, we can take the x-distance to answer question 2.

Questions 3 and 4 depend on what kind of routes are available. If we assume that the only streets available are parallel to the x and y axes at the points marked 1, 2, 3 etc then we answer these questions by adding the x and y distances. But consider the large field east of Akila’s house.

If she can walk across the field, of course she would prefer it. Now there are many ways of going from one place to another, so when we talk of the distance between them, it is not precise. We need some way to fix what we mean. When there are many routes between A and B, we will use distance(A,B) to denote the distance on the shortest route between A and B.

Once we think of distance(A,B) as the “straight line distance” between A and B, there is an elegant way of understanding it for any points A and B on the plane. This is the important reason for using the co-ordinate system at all ! Before that, 2 more questions from our example.

1. With the school as origin, define the coordinates of the two houses, the school and the library.

2. Use the coordinates to give the distance between any one of these and another.

The “straight line distance” is usually called “as the crow flies”. This is to mean that we don’t worry about any obstacles and routes on the ground, but how we would get from A to B if we could fly. No bird ever flies on straight lines, though.

We can give a systematic answer to this: given any two points A = (x,y) and B = ( x’, y’) on the plane, find distance(A,B). It is easy to derive a formula in terms of the four numbers x, y, x’ and y’. This is what we set out to do now

1. Distance between Two Points on the Coordinate Axes

Points on x – axis: If two points lie on the x- axis, then the distance between them is equal to the difference between the x- coordinates.

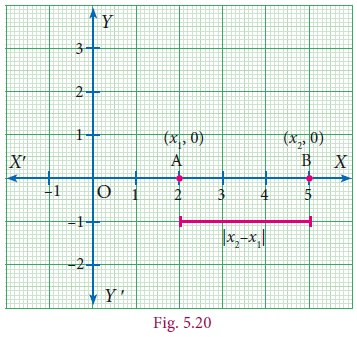
Consider two points A (x₁,0) and B (x₂,0) on the x-axis .

The distance of B from A is

AB = OB – OA = x₂- x₂ if x₂ > x₂ or

= x₂ - x₂   if x₂ >x₂

AB=|x₂-x₁|

(Read as modulus or absolute value of x₂-x₁)

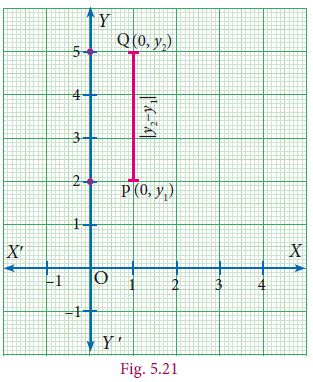
Points on x – axis: If two points lie on y-axis then the distance between them is equal to the difference between the y-coordinates.

Consider two points P(0,y₁) and Q(0,y₂)

The distance Q from P is

PQ = OQ – OP.

=  y₂-  y₂ if  y₂ >  y₂ or

=  y₂ -  y₂   if  y₂ > y₂

PQ=| y₂- y₁|

(Read as modulus or absolute value of  y₂-y₁)

2. Distance Between Two Points Lying on a Line Parallel to Coordinate Axes

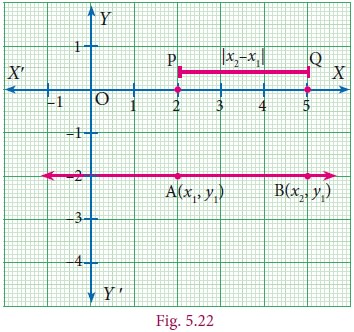
Consider the points A(x₁, y₁) and B(x₂,y₂). Since the y - coordinates are equal the points lie on a line parallel to x- axis. From A and B draw AP and BQ perpendicular to x- axis respectively. Observe the given figure (Fig. 5.22), it is obvious that the distance AB is same as the distance PQ

Distance AB = Distance between PQ = |x₂-x₁|

[The difference between x coordinates]

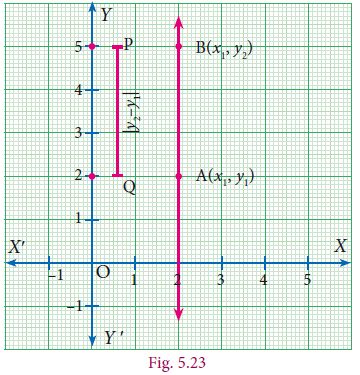
Similarly consider the line joining the two points

A(x₁,y₁) and B(x₁,y₁), parallel to y – axis.

Then the distance between these two points is

 |y₂ – y₁|

[The difference between y coordinates]

3. Distance Between the Two Points on a Plane.

Let P(x₁, y₁ ) and Q(x₂, y₂) be two points in the Cartesian plane (or xy – plane), at a distance ‘d’ apart such that d = PQ.

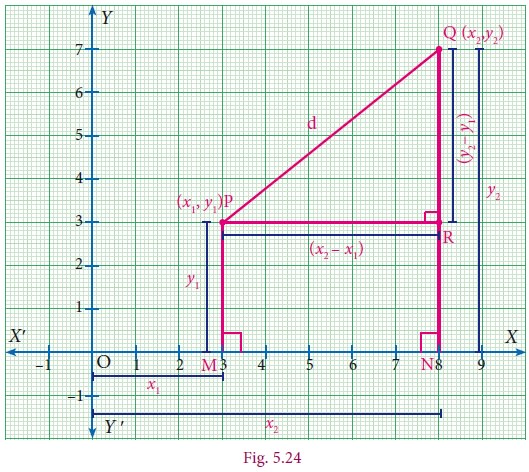
Step 1

By the definition of coordinates,

OM = x₁

MP = y₁

ON = x₂

NQ = y₂

Now PR = MN

(Opposite sides of the rectangle MNRP)

= ON – OM (Measuring the distance from O)

= x₂ – x₁ ……..(1)

And RQ = NQ – NR

= NQ – MP (Opposite sides of the rectangle MNRP)

= y₂ – y₁ ………..(2)

Step 2

Triangle PQR is right angled at R. (PR┴ NQ)

PQ² = PR² + RQ² (By Pythagoras theorem)

d² = (x₂– x₁)² + (y₂– y₁ )²

d = √{(x₂– x₁)² + (y₂– y₁ )² } (Taking positive square root)

By the definition of coordinates,

4. Properties of Distances

We have already seen that distance (A,B) = distance (B,A) for any points A, B on the plane. What other properties have you noticed ? In case you have missed them, here are some:

distance (A,B) = 0 exactly when A and B denote the identical point: A = B.

distance (A,B) >0 for any two distinct points A and B.

Now consider three points A, B and C. If we are given their co-ordinates and we find that their x-co-ordinates are the same then we know that they are collinear, and lie on a line parallel to the y-axis. Similarly, if their y-co-ordinates are the same then we know that they are collinear, and lie on a line parallel to the x-axis. But these are not the only conditions. Points (0,0), (1,1) and (2,2) are collinear as well. Can you think of what relationship should exist between these coordinates for the points to be collinear ?

The distance formula comes to our help here. We know that when A, B and C are the vertices of a triangle, we get,

distance(A,B) + distance(B,C) >distance(A,C) (after renaming the vertices suitably).

When do three points on the plane not form a triangle ? When they are collinear, of course. In fact, we can show that when,

distance(A,B) + distance(B,C) = distance(A,C), the points A, B and C must be collinear.

Similarly, when A, B and C are the vertices of a right angled triangle, +ABC = 90c we know that:

distance(AB)²+ distance(BC)² = distance(AC)²

with appropriate naming of vertices. We can also show that the converse holds: whenever the equality here holds for A, B and C, they must be the vertices of a right angled triangle.

The following examples illustrate how these properties of distances are useful for answering questions about specific geometric shapes.

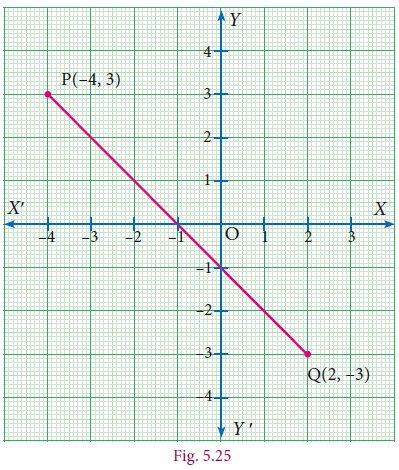
Example 5.8

Find the distance between the points (–4, 3), (2,–3).

Solution

The distance between the points (-4, 3), (2,-3) is

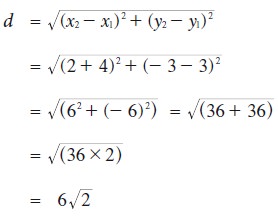
Example 5.9

Show that the following points A(3,1) , B(6,4) and C(8,6) lies on a straight line.

Solution

Example 5.10

Show that the points A(7,10), B(-2,5), C(3,-4) are the vertices of a right angled triangle.

Solution

Example 5.11

Show that the points

A(–4,–3), B(3,1), C(3,6), D(–4,2) taken in that order form the vertices of a parallelogram.

Solution

Let A(–4, –3), B(3, 1), C(3, 6), D(–4, 2) be the four vertices of any quadrilateral ABCD.

Using the distance formula,

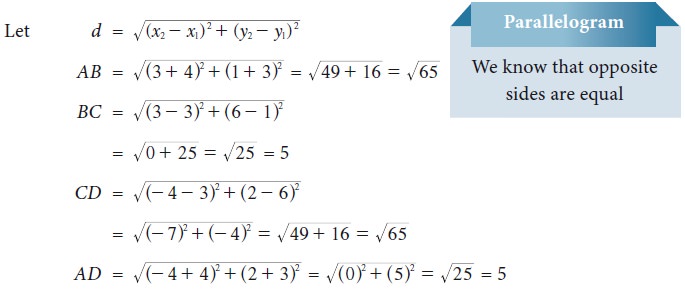
 AB = CD = √65 and BC = AD = 5

Here, the opposite sides are equal. Hence ABCD is a parallelogram.

Example 5.12

Prove that the points A(3, 5), B(6, 2), C(3,-1), and D(0, 2) taken in order are the vertices of a square.

Solution

Let A(3,5), B(6,2), C(3,-1), and D(0,2) be the vertices of any quadrilateral ABCD.

From the above results, we see that AB=BC=CD=DA= 3√2

(i.e.) All the four sides are equal.

Further, A(3, 5), C(3, –1)

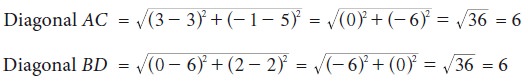
From the above we see that AB = CD = 6

Hence ABCD is a square.

Example 5.13

If the distance between the points (5,–2), (1, a), is 5 units, find the values of a.

Solution

Example 5.14

Calculate the distance between the points A (7, 3) and B which lies on the x-axis whose abscissa is 11.

Solution

Since B is on the x-axis, the y-coordinate of B is 0.

So, the coordinates of the point B is (11, 0)

By the distance formula the distance between the points A (7, 3), B (11, 0) is

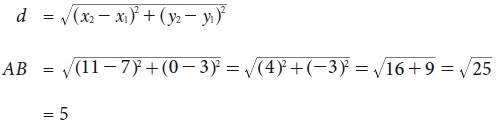
Example 5.15

Find the value of ‘a’ such that PQ = QR where P, Q, and R are the points whose coordinates are (6, –1), (1, 3) and (a, 8) respectively.

Solution

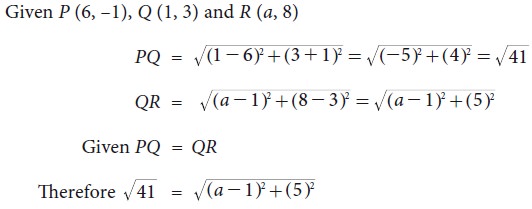
41 = (a –1)² + 25 [Squaring both sides]

 (a–1)² + 25 = 41

 (a–1)² = 41 - 25

 (a–1)² = 16

 (a–1) = ± 4 [taking square root on both sides]

 a = 1 ± 4

 a = 1 + 4 or a = 1 – 4

 a = 5, –3

Example 5.16

Let A(2, 2), B(8, –4) be two given points in a plane. If a point P lies on the X- axis (in positive side), and divides AB in the ratio 1: 2, then find the coordinates of P.

Solution

Given points are A(2, 2) and B(8, –4) and let P = (x, 0) [P lies on x axis]

By the distance formula

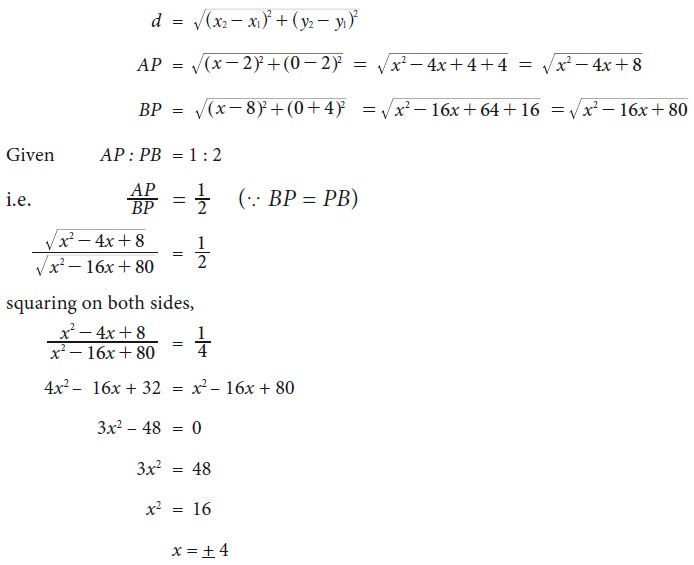
As the point P lies on x-axis (positive side), its x- coordinate cannot be –4.

Hence the coordinates of P is(4, 0)

Example 5.17

Show that (4, 3) is the centre of the circle passing through the points (9, 3), (7,–1), (–1,3).

Find the radius.

Solution

Let P(4, 3), A(9, 3), B(7, –1) and C(–1, 3)

If P is the centre of the circle which passes through the points A, B, and C, then P is equidistant from A, B and C (i.e.) PA = PB = PC

By distance formula,

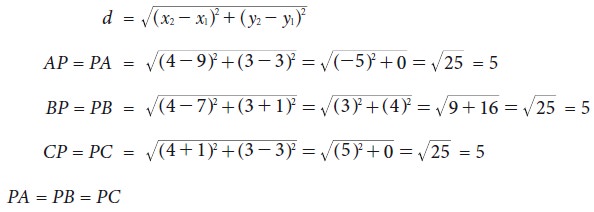
 PA = PB = PC

Therefore P is the centre of the circle, passing through A, B and C

Radius = PA = 5.