Carnot engine - Essential parts, Working, four stages of operations

Carnot engine

Heat engine is a device which converts heat energy into mechanical energy.

In the year 1824, Carnot devised an ideal cycle of operation for a heat engine. The machine used for realising this ideal cycle of

operation is called an ideal heat engine or carnot heat engine.

The essential parts of a Carnot engine are shown in Fig..

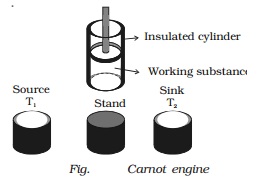
(i) Source

It is a hot body which is kept at a constant temperature T1. It has infinite thermal capacity. Any amount of heat can be drawn from it at a constant temperature T1 (i.e) its temperature will remain the same even after drawing any amount of heat from it.

(ii) Sink

It is a cold body which is kept at a constant lower temperature T₂. Its thermal capacity is also infinite that any amount of heat added to it will not increase its temperature.

(iii) Cylinder

Cylinder is made up of non-conducting walls and conducting bottom. A perfect gas is used as a working substance. The cylinder is fitted with a perfectly non-conducting and frcitionless piston.

(iv) Insulating stand

It is made up of non conducting material so as to perform adiabatic operations.

Working : The Carnot engine has the following four stages of operations.

1. Isothermal expansion 2. Adiabatic expansion 3. Isothermal compression 4. Adiabatic compression.

Isothermal expansion

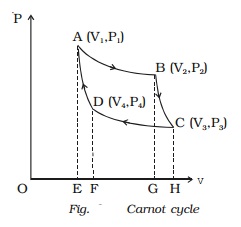
Let us consider one mole of an ideal gas enclosed in the cylinder. Let V₁, P₁ be the initial volume and pressure of the gas respectively. The initial state of the gas is represented by the point A on the P?V diagram. The cylinder is placed over the source which is at the temperature T₁.

The piston is allowed to move slowly outwards, so that the gas expands. Heat is gained from the source and the process is isothermal at constant temperature T₁. In this process the volume of the gas changes from V1 to V2 and the pressure changes from P1 to P2. This process is represented by AB in the indicator diagram (Fig.).

During this process, the quantity of heat absorbed from the source is Q1 and W1 is the corresponding amount of work done by the gas.

Q1 = W1 = ∫_v1^v2PdV = RT₁log_e(V₂/V₁) = area ABGEA ...(1)

Adiabatic expansion

The cylinder is taken from the source and is placed on the insulting stand and the piston is moved further so that the volume of the gas changes from V₂ to V₃ and the pressure changes from P₂ to P₃. This adiabatic expansion is represented by BC. Since the gas is thermally insulated from all sides no heat can be gained from the surroundings. The temperature of the gas falls from T₁ to T₂.

Let W₂ be the work done by the gas in expanding adiabatically.

∴ W2 = ∫_v1^v2PdV = R/(γ-1)  .  (T₁-T₂)= Area BCHGB ...(2)

Isothermal compression

The cylinder is now placed on the sink at a temperature T₂. The piston is moved slowly downward to compress the gas isothermally. This is represented by CD. Let (V₄, P₄) be the volume and pressure corresponding to the point D. Since the base of the cylinder is conducting the heat produced during compression will pass to the sink so that, the temperature of the gas remains constant at T₂. Let Q₂ be the amount of heat rejected to the sink and W₃ be the amount of work done on the gas in compressing it isothermally.

Q₂ = W₃ = ∫_v1^v2-PdV = -RT₂log_e(V₄/V₃) = - area ABGEA ...(1)

The negative sign indicates that work is done on the working substance.

Q₂ = RT₂ log_e(V₃/V₄)

Adiabatic compression

The cylinder is now placed on the insulating stand and the piston is further moved down in such a way that the gas is compressed adiabatically to its initial volume V₁ and pressure P₁. As the gas is insulated from all sides heat produced raises the temperature of the gas to T₁. This change is adiabatic and is represented by DA. Let W₄ be the work done on the gas in compressing it adiabatically from a state D (V₄ , P₄) to the initial state A (V₁, P₁).

∴ W₄ = - ∫_v1^v2PdV = -R/(γ-1)  .  (T₁-T₂)= Area BCHGB ...(4)

The negative sign indicates that work is done on the working substance.

Work done by the engine per cycle

Total work done by the gas during one cycle of operation is (W₁ + W₂).

Total work done on the gas during one cycle of operation is (W₃ + W₄).

∴ Net work done by the gas in a complete cycle

W = W₁ + W₂ ? (W₃ + W₄)

But W₂ = W₄

 ∴ W = W₁ ? W₃

W = Q₁ ? Q₂

Also, W = Area ABGEA + Area BCHGB - Area CDFHC - Area DAEFD

 (i.e) W = Area ABCDA

Hence in Carnot heat engine, net work done by the gas per cycle is numerically equal to the area of the loop representing the cycle.

Efficiency of Carnot?s engine

η= Heat converted into work /  Heat drawn from the source = Q₁-Q₂/Q₁

η= 1 ? Q₂/Q₁

But

 Q₁/Q₂  = W₁/W₃ = RT₁log(V₂/V₁)  /  RT₂log(V₃/V₄)

= T₁log(V₂/V₁)  /  T₂log(V₃/V₄)  ???(5)

Since B and C lie on the same adiabatic curve BC

T₁V₂^γ-1 = T₂V₃^γ-1 (∵ TV^{γ - 1} = constant) where γ = C_p/C_v

T₁/T₂ = V₃^γ-1 / V₂^γ-1  ???(6)

Similarly D & A lie on the same adiabatic curve DA

T₁V₁^γ-1 = T₂V₄^γ-1

T₁/T₂ = V₄^γ-1 / V₁^γ-1  ???(7)

From (6) & (7)

V₃^γ-1 / V₂^γ-1 = V₄^γ-1 / V₁^γ-1

V₃/V₂ = V₄/V₁

Or

V₂/V₁ = V₃/V₄   ?????..(8)

substituting equation (8) in equation (5)

(i.e) Q₁/Q₂ = T₂/T₁

We have η= 1-(Q₂/Q₁) = 1-(T₂/T₁)

η= T₁-T₂ / T₁

Inferences

Efficiency of Carnot?s cycle is independent of the working substance, but depends upon the temperatures of heat source and sink.

Efficiency of Carnot?s cycle will be 100% if T₁ = ∞ or T₂ = 0 K. As neither the temperature of heat source can be made infinite, nor the temperature of the sink can be made 0 K, the inference is that the Carnot heat engine working on the reversible cycle cannot have 100% efficiency.