Calibrating Signals

Calibrating Signals

Signals are measured using equipment or instruments that must be properly cali- brated if S_meas is to be free of determinate errors. Calibration is accomplished against a standard, adjusting S_meas until it agrees with the standard’s known signal. Several common examples of calibration are discussed here.

When the signal is a measurement of mass, S_meas is determined with an analyti- cal balance. Before a balance can be used, it must be calibrated against a reference weight meeting standards established by either the National Institute for Standards and Technology or the American Society for Testing and Materials. With an elec- tronic balance the sample’s mass is determined by the current required to generate an upward electromagnetic force counteracting the sample’s downward gravita- tional force. The balance’s calibration procedure invokes an internally programmed calibration routine specifying the reference weight to be used. The reference weight is placed on the balance’s weighing pan, and the relationship between the displace- ment of the weighing pan and the counteracting current is automatically adjusted.

Calibrating a balance, however, does not eliminate all sources of determinate error. Due to the buoyancy of air, an object’s weight in air is always lighter than its weight in vacuum. If there is a difference between the density of the object being weighed and the density of the weights used to calibrate the balance, then a correc- tion to the object’s weight must be made. An object’s true weight in vacuo, W_v, is related to its weight in air, W_a, by the equation

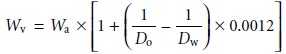
where D_o is the object’s density, D_w is the density of the calibration weight, and 0.0012 is the density of air under normal laboratory conditions (all densities are in units of g/cm3). Clearly the greater the difference between D_o and D_w the more seri- ous the error in the object’s measured weight.

The buoyancy correction for a solid is small, and frequently ignored. It may be significant, however, for liquids and gases of low density. This is particularly important when calibrating glassware. For example, a volumetric pipet is calibrated by carefully filling the pipet with water to its calibration mark, dispensing the water into a tared beaker and determining the mass of water transferred. After correcting for the buoyancy of air, the density of water is used to calculate the volume of water dispensed by the pipet.

Balances and volumetric glassware are examples of laboratory equipment. Lab- oratory instrumentation also must be calibrated using a standard providing a known response. For example, a spectrophotometer’s accuracy can be evaluated by measuring the absorbance of a carefully prepared solution of 60.06 ppm K₂Cr₂O₇ in 0.0050 M H₂SO₄, using 0.0050 M H₂SO₄ as a reagent blank. The spectrophotome- ter is considered calibrated if the resulting absorbance at a wavelength of 350.0 nm is 0.640 ± 0.010 absorbance units. Be sure to read and carefully follow the calibra- tion instructions provided with any instrument you use.