Chapter: Cryptography and Network Security Principles and Practice : One Symmetric Ciphers : Block Ciphers and the Data Encryption Standard
A DES(Data Encryption Standard) Example
A DES EXAMPLE
We now work through an example and consider some of its implications.
Although you are not expected to duplicate the example by hand, you will find
it informative to study the hex patterns that occur from one step to the next.
For this example, the plaintext is a hexadecimal palindrome. The plaintext, key, and resulting
ciphertext are as follows:

Results
Table 3.5 shows the progression of the algorithm. The first row
shows the 32-bit values of the left
and right halves of data after the initial permutation. The next 16 rows show the results after each round.
Also shown is the value of the 48-bit subkey generated
for each round.
Note that Li = Ri - 1. The final row shows the left- and right-hand values after the
inverse initial permutation. These two values com- bined form the ciphertext.
The Avalanche Effect
A desirable property
of any encryption algorithm is that a small change in either the
plaintext or the key should produce a significant change in the ciphertext. In partic-
ular, a change in one bit of the plaintext or one bit of the key should produce
a change in many bits of the ciphertext. This is referred
to as the avalanche effect.
If the change were small, this
might provide a way to reduce the size of the plaintext or key space to be searched.
Using the example
from Table 3.5, Table 3.6 shows the result when the fourth bit of the plaintext
is changed, so that the plaintext is 12468aceeca86420. The second column
of the table shows the intermediate 64-bit
values at the end of each
round for the two plaintexts. The third
column shows the number of bits that differ
between the two intermediate values. The table
shows that, after just three rounds,
18 bits differ between the two blocks.
On completion, the two ciphertexts differ in 32 bit positions.
Table 3.5 DES
Example


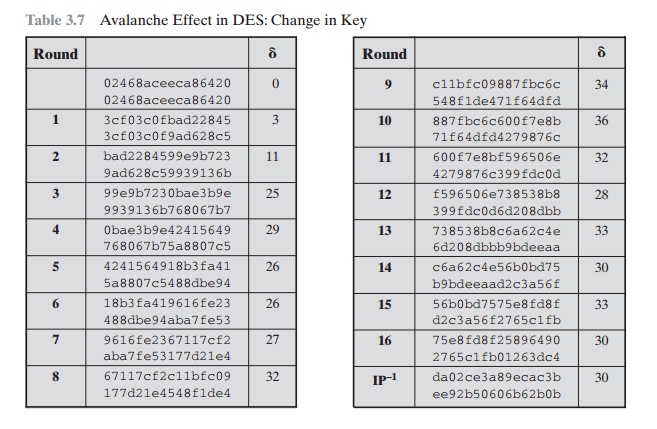
Table 3.7 shows a similar
test using the original
plaintext of with two keys that
differ in only the fourth
bit position: the original key, 0f1571c947d9e859, and the altered
key, 1f1571c947d9e859. Again, the results show that about half of the bits in the ciphertext
differ and that the avalanche effect is pronounced
after just a few rounds.
Table
3.7 Avalanche Effect in DES: Change in Key
Related Topics