Solved Problems: Civil - Mechanics Of Fluids - Dimensional Analysis And Model Studies

Problem 1

The resisting force of (R) of a supersonic flight can be considered as dependent upon the length of aircraft 'l', velocity 'V', air viscosity '?', air density '?', and bulk modulus of air 'k'. Express the functional relationship between these variables and the resisting force.

Solution:

Step 1. R = f ( l, V, ?, ?, k ) ? ( R, l, V, ?, ?, k) = 0

Number of variables, n = 6 Number of primary variable, m = 3

Number of ? terms = n - m = 6 - 3 = 3 f (?1, ?2, ?3) = 0

Step 2.  Assume l, V and ? to be the repeating variables.

?1  = l^x, V^y, ?^z,R

M^OL^OT^O = [ L]^X [ LT^-1] ^y [ML^-3]^z [MLT^-2]

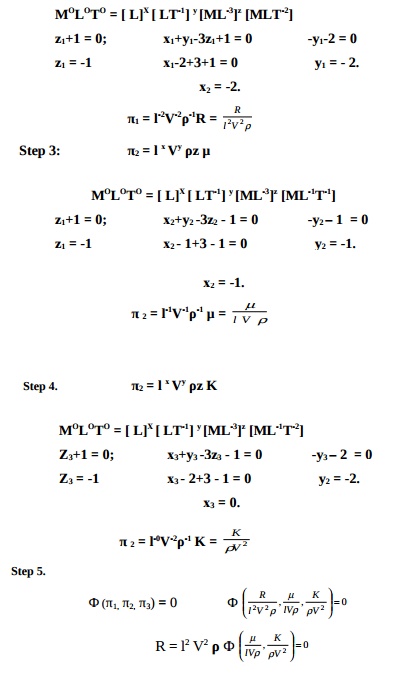
Problem 2

A Ship is 300m long moves in seawater, whose density is 1030 kg/m³, A 1:100 model of this to be tested in a wind tunnel. The velocity of air in the wind tunnel around the model is 30m/s and the resistance of the model is 60N. Determine the velocity of ship in seawater and also the resistance of the ship in sea water. The density of air is given as 1.24 kg/m³. Take the Kinematic viscosity of seawater and air as 0.012 stokes and 0.018 stokes respectively.

Given:

For prototype,                                                             

Length                                                                          Lp = 300m

Fluid                                                                              = Sea water

Density of water                                                           = 1030 kg/m³

Problem 3

A 7.2 m height and 15m long spill way discharges 94 m³/s discharge under a head of 2.0m. If a 1:9 scale model of this spillway is to be constructed, determine model dimensions, head over spillway model and the model discharge. If model experience a force of 7500N (764.53Kgf), determine force on the prototype.

Given:

For prototype: height  hp = 7.2m

Length,                         Lp = 15m

Discharge                    Qp = 94 m³/s

Head,                                                                            Hp = 2.0m

Size of model = 1/9. of the size of prototype

Linear scale ratio,        Lr = 9

Force experienced by model  Fp = 7500N

Find : (i) Model dimensions i.e., height and length of model (hm and Lm) (ii). Head over model i.e., Hm

(iii). Discharge through model i.e., Qm (iv). Force on prototype (i.e., Fp)

(i). Model dimensions ( hm and Lm )

hp/ hm  = Lp/ Lm = Lr = 9

hm = hp / 9 = 7.2 / 9 = 0.8 m Lm = Lp / 9 = 15 / 9 = 1.67 m.

(ii). Head over model (Hm)

hp/ Hm = Lr = 9

Hm = Hp / 9 = 2/9 = 0.222 m. (iii). Discharge through model (Qm)

Using equation we get, Qp / Qm = Lr^2.5

Qm = (Qp / Lr^2.5) = 94 / 9^2.5 = 0.387 m³/s. (iv). Force on the prototype(Fp)

Using Fr = Fp / Fm = Lr³

Fp = Fm X Lr³ 7500X9³ = 5467500N.

Problem 4

A quarter scale turbine model is tested under a head of 12m. The full-scale turbine is to work under a head of 30m and to run at 428 rpm. Find N for model. If model develops 100 kW and uses 1100 l/s at this speed, what power will be obtained from full scale turbine assuming its n is 3% better than that of model.

Solution :

Dm / Dp = 1/4 ; Hm = 30 m; Np = 428 rpm. w.k.t.