Chapter: Mathematics (maths) : Random Processes
Important Short Objective Questions and Answers: Random Processes
Markov Processes and Markov chains
1. Define Random
processes and give an example of a random process. Answer:
A Random process is a collection of R.V {X
(s,t)}that are functions of a
real variable
namely
time t where s ∈ S and t ∈T
Example:
X
(t)
=
Acos(ωt +
θ )
where θ
is
uniformly distributed in ( ,20π
)
where A and
2. State the four classifications of Random processes.
Sol: The Random
processes is classified into four types
(i)Discrete
random sequence
If both T and S are discrete then Random processes is called a discrete Random sequence.
(ii)Discrete
random processes
If T is continuous and S is discrete then Random processes is called a Discrete Random
processes.
(iii)Continuous
random sequence
If T is discrete and S is continuous then Random processes is called a Continuous Random sequence.
(iv)Continuous
random processes
If T &S are continuous then Random processes is called a continuous Random processes.
3. Define
stationary Random processes.
If certain probability distributions or averages do not depend on t, then the random process
{X (t)}is
called stationary.
4.
Define first order stationary Random processes.
A
random processes {X
(t)}is said to be a first order SSS process
if
f (x1
,t1 +
δ )
=
f (x1
,t1 ) (i.e.) the first order density of a
stationary process {X (t)}
is
independent of time t
5.
Define second order stationary Random processes
A RP {X
(t)} is said to be second order SSS if f
(x1, x2 ,t1 ,t2
) =
f (x1 , x2 ,t1 +
h,t2 + h) where f
(x1, x2 ,t1,t2
) is the joint PDF of {X
(t1 ), X (t2 )}.
6.
Define strict sense stationary Random processes
Sol: A RP {X
(t)} is called a SSS process if the joint
distribution X (t1 )X (t21 )X
(t3 ).........X (tn ) is the same as
that of
X (t1
+
h)X
(t2 +
h)X
(t3 +
h).........X
(tn + h)
for allt1 ,t2 ,t3
.........tn and h >0 and for n ≥
1.
7.
Define wide sense stationary Random processes
A RP {X
(t)}is called WSS if E{X
(t)} is constant and E[X
(t)X (t +τ
)]=
Rxx (τ
) (i.e.) ACF is a function of τ
only.
8.
Define jointly strict sense stationary Random processes
Sol: Two real valued
Random Processes {X
(t)}and
{Y(t)}
are
said to be jointly stationary in the strict sense if the joint
distribution of the {X
(t)}and {Y(t)}
are invariant under translation
of
time.
9.
Define jointly wide sense stationary Random processes
Sol: Two real valued Random Processes {X (t)}and {Y(t)} are said to be jointly stationary in the wide sense if each process is individually a WSS process and RXY (t1 ,t2 ) is a function of t1 ,t2 only.
10. Define Evolutionary Random processes and give an example.
Sol: A Random processes that
is not stationary in any sense is called an Evolutionary process.
Example: Poisson process.
11. If {X
(t)}
is a WSS with auto correlation R(τ ) =
Ae−α τ , determine the second order
moment of the random variable X (8) – X (5).
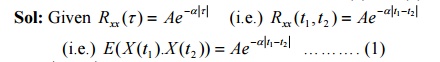
∴
E(X
2 (t))=
E(X
(t)X (t)) =
Rxx (t,t) =
Ae−α
(0) =
A
∴ E(X 2 (8)) = A & E(X 2 (5)) = A ∴ E(X (8)X (5)) = Rxx ( 5,)8= A.e−3α .
Now second
order moment of {X
(8) −
X (5)} is given by
E(X
(8) − X (5))2
=
E(X
2 (8) +
X 2 (5)
−
2X
(8)X (5))
= E(X
2 (8)) +
E(X
2 (5)) −
2E(X
(8)X (5))
= A
+
A −
2Ae−3α =
2A
1(−
e−3α )
12.Verify whether the sine wave process{X
(t)},
where X (t)
=
Y
cosωt where Y is
uniformly distributed in (0,1) is a SSS process.
Sol: F(x) =
P(X (t) ≤ x) = P(Y cosωt ≤ x)

If {X(t)} is to be a SSS process, its
first order density must be independent of t. Therefore, {X(t)}is not a SSS process.
13. Consider a random
variable Z(t) =
X1
cosω0t
−
X
2 sinω0t
where X1
and X2
are independent Gaussian random variables with zero mean and variance σ 2
find E(Z) and E( Z 2
)
Sol: Given E(X1
) = 0 =
E(X
2 ) &Var(X1 ) =
σ 2
=
Var(X
2 )
⇒ E(X12
) = σ 2
=
E(X
2 2 )
E(Z)
=
E(X1
cosω0t
−
X 2 sinω0t)
=
0
E(Z 2
) = E(X1
cosω0t
−
X 2 sinω0t)2
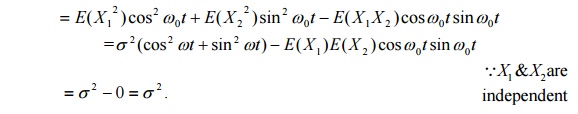
14.Consider the random
process X (t)
=
cos(ω0t
+
θ )
where θ is uniformly
distributed in (−π ,π ) .Check whether
X(t) is stationary or not?
Answer:
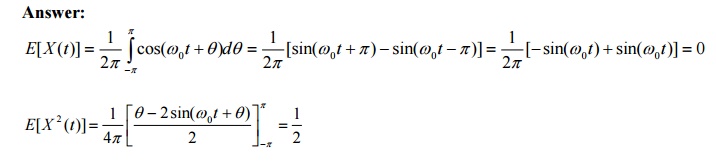
15. Define Markov Process.
Sol: If for t1 < t2 <
t3 < t4 ............ < tn < t
then
P(X (t)
≤
x /
X (t1 ) =
x1 ,
X (t2 ) =
x2 ,..........X
(tn ) =
xn ) =
P(X
(t) ≤ x /
X (tn ) = xn
)
Then the process {X
(t)}is called a Markov process.
16. Define Markov chain.
Sol: A Discrete parameter Markov process is called
Markov chain.
17. Define one step transition
probability.
Sol:

Yes it is irreducible since each state can be
reached from any other state

Therefore the chain is irreducible.
20 State the postulates of a Poisson
process.
Let {X
(t)} = number of times an event A say,
occurred up to time ‘t’ so that the sequence {X
(t)}, t ≥
0 forms a Poisson process with parameter λ
.
(i)
P[1 occurrence in (t,t + ∆t)
]=λ∆t
(ii)
P[0 occurrence in (t,t + ∆t)
]=1-λ∆t
(iii)
P[2 or more occurrence in (t,t
+
∆t)
]=0
(iv)
X(t) is independent of the number of
occurrences of the event in any interval prior and after the interval (0,t).
(v)
The probability that the event occurs a
specified number of times in (t0,t0+t) depends only on t,
but not on t0.
20.State
any two properties of Poisson process Sol: (i) The Poisson
process is a Markov process
(ii) Sum
of two independent Poisson processes is a Poisson process
(iii) The
difference of two independent Poisson processes is not a Poisson process.
21.If the customers arrived at a counter in accordance with a Poisson process with a mean rate of 2 per minute, find the probability that the interval between two consecutive arrivals is more than one minute.
Sol: The interval T
between 2 consecutive arrivals follows an exponential distribution with
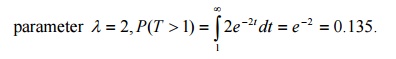
22.A bank receives on an average λ =
6
bad checks per day, what are the probabilities that it will receive (i) 4 bad
checks on any given day (ii) 10 bad checks over any 2 consecutive days.

23.Suppose the customers arrive at a
bank according to a Poisson process with a mean rate of 3 per minute. Find the
probability that during a time interval of 2 minutes exactly 4 customers arrive
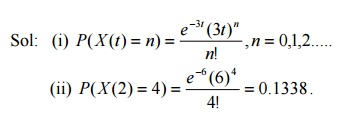

25.Customers arrive a large store
randomly at an average rate of 240 per hour. What is the probability that
during a two-minute interval no one will arrive.
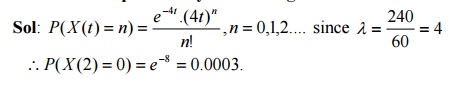
26.The no of arrivals at the reginal
computer centre at express service counter between 12 noon and 3 p.m has a
Poison distribution with a mean of 1.2 per minute. Find the probability of no
arrivals during a given 1-minute interval.

27. For the sine wave process X
(t)
=
Y
cosωt,−∞
<
t
<
∞
where ω = constant, the
amplitude Y is a random variable with uniform distribution in the interval 0
and 1.check wheather the process is stationary or not.
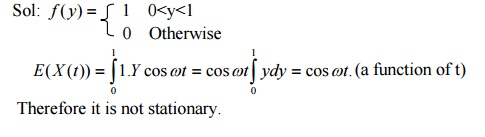
Therefore
it is not stationary.
28.
Derive the Auto Correlation of Poisson Process.
Sol:
Rxx (t1 ,t2 ) =
E[X
(t1 )X (t2 )]
R
xx
(t1 ,t2 ) =
E[X
(t1 ){X
(t2 ) − X (t1
) +
X (t1 )}]
=E[X
(t1
){X
(t2
) − X (t1
)}]+
E[X
2 (t1
)]
=E[X
(t1
)]E[X
(t2
) − X (t1
)]+
E[X
2 (t1
)]
Since
X (t) is a Poisson process, a process of independent increments.
∴ Rxx (t1
,t2 ) =
λt1
(λt2
−
λt1
)
+
λ1t1
+
λ12t12
if
t2 ≥ t1
⇒ Rxx (t1
,t2 ) =
λ2t1t2
+
λt1
if
t2 ≥ t1
(or)
⇒ Rxx (t1
,t2 ) = λ2t1t2
+
λ min{t1
,t2 }
29.
Derive the Auto Covariance of Poisson process
Sol:
C(t1 ,t2 ) =
R(t1 ,t2 ) −
E[X
(t1 )]E[X
(t2 )]
= λ2t1t2 + λt1 − λ2t1t2 = λt1 if t2 ≥ t1
∴ C(t1,t2
) = λ min{t1,t2}
30.Define
Time averages of Random process.
Sol: The time averaged mean of a sample function X
(t) of a random process{X
(t)} is

mean and variance of X(10)-X(6).
Answer:
X(10)-X(6)
is also a normal R.V with mean µ(10)
−
µ(6) =
0
and Var[X (10) −
X (6)]
=
var{X
(10)}+ var{X (6)}−
2cov{X
(10), X (6)}
= C(10,10) + C(
6,)6−
2C(10
6,)
= 16 +16 − 2×16e−4 = 31.4139
33.Define a Birth process.
Answer:
A Markov process {X(t)} with state space S={1,2…..}
such that

34.Define
Ergodic Random Process.
Sol: A random process {X
(t)}is said to be Ergodic Random Processif
its ensembled averages
are
equal to appropriate time averages.
35.Define
Ergodic state of a Markov chain.
Sol:
A non null persistent and aperiodic state is called an ergodic state.
36.Define
Absorbing state of a Markov chain.
Sol: A state i is called an absorbing state if and
only if Pij = 1 and Pij
=
0 for i ≠ j
37.Define irreducible
The process is
stationary as the first and second moments are independent of time. State any
four properties of Autocorrelation function.
Answer:
i) RXX
(−τ ) =
RXX (τ
)
ii) R(τ ) ≤
R(0)
iii) R(τ ) is continuous
for all τ
iv) if
RXX (−τ
) is AGF of a stationary random process {X(t)} with no periodic
![]()
![]() components, then µX
2 = lim →∞ R(τ )
components, then µX
2 = lim →∞ R(τ )
38.What
do you mean by absorbing Markov chain? Give an example.
Sol:
A State I of a Markov chain is said to be an absorbing state if Pii
=
1(i.e.) it is
impossible to leave it .A Markov chain is said to be
absorbing if it has at least one absorbing state.
Eg: The tpm of an absorbing Markov chain is
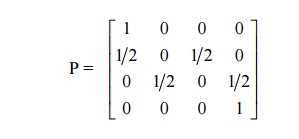
39.Define
Bernoulli Process.
Sol: The Bernoulli random variable is defined as X
(ti ) = ti
which takes two values 0 and 1 with the time index ti such
that {X
(ti , s) : i =
......... −1 1,,0,......;s =
1,}0
40State the properties of Bernoulli
Process. Sol: (i) It is a Discrete process
(ii) It
is a SSS process
(iii) E(Xi
) = p,
E(X 2 ) =
p and
Var(Xi ) =
p 1(−
p)
41.Define Binomial Process
Sol:
It is defined as a sequence of partial sums {Sn
},n
=
,13,.....2 where
Sn
=
X1 +
X 2 +
........
+
X n
42.State
the Basic assumptions of Binomial process
Sol: (i) The time is assumed to be
divided into unit intervals. Hence it is a discrete time process.
(ii) At
most one arrival can occur in any interval
(iii) Arrivals
can occur randomly and independently in each interval with probability p.
43.Prove that Binomial process is a
Markov process
Sol: Sn
=
X1 + X 2 +
........ + X n Then Sn
=
Sn−1
+
X n
∴
P(Sn
=
m /
Sn−1
=
m)
=
P(X
n = 0)
=
1−
p.
Also P(Sn =
m / Sn−1
=
m −1) =
P(X n =
1) =
p.
(i.e.) the probability distribution of Sn
,depends only on Sn−1
.The process is Markovian process.
44.
Define Sine wave process.
Sol:
A sine wave process is represented as X (t) =
Asin(ωt
+
θ ) where the amplitude
A ,or frequency ω
or phase θ or any
combination of these three may be random.
It is also represented as X (t) =
Acos(ωt
+
θ ) .
45.Prove that sum of two independent
Poisson process is also Poisson.
Sol: Let X (t) =
X1 (t) +
X 2 (t)
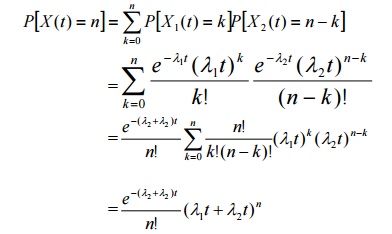
Therefore X (t) =
X1 (t) +
X 2 (t) is a Poisson process with parameter (λ1 +
λ2
)t
1.. The t.p.m of a Marko cain with three states 0,1,2 is P and the initial state distribution is Find (i)P[X2=3] ii)P[X3=2, X2=3, X1=3, X0=2]
2. Three boys A, B, C are throwing a ball each other. A always throws the ball to B and B always throws the ball to C, but C is just as likely to throw the ball to B as to A. S.T. the process is Markovian. Find the transition matrix and classify the states
3. A housewife buys 3 kinds of cereals A, B, C. She never buys the same cereal in successive weeks. If she buys cereal A, the next week she buys cereal B. However if she buys P or C the next week she is 3 times as likely to buy A as the other cereal. How often she buys each of the cereals?
4. A man either drives a car or catches a train to go to office each day. He never goes 2 days in a row by train but if he drives one day, then the next day he is just as likely to drive again as he is to travel by train. Now suppose that on the first day of week, the man tossed a fair die and drove to work if a 6 appeared. Find 1) the probability that he takes a train on the 3rd day. 2). The probability that he drives to work in the long run.


Related Topics