Correlation and Spectral Density

CORRELATION AND SPECTRAL DENSITY

Introduction

Auto Correlation functions and Properties

Cross Correlation functions and Properties

Power spectral density and Properties

Cross spectral density and Properties

Introduction

The power spectrum of a time series x(t) describes how the variance of the data x(t) is distributed over the frequency components into which x(t) may be decomposed. This distribution of the variance may be described either by a measure µ or by a statistical cumulative distribution function S(f) = the power contributed by frequencies from 0 upto f. Given a band of frequencies [a, b) the amount of variance contributed to x(t) by frequencies lying within the interval [a,b) is given by S(b) - S(a). Then S is called the spectral distribution function of x.

The spectral density at a frequency f gives the rate of variance contributed by frequencies in the immediate neighbourhood of f to the variance of x per unit frequency.

1 Auto Correlation of a Random Process

Let X(t1) and X(t2) be the two given random variables. Then auto correlation is

RXX (t1, t2) = E[X(t1) X(t2)] Mean Square Value

Putting t1 = t2 = t in (1)

RXX (t, t) = E[X(t) X(t)]

⇒          RXX (t, t) = E[X²(t)]

Which is called the mean square value of the random process.

Auto Correlation Function

Definition: Auto Correlation Function of the random process {X(t)} is

RXX = (τ) = E{(t) X(t+τ)}

Note: RXX (τ) = R(τ) = RX (τ)

PROPERTY: 1

The mean square value of the Random process may be obtained from the auto correlation function.

RXX(τ), by putting τ = 0.

is known as Average power of the random process {X(t)}.

PROPERTY: 2

RXX(τ) is an even function of τ.

RXX (τ) = RXX (-τ)

PROPERTY: 3

If the process X(t) contains a periodic component of the same period.

PROPERTY: 4

If a random process {X(t)} has no periodic components, and E[X(t)] = X then

PROPERTY: 5 

 The auto correlation function of a random process cannot have an arbitrary shape. 

SOLVED PROBLEMS ON AUTO CORRELATION

Example : 3

Express the autocorrelation function of the process {X'(t)} in terms of the auto correlation function of process {X(t)}

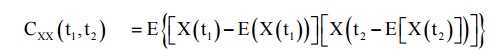
2 CORRELATION COEFFICIENT

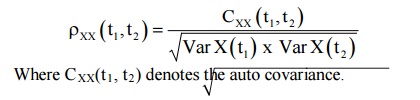
3 CROSS CORRELATION

Cross correlation between the two random process {X(t)} and {Y(t)} is defined as RXY (t1, t2) = E[X(t1) Y(t2)] where X(t1) Y(t2) are random variables.

4 CROSS COVARIANCE

Let {X(t)} and {Y(t)} be any two random process. Then the cross covariance is defined as

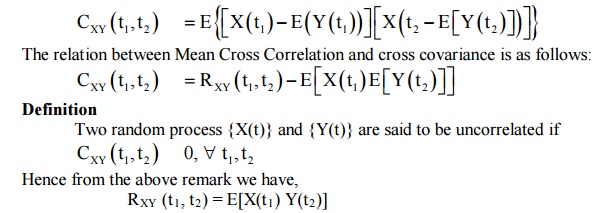
4.1 CROSS CORRELATION COEFFICIENT

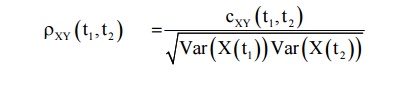
4.2 CROSS CORRELATION AND ITS PROPERTIES

Let {X(t)} and {Y(t)} be two random. Then the cross correlation between them is also defined as

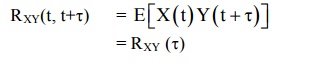
PROPERTY : 1

RXY (τ) = RYX (–τ)

PROPERTY : 2

PROPERTY : 3

If {X(t)} and {Y(t)} are two random process then,

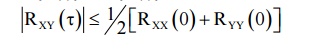
SOLVED PROBLEMS ON CROSS CORRELATION

Example:4.4.1

Two random process {X(t)} and {Y(t)} are given by X(t) = A cos (ωt+θ), Y(t) = A sin (ωt + θ) where A and ω are constants and 'θ' is a uniform random variable over 0 to 2π. Find the cross correlation function.

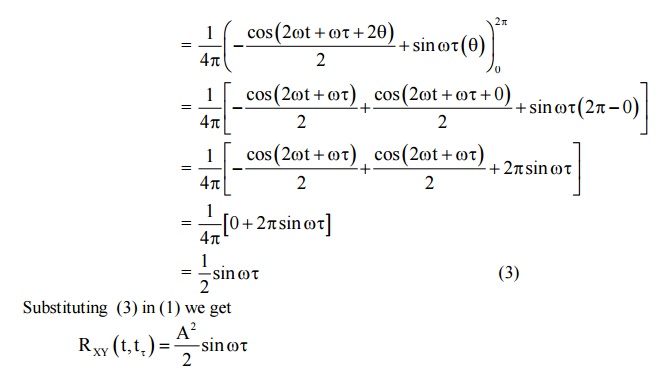
5 SPECTRAL DENSITIES (POWER SPECTRAL DENSITY)

INTRODUCTION

(i) Fourier Transformation

(ii) Inverse Fourier Transform

(iii) Properties of Auto Correlation Function

(iv)Basic Trigonometric Formula

(v) Basic Integration

5.1 SPECIAL REPRESENTATION

Let x(t) be a deterministic signal. The Fourier transform of x(t) is defined as

Definition

The average power P(T) of x(t) over the interval (-T, T) is given by

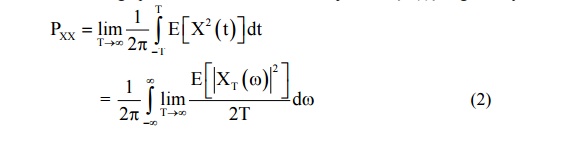
Definition

The average power PXX for the random process {X(t)} is given by

6 POWER SPECTRAL DENSITY FUNCTION

Definition

If {X(t)} is a stationary process (either in the strict sense or wide sense) with auto correlation function RXX(τ), then the Fourier transform of RXX(τ) is called the power spectral density function of {X(t)} and is denoted by SXX(ω) or S(ω) or SX(ω). 

SXX(ω)= Fourier Transform of RXX (τ)

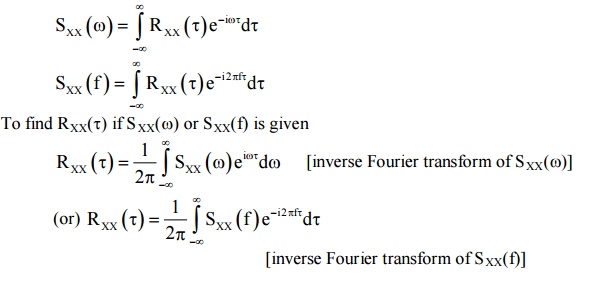
6.1 WIENER KHINCHINE RELATION

7 PROPERTIES OF POWER SPECTRAL DENSITY FUNCTION

Property 1:

The value of the spectral density function at zero frequency is equal to the total area under the group of the auto correlation function.

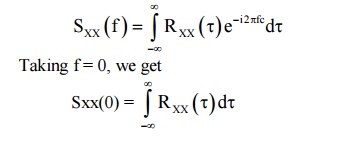
WORKEDOUT EXAMPLES

Example : 3

Express the autocorrelation function of the process {X'(t)} in terms of the auto correlation function of process {X(t)} 

Solution