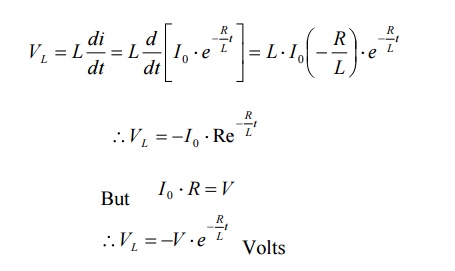Chapter:
Analysis of undriven(source free) series RC and RL circuits
Discharging of capacitor through resistor in source free series RC circuit. Or Analysis of undriven or source free series RC circuits.
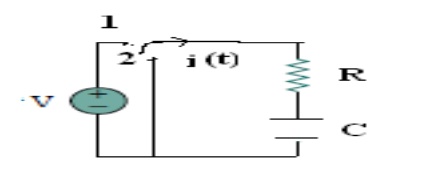
Consider network shown in fig. the switch k is moved from position
1 to 2 at reference time t = 0.
Now before switching take place, the capacitor C is fully charged
to V volts and it discharges through resistance R. As time passes, charge and
hence voltage across capacitor i.e. Vc decreases gradually and hence
discharge current also decreases gradually from maximum to zero exponentially.
After
switching has taken place, applying kirchoff’s voltage law,
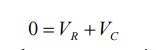
Where VR
is voltage across resistor and VC is voltage across capacitor.
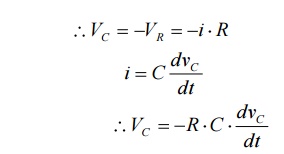
Above
equation is linear, homogenous first order differential equation. Hence
rearranging we have,
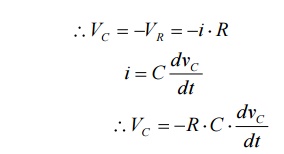
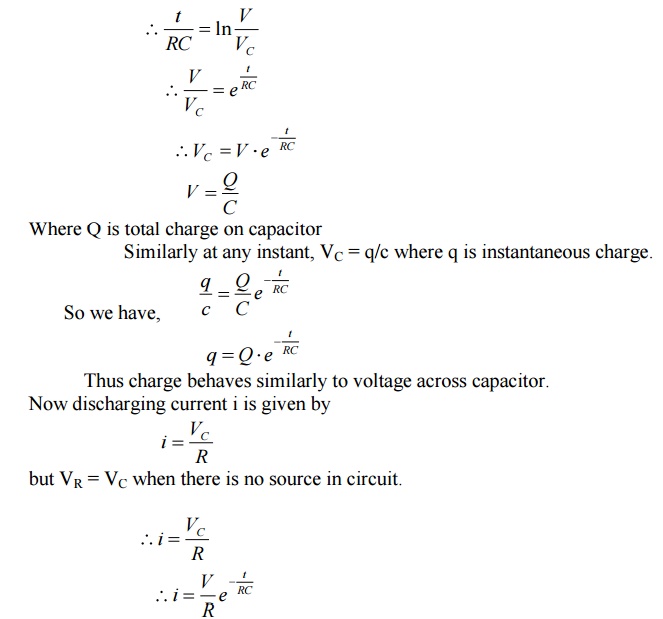
The above expression is nothing but discharge current of capacitor.
The variation of this current with respect to time is shown in fig.
This shows that the current is exponentially decaying. At point P
on the graph. The current value is (0.368) times its maximum value. The
characteristics of decay are determined by values R and C, which are 2
parameters of network.
For this
network, after the instant t = 0, there is no driving voltage source in
circuit, hence it is called undriven RC circuit.

Analysis of undriven series RL circuits (or) Analysis of source free series RL circuits
Current decay in source free series RL circuit:
-
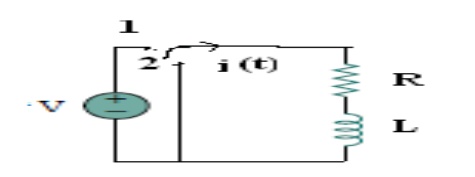
At t = 0-
, switch k is kept at position ‘a’ for very long time. Thus, the network is in
steady state. Initial current through inductor is given as,
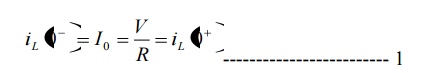
Because current through inductor can not change
instantaneously
Assume
that at t = 0 switch k is moved to position ‘b’,

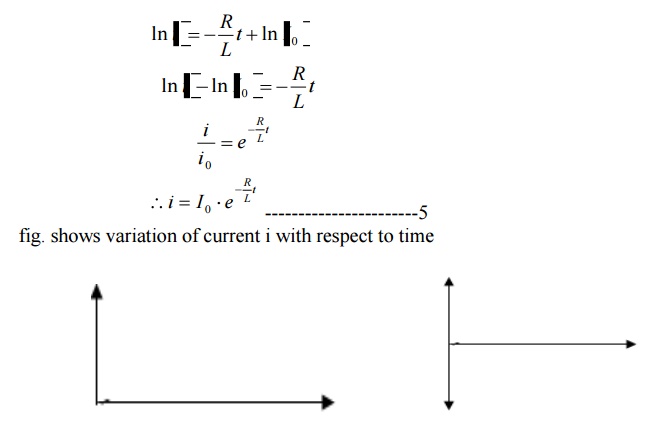
From the graph, H is clear that current is exponentially decaying.
At point P on graph. The current value is (0.363) times its maximum value. The
characteristics of decay are determined by values R and L which are two
parameters of network.
The
voltage across inductor is given by