Chapter: Fundamentals of Database Systems : Transaction Processing, Concurrency Control, and Recovery : Concurrency Control Techniques
Two-Phase Locking Techniques for Concurrency Control
Two-Phase Locking Techniques for Concurrency Control
Some of the main techniques used to control concurrent execution of
transactions are based on the concept of locking data items. A lock is a variable associated with a
data item that describes the status of the item with respect to possible
operations that can be applied to it. Generally, there is one lock for each
data item in the data-base. Locks are used as a means of synchronizing the
access by concurrent transactions to the database items. In Section 22.1.1 we
discuss the nature and types of locks. Then, in Section 22.1.2 we present
protocols that use locking to guarantee serializability of transaction schedules.
Finally, in Section 22.1.3 we describe two problems associated with the use of
locks—deadlock and starvation—and show how these problems are handled in
concurrency control protocols.
1. Types of Locks and
System Lock Tables
Several types of locks are used in concurrency control. To introduce
locking concepts gradually, first we discuss binary locks, which are simple,
but are also too restrictive for database concurrency control purposes, and so are
not used in practice. Then we discuss
shared/exclusive locks—also known as read/write locks—which provide more
general locking capabilities and are used in practical database locking
schemes. In Section 22.3.2 we describe an additional type of lock called a certify lock, and show how it can be
used to improve performance of locking protocols.
Binary Locks. A binary lock can have two states or values: locked and unlocked (or 1 and 0, for simplicity). A distinct lock is associated with each
database item X. If the value of the
lock on X is 1, item X cannot be accessed by a database
operation that requests the item. If the value of the lock on X is 0, the item can be accessed when
requested, and the lock value is changed to 1. We refer to the current value
(or state) of the lock associated with item X
as lock(X).
Two operations, lock_item and unlock_item, are used with binary locking. A transaction requests access to an item
X by first issuing a lock_item(X) operation. If LOCK(X) = 1, the transaction is forced to
wait. If LOCK(X) = 0, it is set to 1 (the transaction
locks the item) and the transaction
is allowed to access item X. When the
transaction is through using the item, it issues an unlock_item(X) operation,
which sets LOCK(X) back to 0 (unlocks the item) so that X may be accessed by other transactions.
Hence, a binary lock enforces mutual
exclusion on the data item. A description of the lock_item(X) and unlock_item(X) operations is shown in
Figure 22.1.
lock_item(X):
B: if LOCK(X) = 0 (* item is
unlocked *)
then LOCK(X) ←1 (* lock the item *)
else
begin
wait (until LOCK(X) = 0
and the lock manager wakes up the transaction);
go to B
end;
unlock_item(X):
LOCK(X) ← 0; (* unlock the item *)
if any transactions are waiting
then wakeup one of the waiting transactions;
Figure 22.1 Lock and unlock operations for binary locks.
Notice that the lock_item and unlock_item operations must be implemented as indivisible units (known as critical sections in operating
systems); that is, no interleaving should be allowed once a lock or unlock
operation is started until the operation terminates or the transaction waits.
In Figure 22.1, the wait command within the lock_item(X) operation is usually implemented by
putting the transaction in a waiting queue for item X until X is unlocked and
the transaction can be granted access to it. Other transactions that also want
to access X are placed in the same
queue. Hence, the wait command is considered to be outside the lock_item operation.
It is quite simple to implement a binary lock; all that is needed is a
binary-valued variable, LOCK, associated with each data item X in the database. In its simplest form,
each lock can be a record with three fields: <Data_item_name, LOCK, Locking_transaction> plus a queue for transactions that are waiting to access the item. The system needs to maintain only
these records for the items that are currently locked in a lock table, which could be organized as
a hash file on the item name. Items not in the lock table are considered to be
unlocked. The DBMS has a lock manager
sub-system to keep track of and control access to locks.
If the simple binary locking scheme described here is used, every
transaction must obey the following rules:
·
A transaction T must issue the operation lock_item(X) before any read_item(X) or write_item(X) operations are performed
in T.
·
A transaction T must issue the operation unlock_item(X) after all read_item(X) and write_item(X) operations are completed
in T.
·
A transaction T will not issue a lock_item(X) operation if it already
holds the lock on item X.1
·
A transaction T will not issue an unlock_item(X) operation unless it
already holds the lock on item X.
These rules can be enforced by
the lock manager module of the DBMS. Between the lock_item(X) and unlock_item(X) operations in transaction T,
T is said to
hold the lock on item X. At most one transaction can hold the lock on a particular item. Thus no two transactions can access
the same item concurrently.
Shared/Exclusive (or
Read/Write) Locks. The preceding binary locking scheme is too restrictive for database items because at most, one
transaction can hold a lock on a given item. We should allow several
transactions to access the same item X
if they all access X for reading purposes only. This is because
read operations on the same item by different transactions are not conflicting
(see Section 21.4.1). However, if a transaction is to write an item X, it must have exclusive access to X. For this purpose, a different type of
lock called a multiple-mode lock is
used. In this scheme—called shared/exclusive
or read/write locks—there are three
locking operations: read_lock(X), write_lock(X), and unlock(X). A lock associated with an
item X, LOCK(X), now has three possible
states: read-locked, write-locked, or unlocked. A read-locked item is also called share-locked because other transactions are
allowed to read the item, whereas a write-locked
item is called exclusive-locked
because a single transaction exclusively holds the lock on the item.
One method for implementing the preceding operations on a read/write
lock is to keep track of the number of transactions that hold a shared (read)
lock on an item in the lock table. Each record in the lock table will have four
fields: <Data_item_name, LOCK,
No_of_reads, Locking_transaction(s)>. Again, to save space, the system needs to maintain lock records only for locked items in the lock table. The value
(state) of LOCK
is either read-locked or write-locked, suitably
coded (if we assume no records are kept in the lock table for
unlocked items). If LOCK(X)=write-locked, the value of locking_transaction(s) is a single
transaction that holds the exclusive (write) lock on X. If LOCK(X)=read-locked, the value of
locking transaction(s) is a list of one or more transactions that hold the
shared (read) lock on X. The three
operations read_lock(X), write_lock(X), and unlock(X) are described in Figure
22.2. As before,
each of the three locking operations should be
considered indivisible; no interleav-ing should be allowed once one of the
operations is started until either the opera-tion terminates by granting the
lock or the transaction is placed in a waiting queue for the item.
When we use the shared/exclusive locking scheme, the system must enforce
the fol-lowing rules:
A transaction T must issue the operation read_lock(X) or write_lock(X) before any read_item(X) operation is performed in T.
A transaction T must issue the operation write_lock(X) before any write_item(X) operation is performed in T.
read_lock(X):
if LOCK(X) = “unlocked”
then begin LOCK(X) ← “read-locked”; no_of_reads(X) ← 1
end
else if LOCK(X) = “read-locked”
then no_of_reads(X) ← no_of_reads(X)
+ 1 else begin
wait (until LOCK(X) = “unlocked”
and the lock manager wakes
up the transaction); go to B
end; write_lock(X):
if LOCK(X) = “unlocked”
then LOCK(X) ← “write-locked” else begin
wait (until LOCK(X) = “unlocked”
and the lock manager wakes
up the transaction); go to B
end;
unlock (X):
if LOCK(X) = “write-locked”
then begin LOCK(X) ← “unlocked”;
wakeup one of the waiting
transactions, if any
end
else it LOCK(X) = “read-locked”
then begin
no_of_reads(X) ← no_of_reads(X)
−1;
if no_of_reads(X) = 0
then
begin LOCK(X) = “unlocked”;
wakeup one of the waiting
transactions, if any
end shared-exclusive)
end;
Figure 22.2 Locking and unlocking operations for two-
mode (read-write or locks.
·
A transaction T must issue the operation unlock(X) after all read_item(X) and write_item(X) operations are completed
in T.3
·
A transaction T will not issue a read_lock(X) operation if it already
holds a read (shared) lock or a write (exclusive) lock on item X. This rule may be relaxed, as we
discuss shortly.
·
A transaction T will not issue a write_lock(X) operation if it already
holds a read (shared) lock or write (exclusive) lock on item X. This rule may also be relaxed, as we
discuss shortly.
·
A transaction T will not issue an unlock(X) operation unless it
already holds a read (shared) lock or a write (exclusive) lock on item X.
Conversion of Locks. Sometimes it is desirable to relax conditions 4 and 5 in the preceding list in order to allow lock
conversion; that is, a transaction that already holds a lock on item X is allowed under certain conditions to
convert the lock from one locked
state to another. For example, it is possible for a transaction T to issue a read_lock(X) and then later to upgrade the lock by issuing a write_lock(X) operation. If T is the only transaction holding a read lock on X at the time it issues the write_lock(X) operation, the lock can be
upgraded; otherwise, the transaction must wait. It
is also possible for a transaction T
to issue a write_lock(X) and then later to downgrade the lock by issuing a read_lock(X) operation. When upgrading and downgrading of locks is used, the lock
table must include transaction identifiers in the record structure for each
lock (in the locking_transaction(s) field) to store the information on which
transactions hold locks on the item. The descriptions of the read_lock(X) and write_lock(X) operations in Figure 22.2
must be changed appropri-ately to allow for lock upgrading and downgrading. We
leave this as an exercise for the reader.
Using
binary locks or read/write locks in transactions, as described earlier, does
not guarantee serializability of schedules on its own. Figure 22.3 shows an example
where the preceding locking rules are followed but a nonserializable schedule
may result. This is because in Figure 22.3(a) the items Y in T1 and X in T2
were unlocked too early. This allows a schedule such as the one shown in Figure
22.3(c) to occur, which is not a serializable schedule and hence gives
incorrect results. To guarantee serializability, we must follow an additional protocol concerning the
positioning of locking and unlocking operations in every transaction. The
best-known protocol, two-phase locking, is described in the next section.
2. Guaranteeing
Serializability by Two-Phase Locking
A transaction is said to follow the two-phase
locking protocol if all locking
operations (read_lock, write_lock) precede the first unlock
operation in the transaction. Such a transaction can be divided into two phases: an expanding or growing (first) phase,
during which new locks on items can be acquired but none can be released; and a shrinking (second) phase, during which existing locks can be released
but no new locks can be acquired. If lock conversion is allowed, then upgrading
of locks (from read-locked to write-locked) must be done during the expanding
phase, and downgrading of locks (from write-locked to read-locked) must be done
in the


shrinking phase. Hence, a read_lock(X) operation that downgrades an already
held write lock on X can appear only
in the shrinking phase.
Transactions
T1 and T2 in Figure 22.3(a) do not
follow the two-phase locking protocol because the write_lock(X) operation follows the unlock(Y) operation in T1, and similarly the write_lock(Y)
operation follows the unlock(X) operation in T2. If we enforce two-phase locking, the transactions
can be rewritten as T1 and
T2 , as shown in Figure
22.4. Now, the schedule shown in Figure 22.3(c) is not permitted for T1 and T2 (with their modified order of locking and unlocking
operations) under the rules of locking described in Section 22.1.1 because T1 will issue its write_lock(X) before
it
unlocks item Y; consequently, when T2 issues its read_lock(X), it is
forced to wait until T1
releases the lock by issuing an unlock (X) in the schedule.
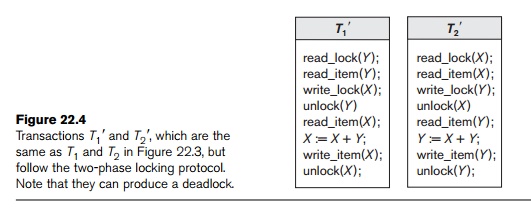
It can be proved that, if every
transaction in a schedule follows the two-phase locking protocol, the schedule
is guaranteed to be serializable,
obviating the need to test for serializability of schedules. The locking
protocol, by enforcing two-phase locking rules, also enforces serializability.
Two-phase locking may limit the amount of concurrency that can occur in
a schedule because a transaction T
may not be able to release an item X
after it is through using it if T
must lock an additional item Y later;
or conversely, T must lock the
additional item Y before it needs it
so that it can release X. Hence, X must remain locked by T until all items that the transaction
needs to read or write have been locked; only then can X be released by T.
Meanwhile, another transaction seeking to access X may be forced to wait, even though T is done with X;
conversely, if Y is locked earlier
than it is needed, another transaction seeking to access Y is forced to wait even though T
is not using Y yet. This is the price
for guaranteeing serializability of all schedules without having to check the
schedules themselves.
Although the two-phase locking protocol guarantees serializability (that
is, every schedule that is permitted is serializable), it does not permit all possible serializable schedules
(that is, some serializable schedules will be prohibited by the protocol).
Basic, Conservative,
Strict, and Rigorous Two-Phase Locking. There are
a number of variations of two-phase locking (2PL). The technique just
described is known as basic 2PL. A
variation known as conservative 2PL
(or static 2PL) requires a
transaction to lock all the items it accesses before the transaction begins execution,
by predeclaring its read-set and write-set. Recall from Section 21.1.2 that the read-set of a
transaction is the set of all items that the transaction reads, and the write-set is the set of all items that
it writes. If any of the predeclared items needed cannot be locked, the transaction does not lock any item; instead,
it waits until all the items are available for locking. Conservative 2PL is a
deadlock-free protocol, as we will see in Section 22.1.3 when we discuss the
deadlock problem. However, it is difficult to use in practice because of the
need to predeclare the read-set and write-set, which is not possible in many
situations.
In practice, the most popular variation of 2PL is strict 2PL, which guarantees strict schedules (see Section 21.4).
In this variation, a transaction T
does not release any of its exclusive (write) locks until after it commits or aborts. Hence, no other transaction can read
or write an item that is written by T
unless T has committed, leading to a
strict schedule for recoverability. Strict 2PL is not deadlock-free. A more
restrictive variation of strict 2PL is rigorous
2PL, which also guarantees strict schedules. In this variation, a
transaction T does not release any of
its locks (exclusive or shared) until after it commits or aborts, and so it is
easier to implement than strict 2PL. Notice the difference between conservative
and rigorous 2PL: the former must lock all its items before it starts, so once the transaction starts it is in its
shrinking phase; the latter does not unlock any of its items until after it terminates (by committing or
aborting), so the transaction is in its expanding phase until it ends.
In many cases, the concurrency
control subsystem itself is responsible for generating the read_lock and write_lock requests. For example, suppose the system is to enforce the strict 2PL
protocol. Then, whenever transaction T
issues a read_item(X), the system calls the read_lock(X) operation on behalf of T. If the state of LOCK(X) is write_locked by some
other transaction T , the system
places T in the waiting queue for
item X; otherwise, it grants the read_lock(X) request and permits the read_item(X) operation of T to execute. On the other hand, if transaction T issues a
write_item(X), the system calls the write_lock(X) operation on behalf of T. If the state of LOCK(X) is write_locked or read_locked by
some other transaction T , the system
places T in the waiting queue for
item X; if the state of LOCK(X) is read_locked and T itself is the only transaction holding
the read lock on X, the system
upgrades the lock to write_locked and
permits the write_item(X) operation by T. Finally, if the state of LOCK(X) is unlocked, the system
grants the write_lock(X) request and permits the write_item(X) operation to execute.
After each action, the system must update its lock table appropriately.
The use of locks can cause two additional problems: deadlock and
starvation. We discuss these problems and their solutions in the next section.
3. Dealing with
Deadlock and Starvation
Deadlock occurs when each transaction T
in a set of two or more transactions is waiting for some item that is locked
by some other transaction T in the
set. Hence, each transaction in the set is in a waiting queue, waiting for one
of the other trans-actions in the set to release the lock on an item. But
because the other transaction is also waiting, it will never release the lock.
A simple example is shown in Figure 22.5(a), where the two transactions T1 and T2 are deadlocked in a partial schedule; T1 is in the waiting queue for
X, which is locked by T2 , while T2 is in the
waiting queue for Y, which is locked by T1 . Meanwhile, neither T1 nor T2 nor any other transaction can access items X and Y.
Deadlock Prevention Protocols. One way
to prevent deadlock is to use a deadlock prevention protocol. One deadlock prevention protocol,
which is used

in
conservative two-phase locking, requires that every transaction lock all the items it needs in advance (which is generally not a practical
assumption)—if any of the items
cannot be obtained, none of the items are locked. Rather, the transaction waits
and then tries again to lock all the items it needs. Obviously this solution
further limits concurrency. A second protocol, which also limits concurrency,
involves ordering all the items in
the database and making sure that a transaction that needs several items will lock them according to that order. This
requires that the program-mer (or the system) is aware of the chosen order of
the items, which is also not practical in the database context.
A number
of other deadlock prevention schemes have been proposed that make a decision
about what to do with a transaction involved in a possible deadlock situation:
Should it be blocked and made to wait or should it be aborted, or should the
transaction preempt and abort another transaction? Some of these techniques use
the concept of transaction timestamp
TS(T), which is a unique identifier assigned to each transaction. The
timestamps are typically based on the order in which trans-actions are started;
hence, if transaction T1
starts before transaction T2,
then TS(T1) < TS(T2). Notice that the older transaction (which starts first)
has the smaller time-stamp value. Two
schemes that prevent deadlock are called wait-die
and wound-wait. Suppose that
transaction Ti tries to
lock an item X but is not able to
because X is locked by some other
transaction Tj with a
conflicting lock. The rules followed by these schemes are:
Wait-die.
If TS(Ti) < TS(Tj), then (Ti older than Tj) Ti is allowed to wait; otherwise (Ti younger than Tj)
abort Ti (Ti dies) and restart it later with
the same timestamp.
Wound-wait.
If TS(Ti) < TS(Tj), then (Ti older than Tj) abort Tj (Ti wounds Tj)
and restart it later with the same
timestamp; otherwise (Ti younger
than Tj) Ti is allowed to wait.
In
wait-die, an older transaction is allowed to wait for a younger transaction, whereas a younger transaction
requesting an item held by an older transaction is aborted and restarted. The
wound-wait approach does the opposite: A younger transaction is allowed to wait for an older one, whereas an older
transaction requesting an item held by a younger transaction preempts the younger transaction by
aborting it. Both schemes end up aborting the younger of the two transactions (the transaction that started
later) that may be involved in a
deadlock, assuming that this will waste less processing. It can be shown that
these two techniques are deadlock-free,
since in wait-die, transactions only wait for younger transactions so no cycle
is created. Similarly, in wound-wait, transactions only wait for older
transactions so no cycle is created. However, both techniques may cause some
transactions to be aborted and restarted needlessly, even though those
transactions may never actually cause a
deadlock.
Another
group of protocols that prevent deadlock do not require timestamps. These
include the no waiting (NW) and cautious waiting (CW) algorithms. In the no waiting
algorithm, if a transaction is unable to obtain a lock, it is immediately aborted and then restarted after a
certain time delay without checking whether a deadlock will actually occur or
not. In this case, no transaction ever waits, so no deadlock will occur.
However, this scheme can cause transactions to abort and restart needlessly.
The cautious waiting algorithm was
proposed to try to reduce the number of needless aborts/restarts. Suppose that
transaction Ti tries to
lock an item X but is not able to do
so because X is locked by some other
transaction Tj with a conflicting lock. The cautious waiting
rules are as follows:
Cautious
waiting. If Tj is not
blocked (not waiting for some other locked
item), then Ti is
blocked and allowed to wait; otherwise abort Ti.
It can be
shown that cautious waiting is deadlock-free, because no transaction will ever
wait for another blocked transaction. By considering the time b(T)
at which each blocked transaction T
was blocked, if the two transactions Ti
and Tj above both become
blocked, and Ti is waiting
for Tj, then b(Ti)
< b(Tj), since Ti
can only wait for Tj at a
time when T j is not blocked itself. Hence, the blocking times form
a total ordering on all blocked transactions, so no cycle that causes deadlock
can occur.
Deadlock Detection. A second,
more practical approach to dealing with deadlock is deadlock detection, where the system
checks if a state of deadlock actually exists. This solution is attractive if
we know there will be little interference among the transactions—that is, if
different transactions will rarely access the same items at the same time. This
can happen if the transactions are short and each transaction locks only a few
items, or if the transaction load is light. On the other hand, if transactions
are long and each transaction uses many items, or if the transaction load is
quite heavy, it may be advantageous to use a deadlock prevention scheme.
A simple
way to detect a state of deadlock is for the system to construct and maintain
a wait-for graph. One node is
created in the wait-for graph for each transaction that is currently executing.
Whenever a transaction Ti
is waiting to lock an item X that is
currently locked by a transaction Tj,
a directed edge (Ti → Tj) is created in the wait-for graph. When Tj releases the lock(s) on
the items that Ti was
waiting for, the directed edge is dropped from the wait-for graph. We have a
state of dead-lock if and only if the wait-for graph has a cycle. One problem
with this approach is the matter of determining when the system should check for a deadlock. One possibility is to
check for a cycle every time an edge is added to the wait-for graph, but this
may cause excessive overhead. Criteria such as the number of currently
executing transactions or the period of time several transactions have been
waiting to lock items may be used instead to check for a cycle. Figure 22.5(b)
shows the wait-for graph for the (partial) schedule shown in Figure 22.5(a).
If the
system is in a state of deadlock, some of the transactions causing the deadlock
must be aborted. Choosing which transactions to abort is known as victim selection. The algorithm for
victim selection should generally avoid selecting transactions that have been
running for a long time and that have performed many updates, and it should try
instead to select transactions that have not made many changes (younger
transactions).
Timeouts. Another simple scheme to deal
with deadlock is the use of timeouts. This
method is practical because of its low overhead and simplicity. In this method,
if a transaction waits for a period longer than a system-defined timeout
period, the system assumes that the transaction may be deadlocked and aborts
it—regardless of whether a deadlock actually exists or not.
Starvation. Another problem that may occur
when we use locking is starvation, which
occurs when a transaction cannot proceed for an indefinite period of time while
other transactions in the system continue normally. This may occur if the
waiting scheme for locked items is unfair, giving priority to some transactions
over others. One solution for starvation is to have a fair waiting scheme, such
as using a first-come-first-served queue;
transactions are enabled to lock an item in the order in which they originally requested the lock. Another scheme allows
some transactions to have priority over others but increases the priority of a
transaction the longer it waits, until it eventually gets the highest priority
and proceeds. Starvation can also occur because of victim selection if the
algorithm selects the same transaction as victim repeatedly, thus causing it
to abort and never finish execution. The algorithm can use higher priorities
for transactions that have been aborted multiple times to avoid this problem.
The wait-die and wound-wait schemes discussed previously avoid starvation,
because they restart a transaction that has been aborted with its same original
timestamp, so the possibility that the same transaction is aborted repeatedly
is slim.
Related Topics