Differential and Linear Cryptanalysis

DIFFERENTIAL AND LINEAR CRYPTANALYSIS

For  most of its life, the prime concern with DES has been its vulnerability   to brute-force attack because of its relatively short (56 bits) key length. However, there has also been interest in  finding cryptanalytic attacks on  DES. With the increasing popularity of block ciphers with longer key lengths, including triple DES, brute-force attacks have become increasingly impractical. Thus, there has been increased emphasis on cryptanalytic attacks on DES and other symmetric block ciphers. In this section, we provide a brief overview of the two most powerful and promising approaches: differential cryptanalysis and linear cryptanalysis.

Differential Cryptanalysis

One of the most significant advances in cryptanalysis in recent years is differential cryptanalysis. In this section, we discuss the technique and its applicability to DES.

HISTORY Differential cryptanalysis was not reported in the open literature until 1990. The first published effort appears to have been the cryptanalysis of a block cipher called FEAL by Murphy [MURP90]. This was followed by a number of papers by Biham and Shamir, who demonstrated this form of attack on a variety of encryption algorithms and hash functions; their results are summarized in [BIHA93].

The most publicized results for this approach have been those that have application to DES. Differential cryptanalysis is the first published attack that is capable of breaking DES in less than 255 encryptions. The scheme, as reported in [BIHA93], can successfully cryptanalyze DES with an effort on the order of 247 encryptions, requiring 247 chosen plaintexts. Although 247 is certainly significantly less than 255, the need for the adversary to find 247 chosen plaintexts makes this  attack  of  only  theoretical interest.

Although differential cryptanalysis is a powerful tool, it does not do very well against DES. The reason, according to a member of the IBM team that designed DES [COPP94], is that differential cryptanalysis was known to the team as early as 1974. The need to strengthen DES against attacks using differential cryptanalysis played a large part in the design of the S-boxes and the permutation P. As evidence of the impact of these changes, consider these comparable results reported in [BIHA93]. Differential cryptanalysis of an eight-round LUCIFER algorithm requires only 256 chosen plaintexts, whereas an attack on an eight-round version of DES requires 214 chosen plaintexts.

DIFFERENTIAL CRYPTANALYSIS ATTACK The differential cryptanalysis attack is complex; [BIHA93] provides a complete description. The rationale behind differential cryptanalysis is to observe the behavior of pairs of text blocks evolving along each round of the cipher, instead of observing the evolution of a single text block. Here, we provide a brief overview so that you can get the flavor of the attack.

We begin with a change in notation for DES. Consider the original plaintext block m to consist of two halves m0, m1. Each round of DES maps the right-hand input into the left-hand output and sets the right-hand output to be a function of the left-hand input and the subkey for this round. So, at each round, only one new 32-bit block is created. If we label each new block mi (2 … i … 17), then the intermediate message halves are related as follows:

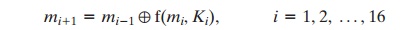
In differential cryptanalysis, we start with two messages, m and m¿, with a known XOR difference  Δm  =  m  NOR  m¿, and consider the difference between the intermediate message halves: Δmi  =  mi NOR m¿i. Then we have

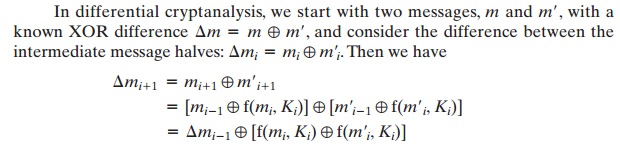
Now, suppose that many pairs of inputs to f with the same difference yield the same output difference if the same subkey is used. To put this more precisely, let us say that X may cause Y with probability p, if for a fraction p of the pairs in which the input XOR is X, the output XOR equals Y. We want to suppose that there are a number of values of X that have high probability of causing a particular output difference. Therefore, if we know ¢mi - 1 and ¢mi with high probability, then we know ¢mi + 1 with high probability. Furthermore, if a number of such differences are determined, it is feasible to determine the subkey used in the function f.

The overall strategy of differential cryptanalysis is based on these considerations for a single round. The procedure is to begin with two plaintext messages m and m¿ with a given difference and trace through a probable pattern of differences after each round to yield a probable difference for the ciphertext. Actually, there are two proba- ble patterns of differences for the two 32-bit halves: (¢m17 || ¢m16). Next, we submit m and m¿ for encryption to determine the actual difference under the unknown key and compare the result to the probable difference. If there is a match,

then we suspect that all the probable patterns at all the intermediate rounds are correct. With that assumption, we can make some deductions about the key bits. This procedure must be repeated many times to determine all the key bits.

Figure 3.8, based on a figure in [BIHA93], illustrates the propagation of differ- ences through three rounds of DES. The probabilities shown on the right refer to the probability that a given set of intermediate differences will appear as a function

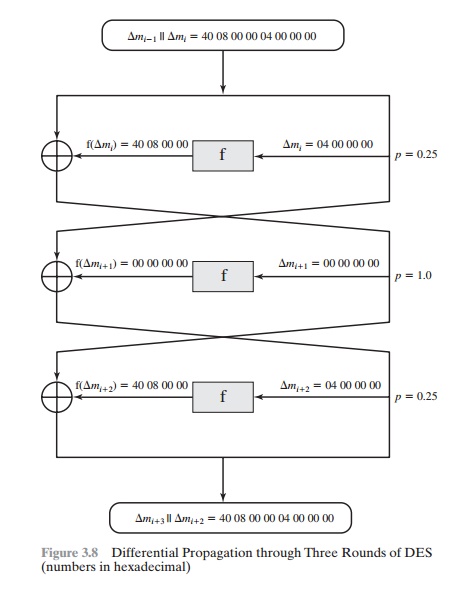
of the input differences. Overall, after three rounds, the probability that the output difference is as shown is equal to 0.25 * 1 * 0.25 = 0.0625.

Linear Cryptanalysis

A more recent development is linear cryptanalysis, described in [MATS93]. This attack is based on finding linear approximations to describe the transformations performed in DES. This method can find a DES key given 243 known plaintexts, as compared to 247 chosen plaintexts for differential cryptanalysis. Although this is a minor improvement, because it may be easier to acquire known plaintext rather than chosen plaintext, it still leaves linear cryptanalysis infeasible as an attack on DES. So far, little work has been done by other groups to validate the linear cryptanalytic approach.

We now give a brief summary of the principle on which linear cryptanalysis is based. For a cipher with n-bit plaintext and ciphertext blocks and an m-bit key, let

(where x = 0 or 1; 1 <= a; b <= n; c <= m; and where the a, b, and g terms represent fixed, unique bit locations) that holds with probability p != 0.5. The further p is from 0.5, the more effective the equation. Once a proposed relation is determined, the pro- cedure is to compute the results of the left-hand side of the preceding equation for a large number of plaintext–ciphertext pairs. If the result is 0 more than half the time, assume K[g1, g2, ….. , gc]  = 0. If it is 1 most of the time, assume K[g1, g2, ….. , gc]  = 1. This gives us a linear equation on the key bits.Try to get more such relations so that we can solve for the key bits. Because we are dealing with linear equations, the problem can be approached one round of the cipher at a time, with the results  combined.