Application of the Momentum equation for Rapidly Varied Flow

Application of the Momentum equation for Rapidly Varied Flow

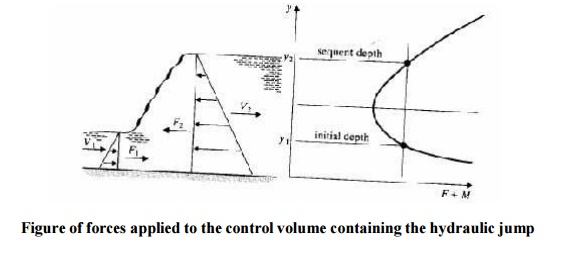
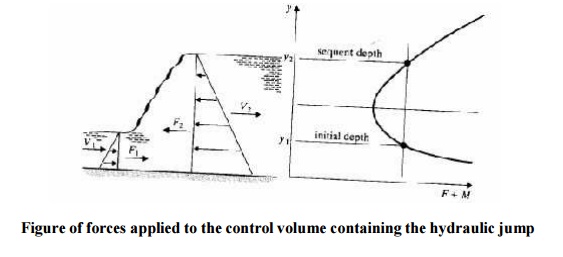
The hydraulic jump is an important feature in open channel flow and is an example of rapidly varied flow. A hydraulic jump occurs when a super-critical flow and a sub-critical flow meet. The jump is the mechanism for the to surface to join. They join in an extremely turbulent manner which causes large energy losses.

Because of the large energy losses the energy or specific energy equation cannot be use in analysis, the momentum equation is used instead.

Resultant force in x- direction = F₁ - F₂

Momentum change = M₂ - M₁

F₁ - F₂ = M₂ - M₁

Or for a constant discharge

F₁ - F₂ = M₂ - M₁ = constant

For a rectangular channel this may be evaluated using

So knowing the discharge and either one of the depths on the upstream or downstream side of the jump the other - or conjugate depth - may be easily computed.

More manipulation with Equation and the specific energy give the energy loss in the jump as

Del E = (y₂-y₁)³ / Del(y₁y₂)

These are useful results and which can be used in gradually varied flow calculations to determine water surface profiles.

In summary, a hydraulic jump will only occur if the upstream flow is super-critical. The higher the upstream Froude number the higher the jump and the greater the loss of energy in the jump.