Zero moment point method

Zero moment point method

A one bay multi-storey framed building of height h and width l is considered. Assume the building is subjected to lateral loads as a result of ground motion. The bending moment diagram due to lateral loading is shown in Fig. 20.1.

The position of the point where the moment is zero is defined as the zero moment point (ZMP).

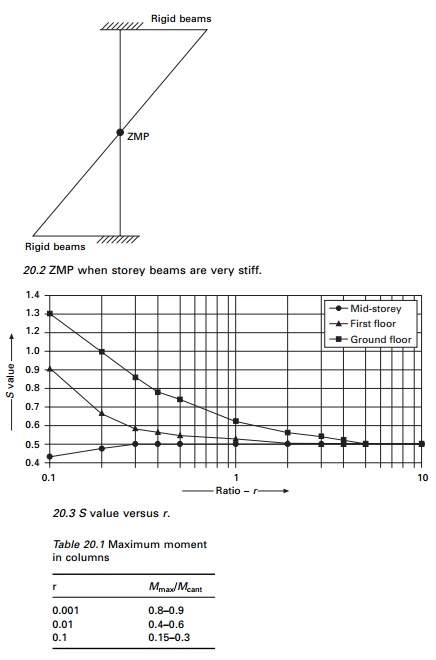
If storey beams are very stiff, the ZMP lies at the mid-height of each storey and if the beams are very flexible, the behaviour is more like a cantilever (see Fig. 20.2).

The approximate position of ZMP will now be determined for uniform and non-uniform frames.

1  Uniform frames

It is assumed that storey heights are constant and moments of inertia are constant at each storey. The frame is analysed for inverted triangular load. Various analyses have been performed with different values of beam to column stiffness as r = 0.01, 0.1, 0.5, 1, 2, 5, 10, 10 000. The positions of ZMP are as follows. The average values of S is plotted for various values of r for ground storey, first floor and mid-height of the building in Fig. 20.3.

•       At first storey S is 0.5–0.6 for r > 2 and greater than 1 for r < 0.2 (ground).

•       At mid-heights S is about 0.5 for r > 0.5 average values of S at ground floor, first floor and new mid-height floor are shown in Fig. 20.3.

It is to advisable to increase the moments at mid-height by 10–20% with respect to moments based on S_m. By relating maximum moment on columns

(M_max) to that, acting on cantilever (M_cant) the ratio of (M_max/M_cant) as shown in Table 20.1 are obtained.

2     Non-uniform frames

When the frame has a varying column moment of inertia but constant beam moment of inertia, the frame can be analysed using the curves for uniform moment of inertia as

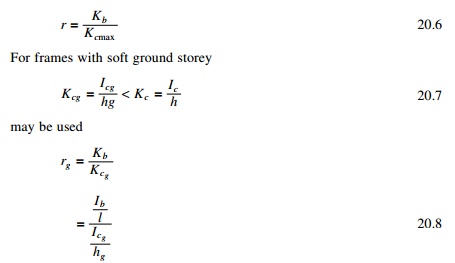
3  Substitution in equivalent frame method

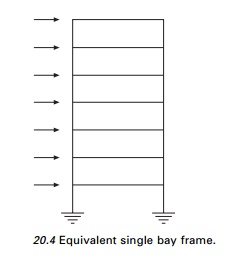
A multi-storey multi-bay frame is replaced by the equivalent single bay frame shown in Fig. 20.4.

Studies show the deflection of the substitution frame is identical to the actual frame. The bending moment in columns of the substitution frame is

The distribution is accurate only if the beams are very stiff (r > 10) or very flexible (r < 0.05). Hence computed moments in interior columns have to be multiplied by the factors as

•       for ground floor – 1.1 to 1.2

•       for other floors – 1.2 to 1.3

Using equilibrium equations beam moment may be calculated.

4  Deflection estimation

The deformed shape of one bay, multi-storey structure depends on the ratio of stiffness of beam to column r = k_b/k_c and on the type of loading 0.1 < r < 5. The deformed shape is close to a straight line as advocated by most seismic codes. The deflections are sensitive to changes in geometry and rigidity and so only the order of magnitude can be estimated. When 2 < r < 5. it is strong beam–weak column design and 0.01 < r < 1 is the weak beam and strong column design which is preferred for earthquake design.

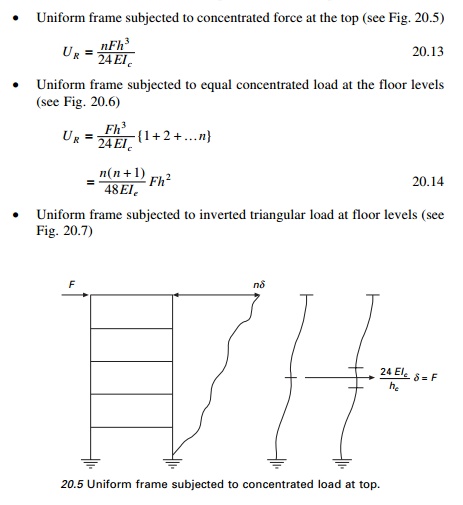
Uniform frame subjected to concentrated force at the top (see Fig. 20.5)

Uniform frame subjected to equal concentrated load at the floor levels (see Fig. 20.6)

Uniform frame subjected to inverted triangular load at floor levels (see Fig. 20.7)

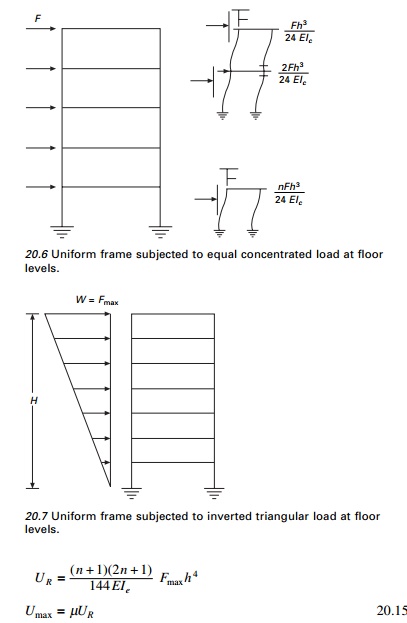
The average value of µ is shown in Fig. 20.11 which may be used for any lateral load distribution.

For high values of beam stiffness (weak columns and strong beam) (r >> 1) the frame deforms as shown in Fig. 20.8. For low values of beam stiffness (strong columns and weak beam) r < 0.1 the frame behaves like of cantilever shown in Fig. 20.9.

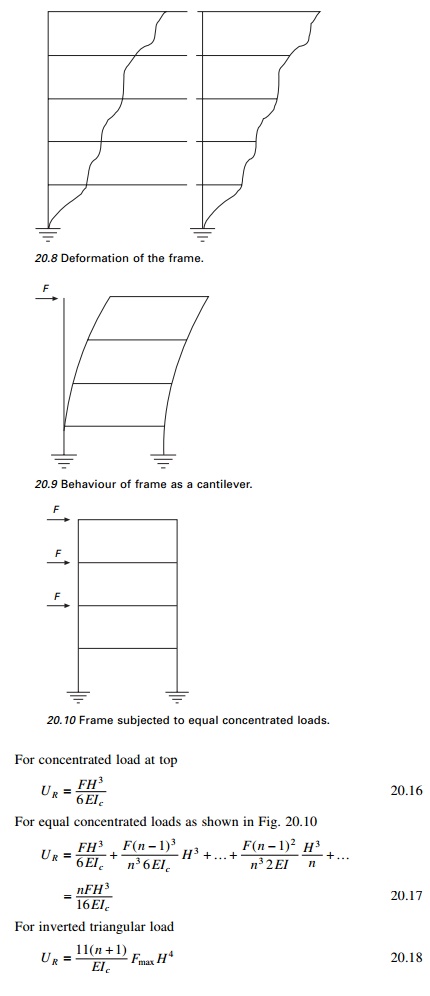
The deflection calculations are required for checking storey drafts.

For regular frames, since the deflection shape is a straight line, the following relation holds good (see Fig. 20.11).

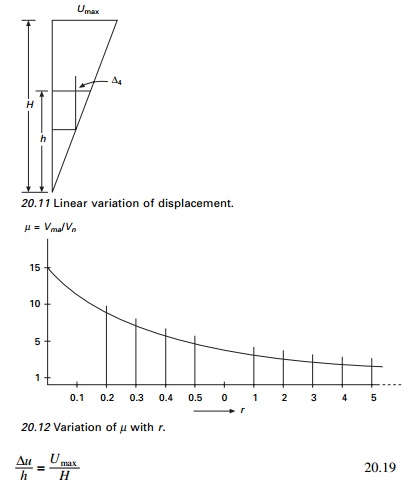
For buildings with the height of the ground floor (h_g) > height of floors above h is (h_g > h)

where S_G can be taken from graph (Fig. 20.3).