Weighted Residual Method

WEIGHTED RESIDUAL METHOD

It is a powerful approximate procedure applicable to several problems. For non –structural problems, the method of weighted residuals becomes very useful. It has many types. The popular four methods are,

1. Point collocation method,

Residuals are set to zero at n different locations Xi, and the weighting function wi is denoted as d(x - xi).

roblem I

Find the solution for the following differential equation.

Problem 2

The differential equation of a physical phenomenon is given by

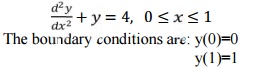
Obtain one term approximate solution by using galerkin method Solution:

Here the boundary conditions are not homogeneous so we assume a trial function as, y=a1x(x-1)+x

first we have to verify whether the trial function satisfies the boundary condition or not y=a1x(x-1)+x

when x=0, y=0 x=1, y=1

Resuldual R:

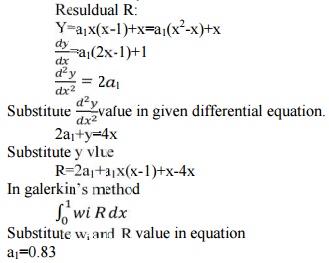
So one of the approximate solution is,

y= 0.83x(x-1)+x = 0.83x2-0.83x+x

y=0.83 x2+0.17x

Problem 3

Find the deflection at the center of a simply supported beam of span length l subjected to uniform distributed load throughout its length as shown using (a) point collection method (b) Sub-

domain method    (c)least squared and (d) galerkin’n method.        

Solution:

THE GENERAL WEIGHTED RESIDUAL STATEMENT

After understanding the basic techniques and successfully solved a few pro blem general weighted residual statement can b e written as

R dx=0 for i= 1,2,…..n

Where w_i=N_i

The better result will be obtained by considering more terms in polynomial and trigonometric series.