Chapter: 11th 12th std standard Class Physics sciense Higher secondary school College Notes
Superposition principle of waves
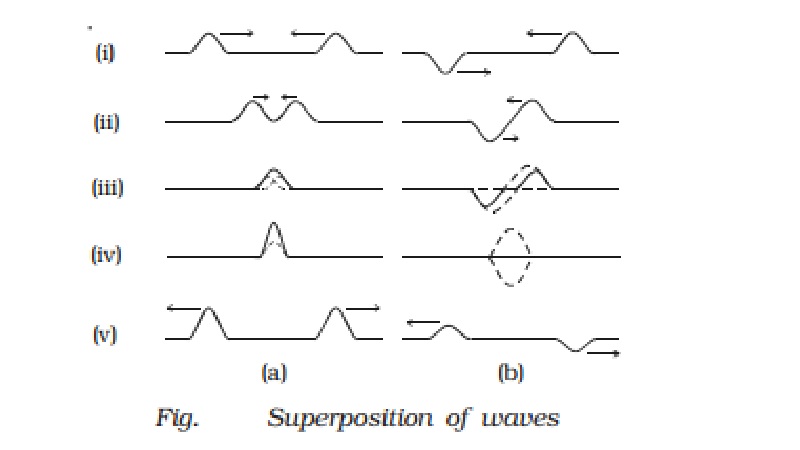
Superposition principle
When two waves travel in a medium
simultaneously in such a way that each wave represents its separate motion,
then the resultant displacement at any point at any time is equal to the vector
sum of the individual displacements of the waves.
This principle is
illustrated by means of a slinky in the Fig. (a).
1. In the figure, (i)
shows that the two pulses pass each other,
2. In the figure, (ii)
shows that they are at some distance apart
3.
In the figure, (iii) shows that they overlap partly
4.
In the figure, (iv) shows that resultant is maximum
Fig.
b illustrates the same events but with pulses that are equal and opposite.
If Vector Y1 JG and Vector Y2 JJG are the
displacements at a point, then the resultant displacement is given by
Vector Y = Vector Y1 + Vector Y2.
If
| Vector Y2| - | Vector Y2|
= a , and if the two waves have their
displacements in the same direction, then | Vector Y | = a + a = 2a
If the two waves have their displacements in
the opposite direction, then | Vector Y | = a + (-a) = 0
The
principle of superposition of waves is applied in wave phenomena such as
interference, beats and stationary waves.
Related Topics