Standing waves in strings - Sonometer

Standing waves in strings

In musical instruments like sitar, violin, etc. sound is produced due to the vibrations of the stretched strings. Here, we shall discuss the different modes of vibrations of a string which is rigidly fixed at both ends.

When a string under tension is set into vibration, a transverse progressive wave moves towards the end of the wire and gets reflected. Thus stationary waves are formed.

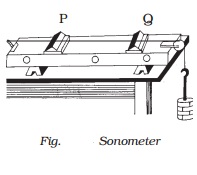
Sonometer

The sonometer consists of a hollow sounding box about a metre long. One end of a thin metallic wire of uniform cross-section is fixed to a hook and the other end is passed over a pulley and attached to a weight hanger as shown in Fig.. The wire is stretched over two knife edges P and Q by adding sufficient weights on the hanger. The distance between the two knife edges can be adjusted to change the vibrating length of the wire.

A transverse stationary wave is set up in the wire. Since the ends are fixed, nodes are formed at P and Q and antinode is formed in the middle.

The length of the vibrating segment is l = λ/2

∴ λ = 2l. If n is the frequency of vibrating segment, then n = v/ λ =  v /2l

We know that v = root(T/m) where T is the tension and m is the mass per unit length of the wire.

N=1/2l.root(T/m)

Modes of vibration of stretched string

(i) Fundamental frequency

If a wire is stretched between two points, a transverse wave travels along the wire and is reflected at the fixed end. A transverse stationary wave is thus formed as shown in Fig..

When a wire AB of length l is made to vibrate in one segment then l = λ₁/2 .

∴ λ1 = 2l. This gives the lowest frequency called fundamental frequency n1=v/λ₁.

n₁ = 1/2l.root(T/m) ?????.(3)

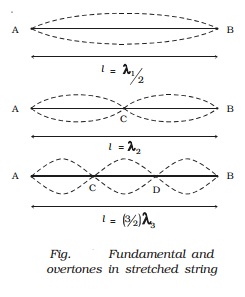
(ii) Overtones in stretched string

If the wire AB is made to vibrate in two segments then l = λ₂/2 +  λ₂/2

λ₂ = l.

But,n₂ = v/ λ₂

n₂ = 2n₁

n₂ is the frequency of the first overtone.

Since the frequency is equal to twice the fundamental, it is also known as second harmonic.

Similarly, higher overtones are produced, if the wire vibrates with more segments. If there are P segments, the length of each segment is

l/p = λ_p/2

or

λ_p = 2l/P

Frequency n_P = P/2l. root[T/m]

=Pn₁

(i.e) P^th harmonic corresponds to (P?1)^th overtone.

 Laws of transverse vibrations of stretched strings

The laws of transverse vibrations of stretched strings are (i) the law of length (ii) law of tension and (iii) the law of mass.

(i) For a given wire (m is constant), when T is constant, the fundamental frequency of vibration is inversely proportional to the vibrating length (i.e)

n α 1/l

or

 nl = constant.

(ii) For constant l and m, the fundamental frequency is directly proportional to the square root of the tension (i.e) n α root[T].

(iii) For constant l and T, the fundamental frequency varies inversely as the square root of the mass per unit length of the wire (i.e) n α 1/ root[m].