Square Root of Polynomials

Square Root of Polynomials

The square root of a given positive real number is another number which when multiplied with itself is the given number.

Similarly, the square root of a given expression p(x) is another expression q(x) which when multiplied by itself gives p(x), that is, q (x). q ( x ) = p(x)

So, |q (x)| = √p(x) where |q (x)|  is the absolute value of q(x).

The following two methods are used to find the square root of a given expression

(i) Factorization method

(ii) Division method

Progress Check

1. Is x 2 + 4x + 4 a perfect square?

2. What is the value of x in 3√x = 9 ?

3. The square root of 361x ⁴y² is _______.

4. √[ a²x² + 2abx + b²] = _________

5. If a polynomial is a perfect square then, its factors will be repeated  number of times (odd / even)

Find the Square Root by Factorization Method

Example 3.19

Find the square root of the following expressions

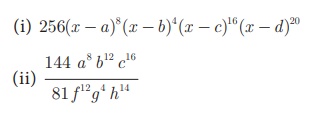
Solution

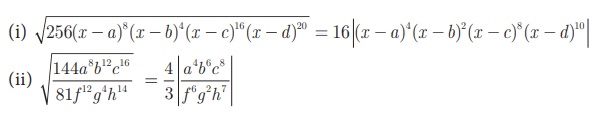
Example 3.20

Find the square root of the following expressions

(i) 16x ² + 9y ² − 24xy + 24x −18y + 9

(ii) (6x ² + x −1)(3x ² + 2x −1)(2x ² + 3x + 1)

(iii) [√15x² + (√3 + √10 ) x + √2][ √5x² + (2√5 + 1)x+2][( √3x² + (√2 + 2√3 ) x + 2√2]

Solution