Definition, Illustration, Example, Solution | Mathematics - Special cases of function | 10th Mathematics : UNIT 1 : Relation and Function
Chapter: 10th Mathematics : UNIT 1 : Relation and Function
Special cases of function
Special cases of function
There are some special
cases of a function which will be very useful. We discuss some of them below
(i) Constant function
(ii) Identity function
(iii) Real – valued
function
(i) Constant function
A function f : A
→ B is called a constant function if the range of f contains only one element.
That is, f (x ) = c , for all x ∈ A and for some fixed c ∈ B.
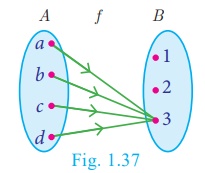
Illustration 16
From Fig.1.37, A =
{a,b,c,d} and B = {1, 2, 3} and f
= {(a, 3),(b, 3),(c,
3),(d, 3)} . Since, f (x) = 3 for every x ∈ A ,
Range of f = {3} , f
is a constant function.
(ii) Identity function
Let A be
a non–empty set. Then the function f: A → A defined by f (x) = x for all x ∈ A is called an identity function on A and is denoted by IA.
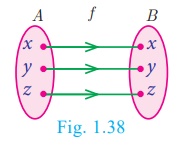
Illustration 17
If A = {a,b,c}
then f=IA = {(a,a),(b,b),(c,c)}
is an identity function on A.
(iii) Real valued function
A function f: A → B is called a real valued function if the range of f is a subset of the set of all real numbers R . That is, f (A) ⊆ R.
Example 1.17
Let f be a function from R to R defined by f (x) = 3x − 5 . Find the
values of a and b given that (a, 4) and (1, b)
belong to f.
Solution f (x) = 3x –
5 can be written as f = {(x,
3x – 5) | x ∈ R}
(a, 4) means
the image of a is 4. That is, f (a) = 4
3a – 5 = 4 ⇒ a = 3
(1, b) means
the image of 1 is b.
That is, f (1)
= b ⇒ b = −2
3(1) – 5 = b Þ b = –2
Example 1.18 The distance S (in
kms) travelled by a particle in time ‘t’ hours is given by S(t) = [ t2 + t ]/2. Find the distance
travelled by the particle after
(i) three and half
hours.
(ii) eight hours and
fifteen minutes.
Solution The distance travelled
by the particle in time t hours is given by 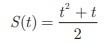
(i) t = 3.5 hours. Therefore 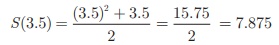
The distance travelled
in 3.5 hours is 7.875 kms.
t = 8.25 hours.
Therefore 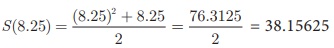
The distance travelled
in 8.25 hours is 38.16 kms, approximately.
Example 1.19
If the function f :
R → R is defined by 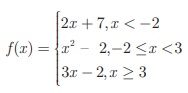 ,
,
then find the values
of
(i) f (4)
(ii) f (-2)
(iii) f (4) + 2f
(1)
(iii) [f (1) + 3f (4)] / f (-3)
Solution
The function f is
defined by three values in intervals I, II, III as shown by the side

For a given value of x
= a , find out the interval at which the point a is located,
there after find f (a) using the particular value defined in that
interval.
(i) First, we see
that, x = 4 lie in the third interval.
Therefore, f (x)
= 3x − 2 ; f (4) = 3(4) – 2 = 10
(ii) x = −2 lies in the second interval.
Therefore, f (x)
= x2 – 2 ; f (−2) = (−2)2 – 2 = 2
(iii) From (i), f (4)
= 10 .
To find f (1),
first we see that x = 1 lies in the second interval.
Therefore, f (x)
= x2 – 2 ⇒ f (1) = 12
– 2 = −1
So, f (4) + 2f
(1) = 10 + 2(−1) = 8
(iv) We know that f
(1) = -1 and f (4) = 10.
For finding f
(-3), we see that x = −3 , lies in the first interval.
Therefore, f (x)
= 2x + 7 ; thus, f (−3) = 2(−3) + 7 = 1
Hence 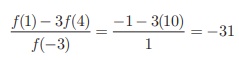
Related Topics