Chapter: Physics : Conducting Materials
Solved Problems: Conducting Materials
SOLVED PROBLEMS
1.The following datas are given for copper
Density = 8.92 × 103 kgm–3
Resistivity = 1.73 × 108 m
iii)Atomic weight = 63.5 kg
Calculate the mobility and the average time
collision of electrons in copper obeying classical laws

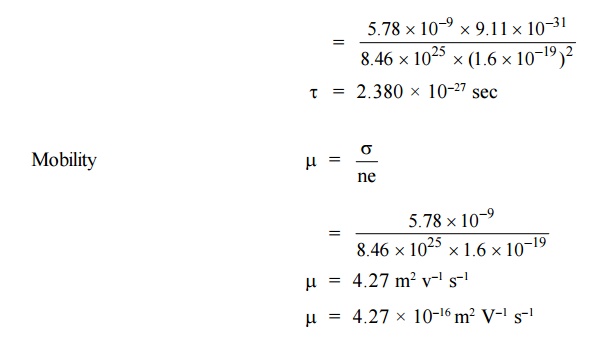
2.A uniform silver wire has a resistivity of
1.54×10–8 m at room temperature. For an electric field along the
wire of 1 volt cm–1, compute the average drift velocity of electron
assuming that there is 5.8 × 1028 conduction electrons /m3.
Also calculate the mobility.

3.The density of silver 10.5 × 103
kg–3 assuming that each silver atom provides one conduction
electron. The conductivity of silver at 20°C is 6.8 × 107 –1 m–1.
Calculate the density and mobility of electron in silver with atomic weight
107.9 × 10–3 kg m–2.

4.Calculate the drift velocity of electrons in
copper and current density in wire of diameter 0.16 cm which carries a steady
current of 10 A. Given n = 8.46 × 1028 m–3.
Solution:
Given:
Diameter of the wire d = 0.16 cm
Current flowing = 10 A

5. The resistivity of a piece of silver at room
temperature 1.6 × 10–8 m. The effective number of conduction
electrons is 0.9 per atom and the Fermi energy is 5.5 eV. Estimate the mean
free path of the conduction electrons. Calculate the electronic relaxation time
and the electronic drift velocity in a field of 100 Vm–1. The
density of silver is 1.05 × 104 kgm–3 (m/m* = 1).


6. A conducting rod contains 8.5 × 1028
electrons/m3. Calculate its resistivity at room temperature and also
the mobility of electrons if the collision time for electron scattering is 2 ×
10–14 sec.

7. valuate the Fermi function for energy KBT
above the Fermi energy.

8. Free electron density of aluminum is 18.1 × 1028 m–3.
Calculate its Calculate its Fermi energy at 0 K. [Planck’s constant and
mass of free electron are 6.62 × 10–34Js, and 9.1 × 10–34Kg]

9. The Fermi temperature of a metal is 24600 K. Calculate the Fermi
velocity.

10. Use the Fermi distribution function to
obtain the value of F(E) for E – EF = 0.01 eV at 200K.
Solution:
Given
data:

11. Calculate the drift velocity of the free
electrons (with a mobility of 3.5 × 10–3 m2 V–1
s–1) in copper for an electric field strength of 0.5 V m–1.

12. Copper has electrical conductivity at 300 K
as 6.40 × 107 m–1. Calculate the thermal conductivity of
copper.(Lorentz number is 2.44 × 10–8 W k–2).

13.The thermal and electrical conductivities of
copper at 20°C are 380 Wm–1 K–1 and 5.67 × 107 –1
m–1 respectively. Calculate the Lorentz number.


15. Calculate the Fermi energy of copper at 0 K
if the concentration of electron is 8.5 × 1028 m–3.

16. The mobility of electrons in copper 3×103m2V–1s–1
assuming e=1.6×10–19C and me=9.1×10–31 kg.
Calculate the mean collision time.
Solution:

17. The thermal conductivity of a metal is
123.92 Wm–1K–1. Find the electrical conductivity and
Lorentz number when the metal posses relaxation time 10–14 sec at
300 K. (Density of electron = 6×1028 per m3)

18. Calculate the drift velocity of the free
electrons in copper for electric field strength of 2Vm–1. (Mobility
of electrons µ = 3.5 × 10–3 m2V–1s–1).

19. Find the velocity of copper wire whose
cross-sectional area is 1 mm when the wire carries a current of 10 A. Assume
that each copper atom contributes one election to the electron gas.

ASSIGNMENT PROBLEMS
A Copper wire whose is 0.16 cm carries a steady current of 20 A.
What is the current density of wire? Also calculate the drift velocity of the
electrons in copper. (Ans : J = 9.952
A/m2 , and Vd = 7.35 x 10- 4 ms-1)
The thermal and electrical conductivities of Cu at 20°C are 390
Wm 1 K 1and 5.87 × 10–7 –1 m–1respectively.
Calculate the Lorentz number. (Ans :
2.267 × 10–8 W K–1)
Calculate the electrical and thermal conductivities of a metal rod
with relaxation time 10 14 second at 300K. Also calculate
the Lorentz number.
(Density
of electron = 6 × 1028 m–3)(Ans : = 1.6879 × 10–7 –1 m–1 , K =
123.927 Wm–1 K –1
, = 2.4474 × 10–18 W K–2)
Calculate the drift velocity and mean free path of copper when it
carries a steady current of 10 amperes and whose radius is 0.08 cm. Assume that
the mean thermal velocity 1.6 × 106 m/s and the resistivity of
copper 2 × 10–8 m.
(Ans :
(i) 36.6 x 10-5m/s (ii) 3.94 x 108m)
The resistivity of aluminum at room temperature is 2 × 10–8
m.Calculate i) The drift velocity ii) mean free path on the basis of classical
free electron theory.
(Ans :
(i) 0.396 ms-1; (ii) 2.65nm)
6. Using the Fermi function, evaluate the
temperature at which there is 1% probability in a solid will have an energy 0.5
eV above EF of 5 eV. (Ans :
1260 K)
Related Topics