Shortest-Route Algorithms

Shortest-Route Algorithms

This section presents two algorithms for solving both cyclic (i.e., containing loops) and acyclic networks:

1.  Dijkstra's algorithm

2.  Floyd's algorithm

Dijkstra's algorithm is designed to determine the shortest routes between the source node and every other node in the network. Floyd's algorithm is more general because it allows the determination of the shortest route between any two nodes in the network.

Dijkstra's Algorithm. Let u_i be the shortest distance from source node 1 to node i, and define d_ij (≥0) as the length of arc (i, j). Then the algorithm defines the label for an immediately succeeding node j as

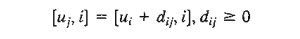
The label for the starting node is [0, --], indicating that the node has no predecessor. Node labels in Dijkstra's algorithm are of two types: temporary and permanent. A temporary label is modified if a shorter route to a node can be found. If no better route can be found, the status of the temporary label is changed to permanent.

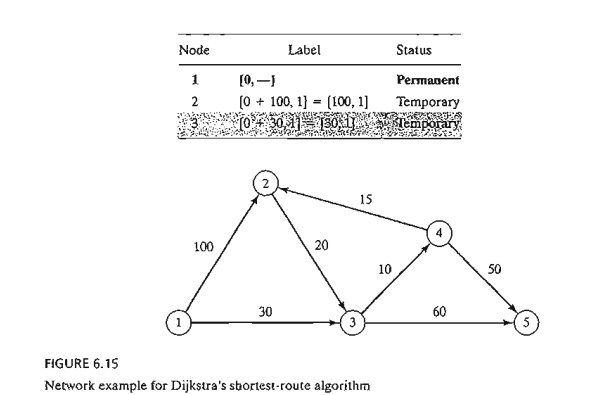
Example 6.3-4

The network in Figure 6.15 gives the permissible routes and their lengths in miles between city 1 (node 1) and four other cities (nodes 2 to 5). Determine the shortest routes between city 1 and each of the remaining four cities.

Iteration 0.         Assign the permanent label [0, -- ] to node 1.

Iteration 1. Nodes 2 and 3 can be reached from (the last permanently labeled) node 1. Thus, the list of labeled nodes (temporary and permanent) becomes

For the two temporary labels [100, 1] and [30, 1], node 3 yields the smaller distance (u₃ = 30). Thus, the status of node 3 is changed to permanent.

Iteration 2. Nodes 4 and 5 can be reached from node 3, and the list of labeled nodes becomes

The status of the temporary label [40,3] at node 4 is changed to permanent (u₄ = 40).

Iteration 3. Nodes 2 and 5 can be reached from node 4. Thus, the list of labeled nodes is updated as

Node 2's temporary label [100, 1] obtained in iteration 1 is changed to [55,4) in iteration 3 to indicate that a shorter route has been found through node 4. Also, in iteration 3, node 5 has two alternative labels with the same distance u₅ = 90.

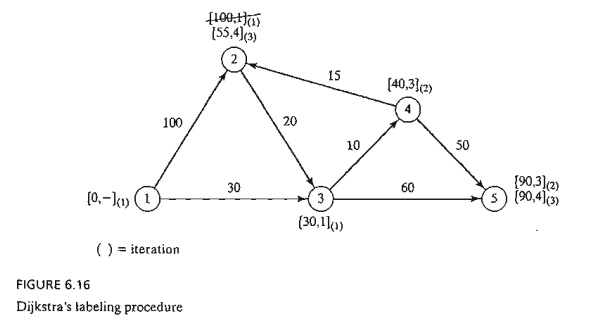
The list for iteration 3 shows that the label for node 2 is now permanent.

Iteration 4. Only node 3 can be reached from node 2. However, node 3 has a permanent label and cannot be relabeled. The new list of labels remains the same as in iteration 3 except that the label at node 2 is now permanent. This leaves node 5 as the only temporary labeL Because node 5 does not lead to other nodes, its status is convert-ed to permanent, and the process ends.

The computations of the algorithm can be carried out more easily on the network, as Figure 6.16 demonstrates.

The shortest route between nodes 1 and any other node in the network is determined by starting at the desired destination node and backtracking through the nodes using the information given by the permanent labels. For example, the following sequence determines the shortest route from node 1 to node 2:

(2) -> [55, 4] -> (4) -> [40, 3] -> (3) -> [30,1] -> (1)

Thus, the desired route is 1 -> 3 -> 4 -> 2 with a total length of 55 miles.

PROBLEM SET6.3B

1. The network in Figure 6.17 gives the distances in miles between pairs of cities 1,2, ., . , and 8. Use Dijkstra's algorithm to find the shortest route between the following cities:

a. Cities 1 and 8

b. Cities 1 and 6

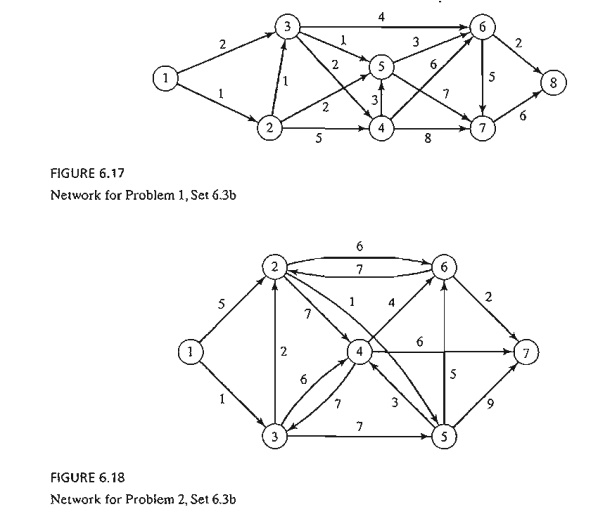
c. Cities 4 and 8

d. Cities 2 and 6

2. Use Dijkstra's algorithm to find the shortest route between node 1 and every other node in the network of Figure 6.18.

3. Use Dijkstr'a algorithm to determine the optimal solution of each of the following problems:

a. Problem 1, Set 6.3a.

b. Problem 2, Set 6.3a.

c. Problem 4, Set 6.3a.

Floyd's Algorithm. Floyd's algorithm is more general than Dijkstra's because it determines the shortest route between any two nodes in the network. The algorithm represents an n-node network as a square matrix with n rows and n columns. Entry (~j) of the matrix gives the distance d_ij from node i to node j, which is finite if i is linked directly to j, and infinite otherwise.

The idea of Floyd's algorithm is straightforward. Given three nodes i j, and k in Figure 6.19 with the connecting distances shown on the three arcs, it is shorter to reach j from i passing through k if

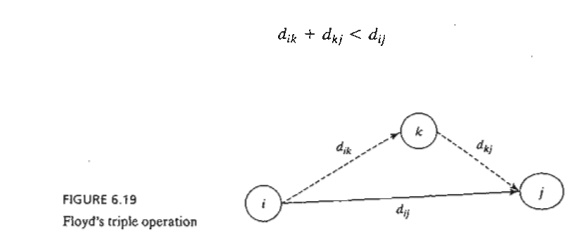
In this case, it is optimal to replace the direct route from i -> j with the indirect route i -> k -> j. This triple operation exchange is applied systematically to the network using the following steps:

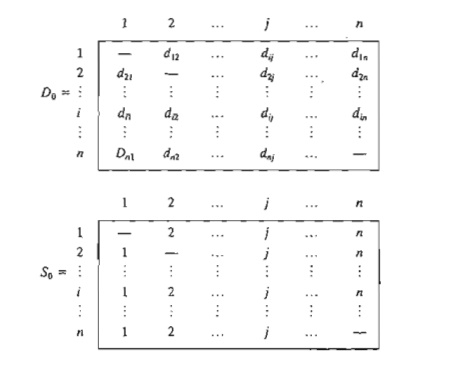
Step 0. Define the starting distance matrix D_o and node sequence matrix S_o as given below. The diagonal elements are marked with (--) to indicate that they are blocked. Set k = 1.

General step k. Define row k and column k as pivot row and pivot column. Apply the triple operation to each element d _jj in D_k - _l , for all i and j. If the condition

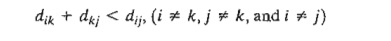
is satisfied, make the following changes:

a)     Create D_k by replacing d_ij in D_k - ₁ with d_jk  + d_kj

b)    Create Sk by replacing S_ij in S_k-l with k. Set k = k + 1. If k = n + 1, stop; else repeat step k.

Step k of the algorithm can be explained by representing D_k - ₁ as shown in Figure 6.20. Here, row k and column k define the current pivot row and column. Row i

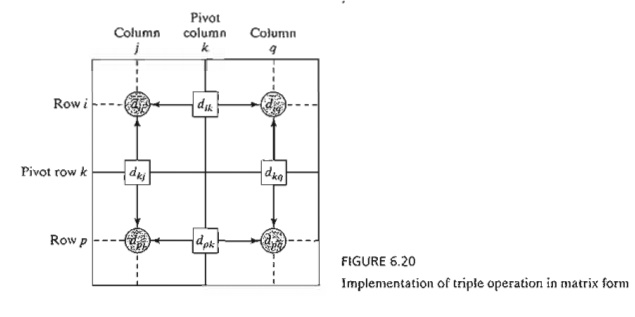
represents any of the rows 1, 2, ... , and k - 1, and row p represents any of the rows k + 1, k + 2, ... , and n. Similarly, column j represents any of the columns 1,2, ... , and k - 1, and column q represents any of the columns k + 1, k + 2, ... , and n. The triple operation can be applied as follows. If the sum of the elements on the pivot row and the pivot column (shown by squares) is smaller than the associated intersection element (shown by a circle), then it is optimal to replace the intersection distance by the sum of the pivot distances.

After n steps, we can determine the shortest route between nodes i and j from the matrices D_n and Sn using the following rules:

a)   From D_m  d_ij gives the shortest distance between nodes i and j.

b)    From Sm determine the intermediate node k = s_ij that yields the route i -> k -> j. If s_ik = k and s_kj = j, stop; all the intermediate nodes of the route have been found. Otherwise, repeat the procedure between nodes i and k, and between nodes k and j.

Example 6.3-5

For the network in Figure 6.21, find the shortest routes between every two nodes. TIle distances (in miles) are given on the arcs. Arc (3,5) is directional, so that no traffic is allowed from node 5 to node 3. All the other arcs allow two-way traffic.

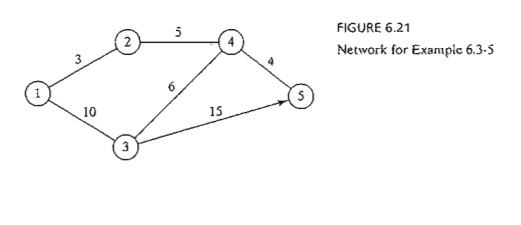
Iteration 0. The matrices D_o and S_o give the initial representation of the network. Do is sym-metrical, except that d₃₃ = ¥ because no traffic is allowed from node 5 to node 3.

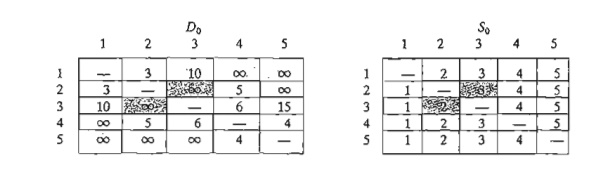
Iteration 1.

Set k = 1. The pivot row and column are shown by the lightly shaded first row and first column in the D_o-matrix. The darker cells, d₁₃ and d ₃₂ , are the only ones that can be improved by the triple operation. Thus, D₁ and SI are obtained from D_o and S_o in the following manner:

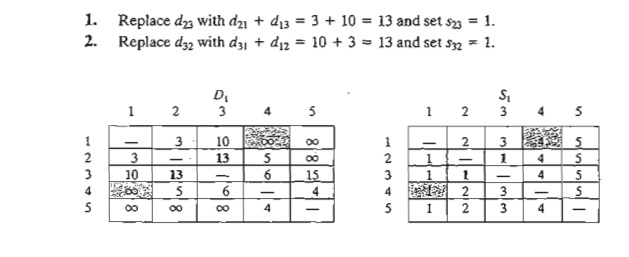
Iteration 2.

Set k = 2, as shown by the lightly shaded row and column in D₁• The tripLe oper-ation is applied to the darker cells in D₁ and S₁. The resulting changes are shown in bold in D₂ and S₂.

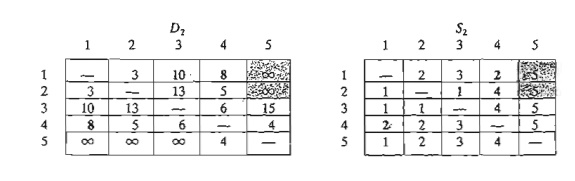
Iteration 3.

Set k = 3, as shown by the shaded row and column in D₂. The new matrices are given by D₃ and S_3.

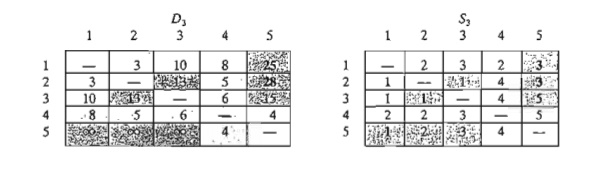
Iteration 4. Set k = 4, as shown by the shaded row and column in D₃. The new matrices are given by D₄ and S₄.

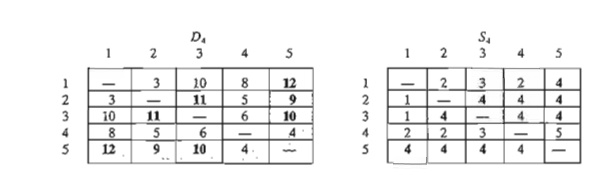
Iteration 5. Set k = 5, as shown by the shaded row and column in D₄. No further improvements are possible in this iteration.

The final matrices D₄ and S₄ contain all the information needed to determine the shortest route between any two nodes in the network. For example, from D₄, the shortest distance from node 1 to node 5 is d _l5 = 12 miles. To determine the associated route, recall that a segment (i, j) represents a direct link only if s_ij = j. Otherwise, i and j are linked through at least one other intermediate node. Because s_ij = 4 != 5, the route is initially given as 1 -> 4 -> 5. Now, because s₁₄ = 2 != 4, the segment'(I,4) is not a direct link, and 1 -> 4 is replaced with 1 -> 2 -> 4, and the route 1 -> 4 -> 5 now becomes 1 -> 2 -> 4 -> 5. Next, because s₁₂ = 2, s₂₄ = 4, and s₄₅ = 5, no further "dissecting" is needed, and 1 -> 2 -> 4 -> 5 defines the shortest route.

PROBLEM SET 6.3C

1. In Example 6.3-5, use Floyd's algorithm to determine the shortest routes between each of the following pairs of nodes:

*(a)       From node 5 to node 1.

(b)     From node 3 to node 5.

(c) From node 5 to node 3.

(d) From node 5 to node 2.

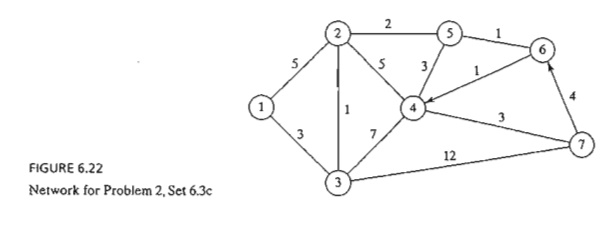
2. Apply Floyd's algorithm to the network in Figure 6.22. Arcs (7,6) and (6,4) are unidirectional, and all the distances are in miles. Determine the shortest route between the following pairs of nodes:

(a) From node 1 to node 7.

(b) From node 7 to node 1.

(c) From node 6 to node 7.

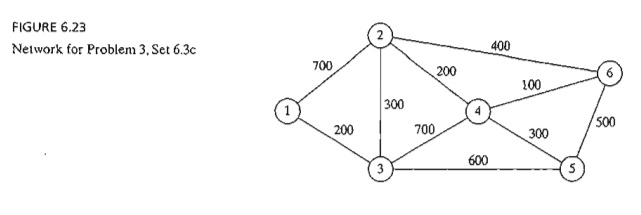
3. The Tell-All mobile-phone company services six geographical areas. The satellite distances (in miles) among the six areas are given in Figure 6.23. Tell-All needs to determine the most efficient message routes that should be established between each two areas in the network.

*4. Six kids, Joe, Kay, Jim, Bob, Rae, and Kim, playa variation of hide and seek. The hiding place of a child is known only to a select few of the other children. A child is then paired with another with the objective of finding the partner's hiding place. This may be achieved through a chain of other kids who eventually will lead to discovering where the designated child is hiding. For example, suppose that Joe needs to find Kim and that Joe knows where Jim is hiding, who in turn knows where Kim is. Thus, Joe can find Kim by first finding Jim, who in turn will lead Joe to Kim. The following list provides the where-abouts of the children:

Joe knows the hiding places of Bob and Kim.

Kay knows the hiding places of Bob, Jim, and Rae.

Jim and Bob each know the hiding place of Kay only.

Rae knows where Kim is hiding.

Kim knows where Joe and Bob are hiding.

Devise a plan for each child to find every other child through the smallest number of contacts. What is the largest number of contacts?