Resolution of vectors and rectangular components

Resolution of vectors and rectangular components

A vector directed at an angle with the co-ordinate axis, can be resolved into its components along the axes. This process of splitting a vector into its components is known as resolution of a vector.

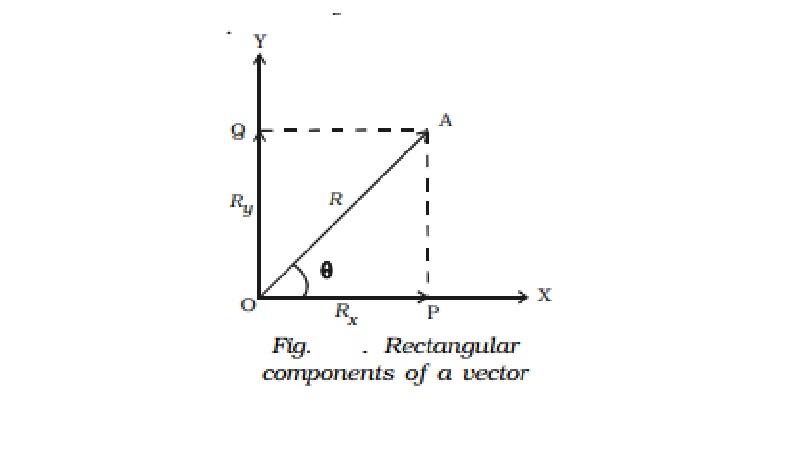
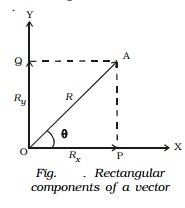
Consider a vector R = Vector( OA) making an angle θ with X - axis. The vector R can be resolved into two components along X - axis and Y-axis respectively. Draw two perpendiculars from A to X and Y axes respectively. The intercepts on these axes are called the scalar components R_x and R_y.

Then, OP is R^x, which is the  magnitude of x component of Vector R and OQ is R_y, which is the magnitude of y component of Vector  R .

From ∆ OPA,

cos θ = OP/OA = R_x/R  (or) R_x=Rcos θ

sin θ = OQ/OA = R_y/R  (or) R_y=Rsin θ

R2 = R_x² + R_y²

Also, Vector R can be expressed as Vector R = R_xi + R_yj where i and j are unit vectors.

In terms of R_x and R_y , θ can be expressed as θ = tan⁻¹ [R_y/R_x]

Scalar and vector quantities

A study of motion will involve the introduction of a variety of quantities, which are used to describe the physical world. Examples of such quantities are distance, displacement, speed, velocity, acceleration, mass, momentum, energy, work, power etc. All these quantities can be divided into two categories ? scalars and vectors.

The scalar quantities have magnitude only. It is denoted by a number and unit. Examples : length, mass, time, speed, work, energy,

temperature etc. Scalars of the same kind can be added, subtracted, multiplied or divided by ordinary laws.

The vector quantities have both magnitude and direction. Examples: displacement, velocity, acceleration, force, weight, momentum, etc.