Definition, Theorem, Formulas, Solved Example Problems | Inverse of a Non-Singular Square Matrix - Properties of inverses of matrices | 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Chapter: 12th Mathematics : UNIT 1 : Applications of Matrices and Determinants
Properties of inverses of matrices
Properties of inverses of matrices
We state and prove some theorems on non-singular matrices.
Theorem 1.4
If A is
non-singular, then
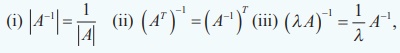
, where λ is a
non-zero scalar.
Proof
Let A be non-singular. Then |A| ≠0 and A−1 exists. By
definition,
Theorem 1.5 (Left Cancellation Law)
Let A, B, and C be square matrices of order
n. If A is non-singular and AB = AC, then B = C.
Proof
Since A is non-singular, A−1 exists and AA−1 = A−1 A = In .
Taking AB = AC and pre-multiplying both sides by A−1, we get A−1 ( AB) = A−1 ( AC). By
using the associative property of matrix multiplication and property of inverse
matrix, we get B = C.
Theorem1.6 (Right Cancellation Law)
Let A, B, and C be square matrices of order
n. If A is non-singular and BA = CA, then B = C.
Proof
Since A is non-singular, A−1 exists and AA−1 = A−1 A = In .
Taking BA = CA and post-multiplying both sides by A−1, we get (BA) A−1 = (CA) A−1. By using the
associative property of matrix multiplication and property of inverse matrix,
we get B = C.
Note
If A is singular and AB = AC or BA = CA, then B and
C need not be equal. For instance, consider the following matrices:
We note that |A| = 0 and AB = AC ; . but B ≠C
Theorem
1.7 (Reversal Law for Inverses)
If A and B are
non-singular matrices of the same order, then the product AB is also
non-singular and ( AB)−1 = B−1 A−1.
Proof
Assume that A and
B are non-singular matrices of same order n. Then,| A | ≠0, | B | ≠0, both A−1 and B−1 exist and they are of
order n. The products AB and B−1 A−1 can be found and they
are also of order n. Using the product rule for determinants, we get |AB|
=| A || B |≠0. So, AB is
non-singular and
( AB)(B-1 A-1 ) = ( A(BB-1 )) A-1
= ( AIn ) A-1 = AA-1 = In ;
(B-1 A-1 )( AB) = (B-1 ( A-1
A))B = (B-1In )B = B-1B = In .
Hence ( AB)−1 = B−1 A−1.
Theorem
1.8 (Law of Double Inverse)
If A is
non-singular, then A−1 is also non-singular and ( A−1 )−1 = A.
Proof
Assume that A is non-singular. Then |A | ≠0, and A−1 exists.
Now, |A-1| = 1/|A| ≠0
⇒ A-1 is also non-singular, and AA-1
= A-1A = I
Now, A-1A = I ⇒ (AA-1)-1 = I ⇒ (A-1)-1
A-1 = I.
Post-multiplying
by A on both sides of equation (1), we get (A-1)-1
=A.
Theorem 1.9
If A is a non-singular square matrix of order n ,
then
Proof
Since A is a non-singular square matrix, we have |A| ≠0 and so, we get
Note
If
A is a non-singular matrix of order
3, then, |A | ≠0 . By theorem 1.9 (ii), we get |adjA| = | A|2 and
so, | adj A | is positive. Then, we get |A| = ± √|adjA| .
So,
we get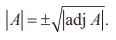 
Further,
by property (iii), we get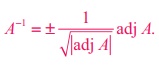 
Hence,
if A is a non-singular matrix of order 3, then we get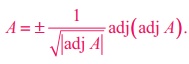 
Example 1.4
If A is a non-singular matrix of odd order, prove that |adj
A| is positive.
Solution
Let A be a non-singular matrix of order 2m + 1 , where m = 0,1, 2,
.. . . Then, we get |A| ≠0 and, by theorem 1.9 (ii), we have |adj A| = |A|(2m+1)-1
= |A|2m
Since |A|2m is always positive, we get that |adj A| is
positive.
Example 1.5
Find a matrix A if adj( A) =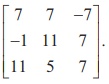 
Solution
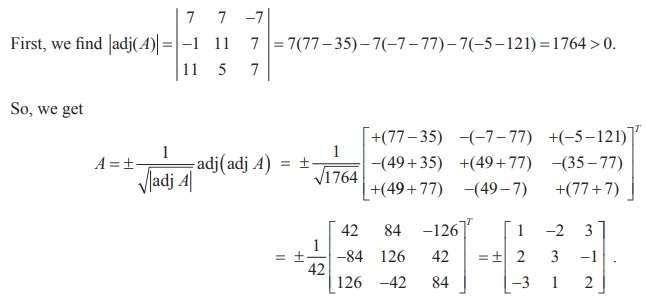
Example 1.6
If adj A =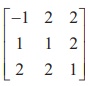
find A−1.
Solution
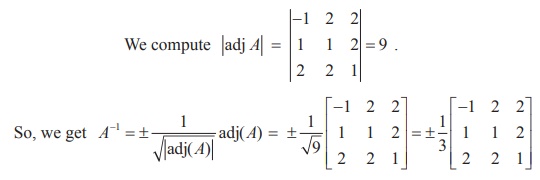
Example1.7
If A is symmetric, prove that adj A is also
symmetric.
Solution
Suppose A is symmetric. Then, AT = A and so, by theorem
1.9 (vi), we get
adj (AT) = (adj A) T ⇒ adj A =
(adj A)T ⇒ adj A is symmetric
Theorem
1.10
If A and B are
any two non-singular square matrices of order n , then
adj( AB) = (adj B)(adj A).
Proof
Replacing A by AB in
adj(A) = |A|A−1 , we get
adj(AB) = |AB| (AB)-1 = (| B | B-1) (| A | A-1)
= adj(B) adj(A)
Example 1.8
Verify the property ( AT )−1 = ( A−1 )T with A =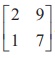 
.
Solution
For the given A, we get |A |= (2) (7) - (9)(1) = 14 − 9 = 5 .
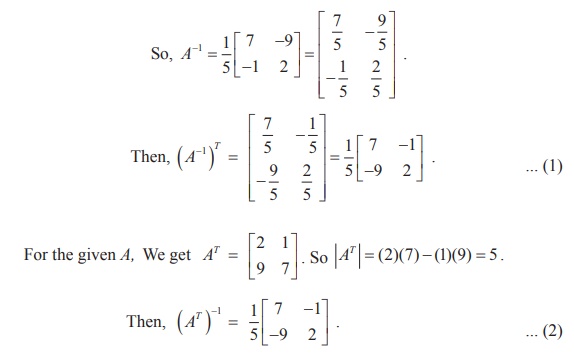
From
(1) and (2), we get (A-1) = (AT)-1. Thus, we
have verified the given property.
Example 1.9
Verify ( AB)−1 = B−1 A−1 with 
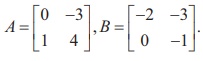
Solution
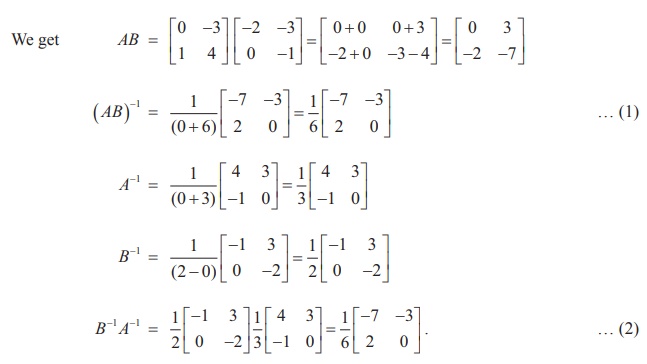
As
the matrices in (1) and (2) are same, (AB) −1 = B-1 A-1
is verified.
Example 1.10
If A =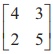 
, find x and y
such that A2 + xA + yI2=O2, Hence, find A−1.
Solution
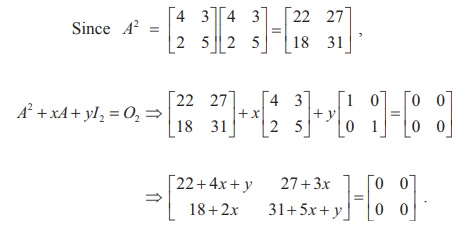
So,
we get 22 + 4x + y =0, 31+5x+y=0, 27+3x=0 and 18+2x=0
Hence
x = −9 and y =14.Then, we get A2 - 9A + 14I2 = O2
Post-multiplying
this equation by A−1 , we get A – 9I2 + 14A-1
= O2. Hence, we get
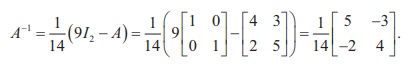
Related Topics