Chapter: 10th Mathematics : UNIT 3 : Algebra
Properties of Matrix Addition and Scalar Multiplication
Properties of Matrix Addition and Scalar
Multiplication
Let A, B, C be m ×n matrices and p and
q be two non-zero scalars (numbers). Then we have the following
properties.
(i) A + B = B +
A [Commutative property of matrix addition]
(ii) A + (B +
C) = (A + B) +C [Associative
property of matrix addition]
(iii) ( pq)A = p(qA)
[Associative property of scalar multiplication]
(iv) IA=A [Scalar Identity
property where I is the unit matrix]
(v) p(A + B)
= pA + pB [Distributive property of scalar and two matrices]
(vi) ( p + q )A = pA +qA
[Distributive property of two scalars with a matrix]
Additive Identity
The null matrix or zero matrix is the identity for matrix addition.
Let A be any matrix.
Then, A + O = O + A = A where O
is the null matrix or zero matrix of same order as that of A
Additive Inverse
If A be any given matrix then –A is the additive inverse of A.
In fact we have A + (−A) = (−A) + A = O
Example 3.62
Find the value of a, b, c, d, x, y from the following
matrix equation.
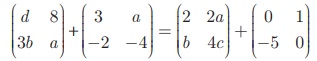
Solution
First, we add the two matrices on both left, right hand sides to
get
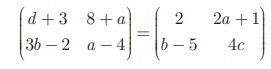
Equating the corresponding elements of the two matrices, we have
d + 3 = 2 gives d = –1
8 + a = 2a + 1 gives a = 7
3b − 2 = b – 5 gives b = -3/4
Substituting a = 7 in a − 4 = 4c gives c
= 3/4
Therefore, a = 7, b = − 3/2, c = 3/4, d
= –1.
Example 3.63
If 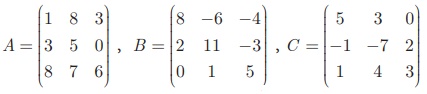
compute the following : (i) 3A + 2B – C (ii) 1/2 A -3/2 B
Solution
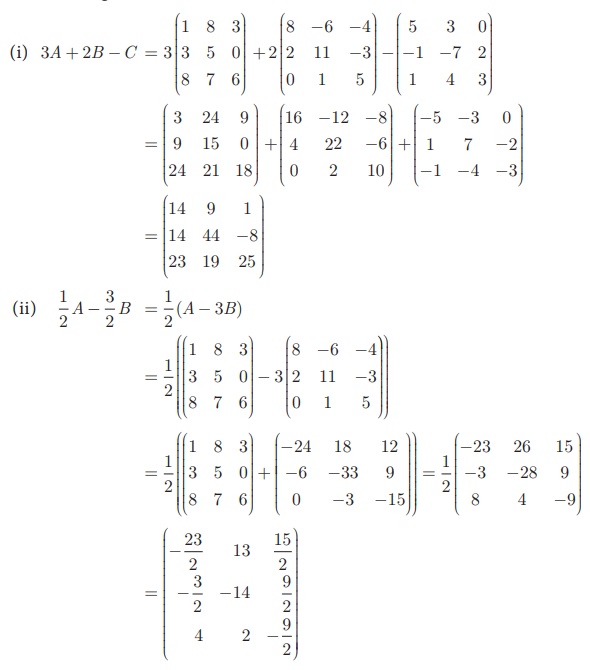
Related Topics