Properties of Discrete Fourier Transform(DFT)

PROPERTIES OF DFT

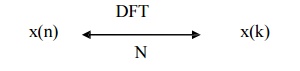
1.     Periodicity

Let x(n) and x(k) be the DFT pair then if

x(n+N) = x(n)                                                                                     for all n then

X(k+N) = X(k)                                                                                   for all k

Thus periodic sequence xp(n) can be given as

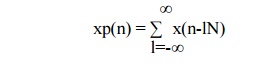
2.     Linearity

The linearity property states that if

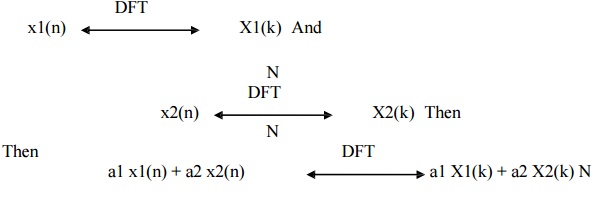
DFT of linear combination of two or more signals is equal to the same linear combination of DFT of individual signals.

3.     Circular Symmetries of a sequence

 A) A sequence is said to be circularly even if it is symmetric about the point zero on the circle. Thus X(N-n) = x(n)

 B) A sequence is said to be circularly odd if it is anti symmetric about the point zero on the circle. Thus X(N-n) = - x(n)

 C) A circularly folded sequence is represented as x((-n))N and given by x((-n))N = x(N-n).

 D) Anticlockwise direction gives delayed sequence and clockwise direction gives advance sequence.

Thus delayed or advances sequence x`(n) is related to x(n) by the circular shift.

4.     Symmetry Property of a sequence

A.    Symmetry property for real valued x(n) i.e xI(n)=0

This property states that if x(n) is real then X(N-k) = X^*(k)=X(-k)

B) Real and even sequence x(n) i.e xI(n)=0 & XI(K)=0

This property states that if the sequence is real and even x(n)= x(N-n) then DFT becomes N-1

C) Real and odd sequence x(n) i.e xI(n)=0 & XR(K)=0

This property states that if the sequence is real and odd x(n)=-x(N-n) then DFT becomes N-1

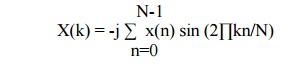
D) Pure Imaginary x(n) i.e xR(n)=0

This property states that if the sequence is purely imaginary x(n)=j XI(n) then DFT becomes

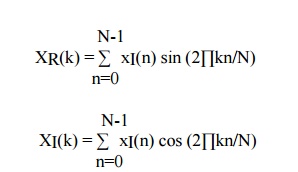
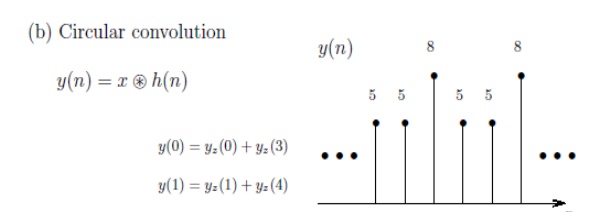
5.     Circular Convolution

The Circular Convolution property states that if

It means that circular convolution of x1(n) & x2(n) is equal to multiplication of their DFT s. Thus circular convolution of two periodic discrete signal with period N is given by

Multiplication of two sequences in time domain is called as Linear convolution while Multiplication of two sequences in frequency domain is called as circular convolution. Results of both are totally different but are related with each other.

There are two different methods are used to calculate circular convolution

Graphical representation form

Matrix approach

DIFFERENCE BETWEEN LINEAR CONVOLUTION & CIRCULAR CONVOLUTION

Linear Convolution

1. In case of convolution two signal sequences input signal x(n) and impulse response h(n) given by the same system, output y(n) is calculated

2. Multiplication of two sequences in time domain is called as Linear convolution

3. Linear Convolution is given by the equation y(n) = x(n) * h(n) & calculated as

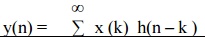
4. Linear Convolution of two signals returns N-1 elements where N is sum of elements in both sequences.

Circular Convolution

1. Multiplication of two DFT s is called as circular convolution.

2. Multiplication  of  two  sequences in frequency domain is called as circular convolution.

3. Circular Convolution is calculated as 

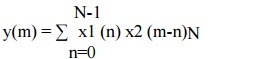
4. Circular convolution returns same number of elements that of two signals.

Q) The two sequences x1(n)={2,1,2,1} & x2(n)={1,2,3,4}. Find out the sequence x3(m) which is equal to circular convolution of two sequences. Ans: X3(m)={14,16,14,16}

Q) x1(n)={1,1,1,1,-1,-1,- 1,-1} & x2(n)={0,1,2,3,4,3,2,1}. Find out the sequence x3(m) which is equal to circular convolution of two sequences. Ans: X3(m)={-4,-8,-8,-4,4,8,8,4}

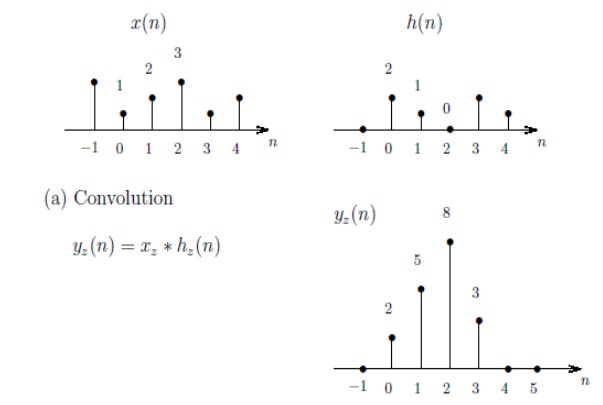
Q) Perform Linear Convolution of x(n)={1,2} & h(n)={2,1} using DFT & IDFT.

Q) Perform Linear Convolution of x(n)={1,2,2,1} & h(n)={1,2,3} using 8 Pt DFT & IDFT.

DIFFERENCE BETWEEN LINEAR CONVOLUTION & CIRCULAR CONVOLUTION

6.     Multiplication

The Multiplication property states that if

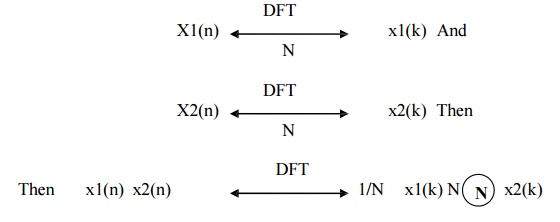
It means that multiplication of two sequences in time domain results in circular convolution of their DFT s in frequency domain.

7.     Time reversal of a sequence

The Time reversal property states that if

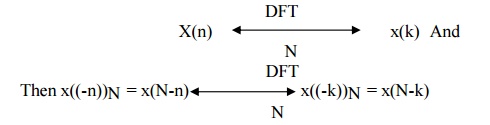
It means that the sequence is circularly folded its DFT is also circularly folded.

8.     Circular Time shift

The Circular Time shift states that if

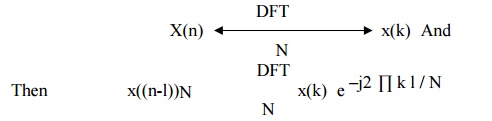
Thus shifting the sequence circularly by „l  samples is equivalent to multiplying its DFT by _e –j2 ∏ k l / N

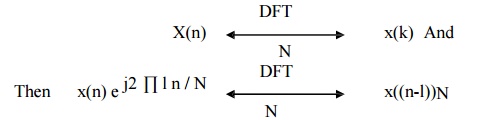
9.     Circular frequency shift

The Circular frequency shift states that if

Thus shifting the frequency components of DFT circularly is equivalent to multiplying its time domain sequence by e ^{–j2 ∏ k l / N}

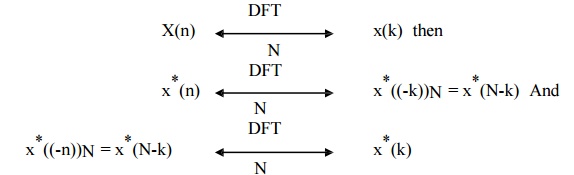
10.     Complex conjugate property

The Complex conjugate property states that if

11.     Circular Correlation

The Complex correlation property states

Here rxy(l) is circular cross correlation which is given as

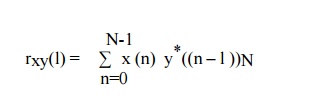
This means multiplication of DFT of one sequence and conjugate DFT of another sequence is equivalent to circular cross-correlation of these sequences in time domain.

12.Parseval’sTheorem

The Parseval s theorem states

This equation give energy of finite duration sequence in terms of its frequency components.