Solved Example Problems | Trigonometry | Mathematics - Problems involving Angle of Elevation | 10th Mathematics : UNIT 6 : Trigonometry
Chapter: 10th Mathematics : UNIT 6 : Trigonometry
Problems involving Angle of Elevation
Heights and Distances
In this section, we will see how trigonometry is used for finding
the heights and distances of various objects without actually measuring them.
For example, the height of a tower, mountain, building or tree, distance of a
ship from a light house, width of a river, etc. can be determined by using
knowledge of trigonometry. The process of finding Heights and Distances is the best example of
applying trigonometry in real-life situations. We would explain these
applications through some examples. Before studying methods to find heights and
distances, we should understand some basic definitions.
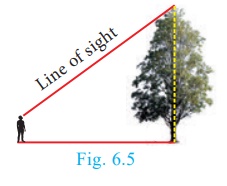
Line of Sight
The line of sight is the line drawn from the eye of an observer to the point in the
object viewed by the observer.
Theodolite
Theodolite is an instrument which is used in measuring the angle
between an object and the eye of the observer. A theodolite consists of two
graduated wheels placed at right angles to each other and a telescope. The
wheels are used for the measurement of horizontal and vertical angles. The
angle to the desired point is measured by positioning the telescope towards
that point. The angle can be read on the telescope scale.

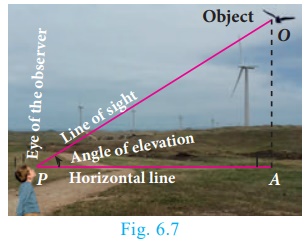
Angle of Elevation
The angle of elevation is an angle formed by the line of sight with the horizontal when the point being
viewed is above the horizontal level.
That is, the case when we raise our head to look at the object. (see Fig. 6.7)
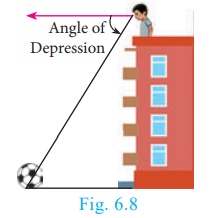
Angle of Depression
The angle of depression is an angle formed by the line of sight with the horizontal when the point is below the horizontal level.
That is, the case when we lower our head to look at the point being viewed.
(see Fig. 6.8)
Clinometer
The angle of elevation and depression are usually measured by a
device called clinometer.

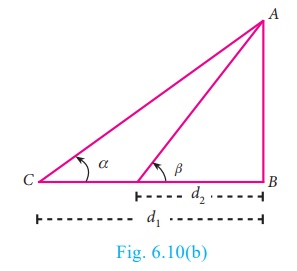
Note
·
From
a given point, when height of a object increases the angle of elevation
increases.
If h1
> h2 then α > β
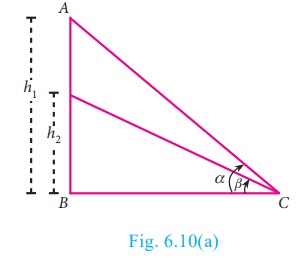
·
The
angle of elevation increases as we move towards the foot of the vertical object
like tower or building.
If
d2 < d2 then β > α
Problems involving Angle of Elevation
In this section, we try to solve problems when Angle of elevation
are given.
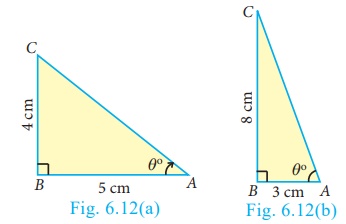
Example 6.18
Calculate
the size of ∠BAC
in the given triangles.
Solution
(i) In right triangle ABC [see Fig.6.12(a)]
tan θ = opposite side / adjacent side = 4/5
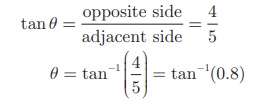
θ = 38.7°
(since tan 38.7° = 0.8011)
∠BAC = 38.7°
(ii) In right triangle ABC [see Fig.6.12(b)]
tan θ = 8/3
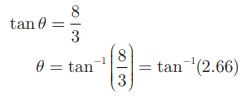
θ = 69.4° (since tan 69.4°
= 2.6604)
∠BAC = 69.4°
Example 6.19
A tower stands vertically on the ground. From a point on the
ground,
which is 48 m away from
the foot of the tower, the angle of elevation of the top of the tower is 30° .
Find the height of the tower.
Solution
Let PQ be the height of the tower.
Take PQ = h and QR is the distance
between the tower and the point R. In right triangle PQR, ∠PRQ = 30°
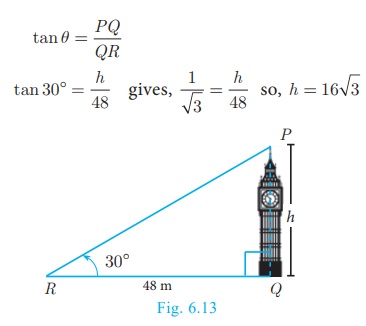
Therefore the height of the tower is 16√3 m
Example 6.20
A kite is flying at a height of 75 m above the ground. The
string attached to the kite is temporarily tied to a point on the ground. The
inclination of the string with the ground is 60° . Find the length of the
string, assuming that there is no slack in the string.
Solution
Let AB be the height of the kite above the ground. Then, AB = 75.
Let AC be the length of the string.
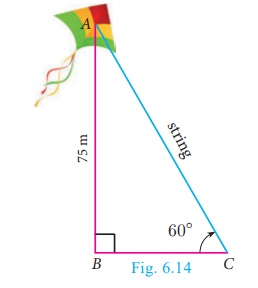
In right triangle ABC, ∠ACB = 60°
sin θ = AB/AC
sin 60° = 75/AC
gives √3/2 = 75/AC so AC = 150/√3 = 50√3 m
Hence, the length of the string is 50√3 m.
Example 6.21
Two ships are sailing in the sea on either sides of a lighthouse.
The angle of elevation of
the top of the lighthouse as observed from the ships are 30° and 45°
respectively. If the lighthouse is 200 m high, find the distance between the
two ships. (√3=1.732)
Solution
Let AB be the lighthouse. Let C and D be the positions of the two
ships.

Then, AB = 200 m.
∠ACB = 30° ,
∠ADB = 45°
In right triangle BAC, tan 30° = AB/AC
1/√3 = 200/AC gives AC = 200√3 ...(1)
In right triangle BAD, tan 45° = AB/AD
1 = 200/AD
gives AD = 200 ...(2)
Now, CD = AC + AD = 200√3 + 200 [by (1) and (2)]
CD = 200(√3 + 1)
= 200 × 2. 732 = 546.4
Distance between two ships is 546.4 m.
Example 6.22
From a point on the ground, the angles of elevation of the bottom
and top
of a tower fixed at the
top of a 30 m high building are 45° and 60° respectively. Find the height of
the tower. (√3=1.732)
Solution
Let AC be the height of the tower.

Let AB be the height of the building. Then, AC = h
metres, AB = 30 m
In right triangle CBP, ∠CPB = 60°
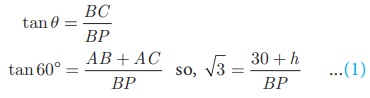
In right triangle ABP, ∠APB = 45°
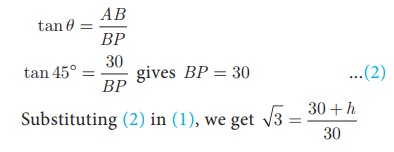
h = − 30(√3 - 1) = 30 (1.732
– 1) = 30(0.732) = 21.96
Hence, the height of the tower is 21.96 m.
Example 6.23
A TV tower stands vertically on a bank of a canal. The tower is
watched
from a point on the
other bank directly opposite to it. The angle of elevation of the top of the
tower is 58° . From another point 20
m away from this point on the line joining this point to the foot of the tower,
the angle of elevation of the top of the tower is 30° . Find the height of the tower and the width of
the canal. (tan 58° = 1.6003)
Solution
Let AB be the height of the TV tower.
CD = 20 m.
Let BC be the width of the canal.

AB = 17.99
Hence, the height of the tower is 17.99 m and the width of the canal is 11.24 m.
Example 6.24
An aeroplane sets off from G on a bearing of 24° towards H, a point 250 km away. At H it changes course and heads towards J
on a bearing of 55° and a distance of 180 km away.
(i) How far is H to the North of G?
(ii) How far is H to the East of G?
(iii) How far is J to the North of H?
(iv) How far is J to the East of H?

Solution
(i) In right triangle GOH, cos 24° = OG/GH
0.9135 = OG/250 ; OG= 228.38 km
Distance of H to the North of G = 228.38 km
(ii) In right triangle GOH,
sin 24° = OH/GH
0. 4067 = OH/250 ; OH= 101. 68
Distance of H to the East of G = 101. 68 km
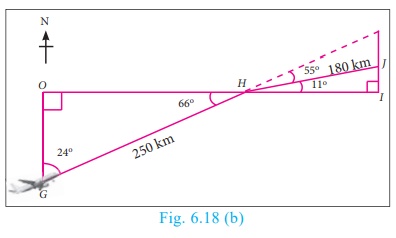
(iii) In right triangle HIJ,
sin 11° = IJ/HJ
0. 1908 = IJ/180 ; IJ = 34. 34 km
Distance of J to the North of H = 34. 34 km
(iv) In right triangle HIJ,
cos 11° = HI/HJ
0. 9816 = HI / 180 ; HI = 176. 69 km
Distance of J to the East of H = 176. 69 km
Example 6.25
Two trees are standing on flat ground. The angle of elevation of
the top of
both the trees from a
point X on the ground is 40° . If the horizontal distance between X
and the smaller tree is 8 m and the distance of the top of the two trees is 20
m, calculate
(i) the distance between the point X and the top of the
smaller tree.
(ii) the horizontal distance between the two trees. (cos 40° = 0. 7660)
Solution
Let AB be the height of the bigger tree and CD be the height of the
smaller tree and X is the point on the ground.

(i) In right triangle XCD, cos 40°= CX/XD
XD = 8 / 0.7660 = 10. 44 m
Therefore the distance between X and top of the smaller
tree = XD = 10.44 m
(ii) In right triangle XAB,
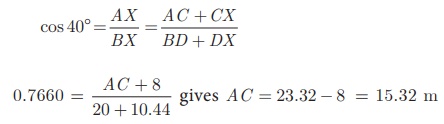
Therefore the horizontal distance between two trees = AC =
15.32 m
Related Topics