Multivalued Dependency and Fourth Normal Form

Multivalued Dependency and Fourth Normal Form

So far we have discussed the concept of functional dependency, which is by far the most important type of dependency in relational database design theory, and normal forms based on functional dependencies. However, in many cases relations have constraints that cannot be specified as functional dependencies. In this section, we discuss the concept of multivalued dependency (MVD) and define fourth normal form, which is based on this dependency. A more formal discussion of MVDs and their properties is deferred to Chapter 16. Multivalued dependencies are a consequence of first normal form (1NF) (see Section 15.3.4), which disallows an attribute in a tuple to have a set of values, and the accompanying process of converting an unnormalized relation into 1NF. If we have two or more multivalued independent attributes in the same relation schema, we get into a problem of having to repeat every value of one of the attributes with every value of the other attribute to keep the relation state consistent and to maintain the independence among the attributes involved. This constraint is specified by a multivalued dependency.

For example, consider the relation EMP shown in Figure 15.15(a). A tuple in this EMP relation represents the fact that an employee whose name is Ename works on the project whose name is Pname and has a dependent whose name is Dname. An employee may work on several projects and may have several dependents, and the employee’s projects and dependents are independent of one another. To keep the relation state consistent, and to avoid any spurious relationship between the two independent attributes, we must have a separate tuple to represent every combina-tion of an employee’s dependent and an employee’s project. This constraint is spec

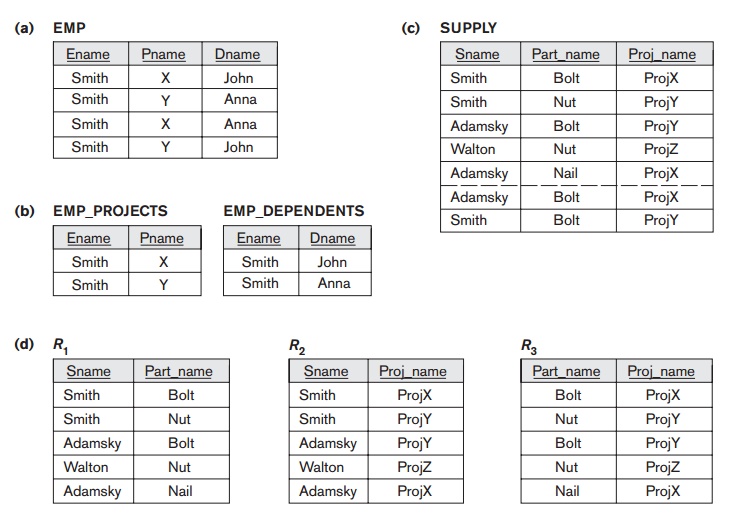
ified as a multivalued dependency on the EMP relation, which we define in this section. Informally, whenever two independent 1:N relationships A:B and A:C are mixed in the same relation, R(A, B, C), an MVD may arise.

Formal Definition of Multivalued Dependency

Definition. A multivalued dependency X →→ Y specified on relation schema R, where X and Y are both subsets of R, specifies the following constraint on any relation state r of R: If two tuples t₁ and t₂ exist in r such that t₁[X] = t₂[X], then

two tuples t₃ and t₄ should also exist in r with the following properties,¹⁵ where we use Z to denote (R – (X ∪ Y)):¹⁶

        t₃[X] = t₄[X] = t₁[X] = t₂[X].

        t₃[Y] = t₁[Y] and t₄[Y] = t₂[Y].

        t₃[Z] = t₂[Z] and t₄[Z] = t₁[Z].

Whenever X →→ Y holds, we say that X multidetermines Y. Because of the symme-try in the definition, whenever X →→ Y holds in R, so does X →→ Z. Hence, X →→ Y implies X →→ Z, and therefore it is sometimes written as X →→ Y|Z.

An MVD X →→ Y in R is called a trivial MVD if (a) Y is a subset of X, or (b) X ∪ Y = R. For example, the relation EMP_PROJECTS in Figure 15.15(b) has the trivial MVD Ename →→ Pname. An MVD that satisfies neither (a) nor (b) is called a nontrivial MVD. A trivial MVD will hold in any relation state r of R; it is called triv-ial because it does not specify any significant or meaningful constraint on R.

If we have a nontrivial MVD in a relation, we may have to repeat values redundantly in the tuples. In the EMP relation of Figure 15.15(a), the values ‘X’ and ‘Y’ of Pname are repeated with each value of Dname (or, by symmetry, the values ‘John’ and ‘Anna’ of Dname are repeated with each value of Pname). This redundancy is clearly undesirable. However, the EMP schema is in BCNF because no functional dependencies hold in EMP. Therefore, we need to define a fourth normal form that is stronger than BCNF and disallows relation schemas such as EMP. Notice that relations con-taining nontrivial MVDs tend to be all-key relations—that is, their key is all their attributes taken together. Furthermore, it is rare that such all-key relations with a combinatorial occurrence of repeated values would be designed in practice. However, recognition of MVDs as a potential problematic dependency is essential in relational design.

We now present the definition of fourth normal form (4NF), which is violated when a relation has undesirable multivalued dependencies, and hence can be used to identify and decompose such relations.

Definition. A relation schema R is in 4NF with respect to a set of dependencies F (that includes functional dependencies and multivalued dependencies) if, for every nontrivial multivalued dependency X →→ Y in F⁺¹⁷ X is a superkey for R.

We can state the following points:

        An all-key relation is always in BCNF since it has no FDs.

        An all-key relation such as the EMP relation in Figure 15.15(a), which has no FDs but has the MVD Ename →→ Pname | Dname, is not in 4NF.

        A relation that is not in 4NF due to a nontrivial MVD must be decomposed to convert it into a set of relations in 4NF.

        The decomposition removes the redundancy caused by the MVD.

The process of normalizing a relation involving the nontrivial MVDs that is not in 4NF consists of decomposing it so that each MVD is represented by a separate rela-tion where it becomes a trivial MVD. Consider the EMP relation in Figure 15.15(a). EMP is not in 4NF because in the nontrivial MVDs Ename →→ Pname and Ename

        Dname, and Ename is not a superkey of EMP. We decompose EMP into EMP_PROJECTS and EMP_DEPENDENTS, shown in Figure 15.15(b). Both EMP_PROJECTS and EMP_DEPENDENTS are in 4NF, because the MVDs Ename         Pname in EMP_PROJECTS and Ename →→ Dname in EMP_DEPENDENTS are trivial  MVDs. No  other  nontrivial  MVDs  hold  in  either  EMP_PROJECTS or EMP_DEPENDENTS. No FDs hold in these relation schemas either.